
The Challenge of Underfitting and Overfitting in Machine Learning
Kohtaat väistämättä tämän kysymyksen datatieteilijän haastattelussa:
Voitko selittää, mitä on ali- ja ylisovittaminen koneoppimisen kontekstissa? Kuvaile se tavalla, jonka myös ei-tekninen henkilö ymmärtää.
Kykysi selittää tämä ei-teknisellä ja helposti ymmärrettävällä tavalla saattaa hyvinkin ratkaista soveltuvuutesi datatieteilijän tehtävään!
Työskennellessämme koneoppimisprojektin parissa kohtaamme usein tilanteita, joissa törmäämme odottamattomiin suorituskyky- tai virheprosenttieroihin harjoittelujoukon ja testijoukon välillä (kuten alla). Miten malli voi suoriutua niin hyvin harjoitusjoukossa ja yhtä huonosti testijoukossa?

Tämä tapahtuu hyvin usein aina, kun työskentelen puupohjaisten ennustemallien kanssa. Algoritmien toimintatavan vuoksi voitte kuvitella, kuinka hankalaa on välttää ylisovittamisen ansaan joutumista!
Myös se voi olla melko pelottavaa, kun emme pysty löytämään perimmäistä syytä siihen, miksi ennustemallimme käyttäytyy näin poikkeavasti.
Tässä on omakohtainen kokemukseni – jos kysyt keneltä tahansa kokeneelta tietojenkäsittelytieteilijältä tästä, he alkavat tyypillisesti puhua jostain joukosta hienoja termejä, kuten ylisovittaminen, alisovittaminen, harhaisuus (engl. Bias) ja varianssi. Mutta vähän kukaan puhuu intuitiosta näiden koneoppimisen käsitteiden takana. Korjataanpa tämä, eikö niin?
Katsotaanpa esimerkki Underfitting vs. Overfittingin ymmärtämiseksi
Haluan selittää nämä käsitteet todellisen esimerkin avulla. Monet puhuvat teoreettisesta näkökulmasta, mutta minusta se ei riitä – meidän on havainnollistettava, miten ali- ja ylisovitus todellisuudessa toimivat.
Palaamme siis takaisin opiskeluaikoihimme.

Harkitaan matematiikan kurssia, jossa on 3 opiskelijaa ja professori.
Missä tahansa luokkahuoneessa opiskelijat voidaan jakaa karkeasti ottaen kolmeen luokkaan. Puhumme heistä yksi kerrallaan.

Sitotaan, että oppilas A muistuttaa oppilasta, joka ei pidä matematiikasta. Hän ei ole kiinnostunut siitä, mitä tunnilla opetetaan, eikä siksi kiinnitä paljon huomiota professoriin ja hänen opettamaansa sisältöön.

Katsotaanpa opiskelijaa B. Hän on kilpailuhenkinen opiskelija, joka keskittyy ulkoa opettamaan jokaisen tunnilla opetettavan kysymyksen sen sijaan, että keskittyisi keskeisiin käsitteisiin. Periaatteessa häntä ei kiinnosta ongelmanratkaisutavan oppiminen.

Viimeiseksi meillä on ihanneoppilas C. Hän on puhtaasti kiinnostunut oppimaan keskeiset käsitteet ja ongelmanratkaisutavan matematiikan tunnilla sen sijaan, että hän vain muistaisi esitetyt ratkaisut ulkoa.

Me kaikki tiedämme kokemuksesta, mitä luokkahuoneessa tapahtuu. Professori pitää ensin luennot ja opettaa opiskelijoille ongelmat ja niiden ratkaisemisen. Päivän päätteeksi professori yksinkertaisesti tekee kokeen, joka perustuu siihen, mitä hän opetti tunnilla.
Esteenä ovat lukukauden3 kokeet, jotka koulu määrää. Siinä tulee uusia kysymyksiä (näkemättömiä tietoja). Opiskelijat eivät ole nähneet näitä kysymyksiä aiemmin eivätkä todellakaan ole ratkaisseet niitä luokassa. Kuulostaako tutulta?
Keskustellaan siis siitä, mitä tapahtuu, kun opettaja tekee luokkakokeen päivän päätteeksi:

- Opiskelija A, joka oli hajamielinen omassa maailmassaan, yksinkertaisesti arvaili vastaukset ja sai kokeesta noin 50 % pisteitä
- Toisaalta oppilas, joka oli painanut mieleen jokaisen luokassa opetetun kysymyksen, pystyi vastaamaan lähes jokaiseen kysymykseen muistinvaraisesti ja sai näin ollen luokkakokeesta 98 %:n pistemäärän
- Opiskelijan C osalta, hän itse asiassa ratkaisi kaikki kysymykset käyttämällä luokassa oppimaansa ongelmanratkaisutapaa ja sai 92 %:n pistemäärän
Voidaan selvästi päätellä, että oppilas, joka vain muistaa kaiken ulkoa, saa paremmat pisteet ilman suurempia vaikeuksia.
Nyt tässä on käänne. Katsotaan myös, mitä tapahtuu kuukausikokeen aikana, kun oppilaat joutuvat kohtaamaan uusia tuntemattomia kysymyksiä, joita opettaja ei ole opettanut tunnilla.

- Opiskelija A:n tapauksessa asiat eivät juuri muuttuneet, ja hän vastaa edelleen sattumanvaraisesti kysymyksiin oikein ~50 %:lla kerralla.
- Opiskelija B:n tapauksessa hänen pistemääränsä putosi huomattavasti. Voitko arvata miksi? Tämä johtuu siitä, että hän on aina opetellut tunnilla opetetut ongelmat ulkoa, mutta tämä kuukausikoe sisälsi kysymyksiä, joita hän ei ole koskaan ennen nähnyt. Siksi hänen suorituksensa laski merkittävästi
- Opiskelija C:n kohdalla pisteet pysyivät kutakuinkin ennallaan. Tämä johtuu siitä, että hän keskittyi ongelmanratkaisun oppimiseen ja pystyi siksi soveltamaan oppimiaan käsitteitä tuntemattomien kysymysten ratkaisemiseen
Miten tämä liittyy ali- ja ylisovittamiseen koneoppimisessa?
Voi olla, että ihmettelet, miten tämä esimerkki liittyy ongelmaan, johon törmäsimme päätöksentekopuu-luokittelijan treenaus- ja testipisteiden aikana? Hyvä kysymys!
Käsitellään siis tämän esimerkin yhdistämistä aiemmin esittelemäni päätöspuu-luokittimen tuloksiin.

Ensiksi, luokkatehtävä ja luokkatesti muistuttavat harjoitteludataa ja itse harjoitteludatan yli tehtyjä ennusteita. Toisaalta lukukausikoe edustaa testijoukkoa datastamme, jonka pidämme sivussa ennen mallin kouluttamista (tai näkemätöntä dataa todellisessa koneoppimisprojektissa).
Nyt muistetaan aiemmin mainitsemani päätöspuu-luokittelijamme. Se antoi täydet pisteet harjoitusjoukossa, mutta kamppaili testijoukon kanssa. Verrattaessa tätä äsken käsittelemiimme opiskelijaesimerkkeihin luokittelija muodostaa analogian opiskelija B:n kanssa, joka yritti opetella ulkoa jokaisen harjoitusjoukon kysymyksen.
Samoin päätöksentekopuuluokittimemme pyrkii oppimaan jokaisen pisteen harjoitusdatasta, mutta kärsii radikaalisti, kun se kohtaa uuden datapisteen testijoukossa. Se ei pysty yleistämään sitä hyvin.

Tätä tilannetta, jossa jokin tietty malli suoriutuu liian hyvin harjoitusdatasta, mutta suorituskyky putoaa merkittävästi testijoukossa, kutsutaan ylisovittuvaksi malliksi.
Esimerkiksi ei-parametriset mallit, kuten päätöspuut, KNN ja muut puupohjaiset algoritmit, ovat hyvin alttiita ylisovittumiselle. Nämä mallit voivat oppia hyvin monimutkaisia suhteita, mikä voi johtaa ylisovittamiseen. Alla oleva kaavio tiivistää tämän käsitteen:
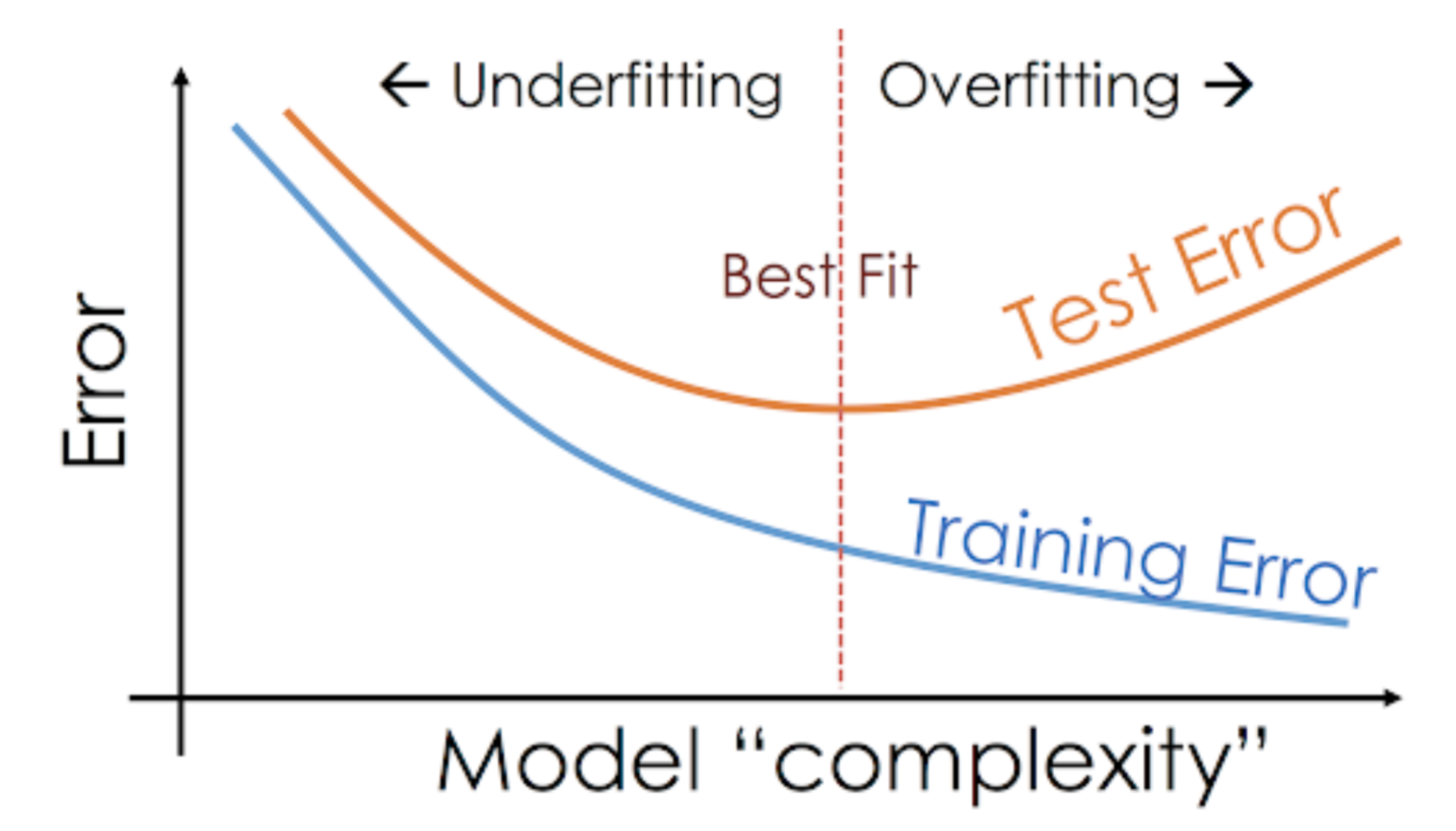
Toisaalta, jos malli suoriutuu huonosti testi- ja harjoitusjoukosta, kutsumme sitä alisovittuvaksi malliksi. Esimerkki tällaisesta tilanteesta olisi lineaarisen regressiomallin rakentaminen epälineaarisen datan yli.

