
De uitdaging van underfitting en overfitting bij machine learning
U zult onvermijdelijk met deze vraag te maken krijgen tijdens een sollicitatiegesprek met een data scientist:
Kunt u uitleggen wat underfitting en overfitting is in de context van machine learning? Beschrijf het op een manier die zelfs een niet-technisch persoon zal begrijpen.
Jouw vermogen om dit op een niet-technische en gemakkelijk te begrijpen manier uit te leggen, zou wel eens de doorslag kunnen geven voor jouw geschiktheid voor de functie van datawetenschapper.
Zelfs als we aan een machine learning-project werken, worden we vaak geconfronteerd met situaties waarin we onverwachte verschillen in prestaties of foutenpercentages tegenkomen tussen de trainingsset en de testset (zoals hieronder afgebeeld). Hoe kan een model zo goed presteren op de trainingsset en net zo slecht op de testset?

Dit gebeurt heel vaak wanneer ik werk met voorspellende modellen op basis van bomen. Door de manier waarop de algoritmen werken, kun je je voorstellen hoe lastig het is om niet in de overfitting-val te trappen!
Meer nog, het kan behoorlijk ontmoedigend zijn als we niet in staat zijn om de onderliggende reden te vinden waarom ons voorspellende model dit afwijkende gedrag vertoont.
Hier volgt mijn persoonlijke ervaring – vraag een doorgewinterde datawetenschapper hierover, en ze beginnen meestal te praten over een reeks fancy termen als Overfitting, Underfitting, Bias, en Variance. Maar weinig mensen hebben het over de intuïtie achter deze machine learning concepten. Laten we dat eens rechtzetten.
Laten we een voorbeeld nemen om Underfitting vs. Overfitting te begrijpen
Ik wil deze concepten uitleggen aan de hand van een voorbeeld uit de echte wereld. Veel mensen hebben het over de theoretische invalshoek, maar volgens mij is dat niet genoeg – we moeten visualiseren hoe underfitting en overfitting feitelijk werken.
Dus, laten we hiervoor teruggaan naar onze studententijd.

Bedenk een wiskundeles die bestaat uit 3 studenten en een professor.
Nu, in elke klas kunnen we de studenten grofweg in 3 categorieën verdelen. We zullen ze een voor een bespreken.

Laten we zeggen dat leerling A lijkt op een leerling die niet van wiskunde houdt. Ze is niet geïnteresseerd in wat er in de klas wordt geleerd en besteedt daarom niet veel aandacht aan de professor en de inhoud die hij onderwijst.

Laten we eens kijken naar student B. Hij is de meest competitieve student die zich concentreert op het uit het hoofd leren van elke vraag die in de klas wordt geleerd in plaats van zich te concentreren op de belangrijkste concepten. In feite is hij niet geïnteresseerd in het leren van de probleemoplossende aanpak.

Ten slotte hebben we de ideale student C. Zij is puur geïnteresseerd in het leren van de belangrijkste concepten en de probleemoplossende aanpak in de wiskundeles in plaats van alleen het uit het hoofd leren van de gepresenteerde oplossingen.

We weten allemaal uit ervaring wat er in een klaslokaal gebeurt. De professor geeft eerst college en leert de leerlingen over de problemen en hoe ze die moeten oplossen. Aan het eind van de dag doet de professor gewoon een quiz, gebaseerd op wat hij in de les heeft geleerd.
Het obstakel komt in de semester3-toetsen die de school voorschrijft. Dit is waar nieuwe vragen (ongeziene gegevens) naar boven komen. De studenten hebben deze vragen nog niet eerder gezien en zeker niet in de klas opgelost. Klinkt dat bekend?
Dus, laten we eens bespreken wat er gebeurt als de leraar aan het eind van de dag een klassikale toets afneemt:

- Student A, die was afgeleid in zijn eigen wereld, raadde gewoon de antwoorden en haalde ongeveer 50% punten voor de test
- Aan de andere kant was de student die elke vraag die in de klas werd geleerd uit het hoofd leerde, in staat om bijna elke vraag uit het hoofd te beantwoorden en haalde daarom 98% punten voor de klassikale test
- Voor student C, loste zij daadwerkelijk alle vragen op met de probleemoplossende aanpak die zij in de klas had geleerd en scoorde 92%
We kunnen hieruit duidelijk afleiden dat de leerling die gewoon alles uit het hoofd leert, zonder veel moeite beter scoort.
Nou hier is de draai. Laten we ook eens kijken naar wat er gebeurt tijdens de maandelijkse test, wanneer studenten te maken krijgen met nieuwe onbekende vragen die niet in de les door de leraar zijn geleerd.

- In het geval van student A veranderde er niet veel en hij beantwoordt nog steeds willekeurig vragen ~50% van de tijd correct.
- In het geval van student B is zijn score aanzienlijk gedaald. Kun je raden waarom? Dit komt omdat hij altijd de problemen die in de klas werden geleerd uit het hoofd leerde, maar deze maandelijkse test bevatte vragen die hij nog nooit eerder heeft gezien. Daarom zijn zijn prestaties aanzienlijk gedaald
- In het geval van student C is de score min of meer gelijk gebleven. Dit komt omdat zij zich concentreerde op het leren van de probleemoplossende aanpak en daardoor in staat was de geleerde concepten toe te passen om de onbekende vragen op te lossen
Hoe verhoudt zich dit tot Underfitting en Overfitting in Machine Learning?
U vraagt zich misschien af hoe dit voorbeeld zich verhoudt tot het probleem dat we tegenkwamen bij de train- en testscores van de beslisboomclassificator? Goede vraag! 
Dus, laten we dit voorbeeld eens verbinden met de resultaten van de beslissingsboom-indeler die ik u eerder heb laten zien.

In de eerste plaats lijken de klassikale test en de klassikale test op respectievelijk de trainingsgegevens en de voorspelling over de trainingsgegevens zelf. Anderzijds vertegenwoordigt de semestertest de testreeks van onze gegevens die we apart houden voordat we ons model trainen (of ongeziene gegevens in een echt machine-learningproject).
Nu, herinner u onze beslissingsboomclassificator die ik eerder noemde. Deze gaf een perfecte score voor de trainingsset, maar had het moeilijk met de testset. Als we dat vergelijken met de voorbeelden van studenten die we zojuist hebben besproken, komt de classificator overeen met student B, die elke vraag in de trainingsset uit zijn hoofd probeerde te leren.
Ook onze beslissingsboomclassificator probeert elk punt van de trainingsgegevens te leren, maar krijgt het zwaar te verduren wanneer hij een nieuw gegevenspunt in de testset tegenkomt. Het is niet in staat om goed te generaliseren.

Deze situatie waarin een bepaald model te goed presteert op de trainingsgegevens, maar de prestaties aanzienlijk afnemen op de testset, wordt een overfitting-model genoemd.
Bij niet-parametrische modellen, zoals beslisbomen, KNN en andere op bomen gebaseerde algoritmen, is overfitting zeer waarschijnlijk. Deze modellen kunnen zeer complexe relaties aanleren, wat tot overfitting kan leiden. De onderstaande grafiek vat dit concept samen:
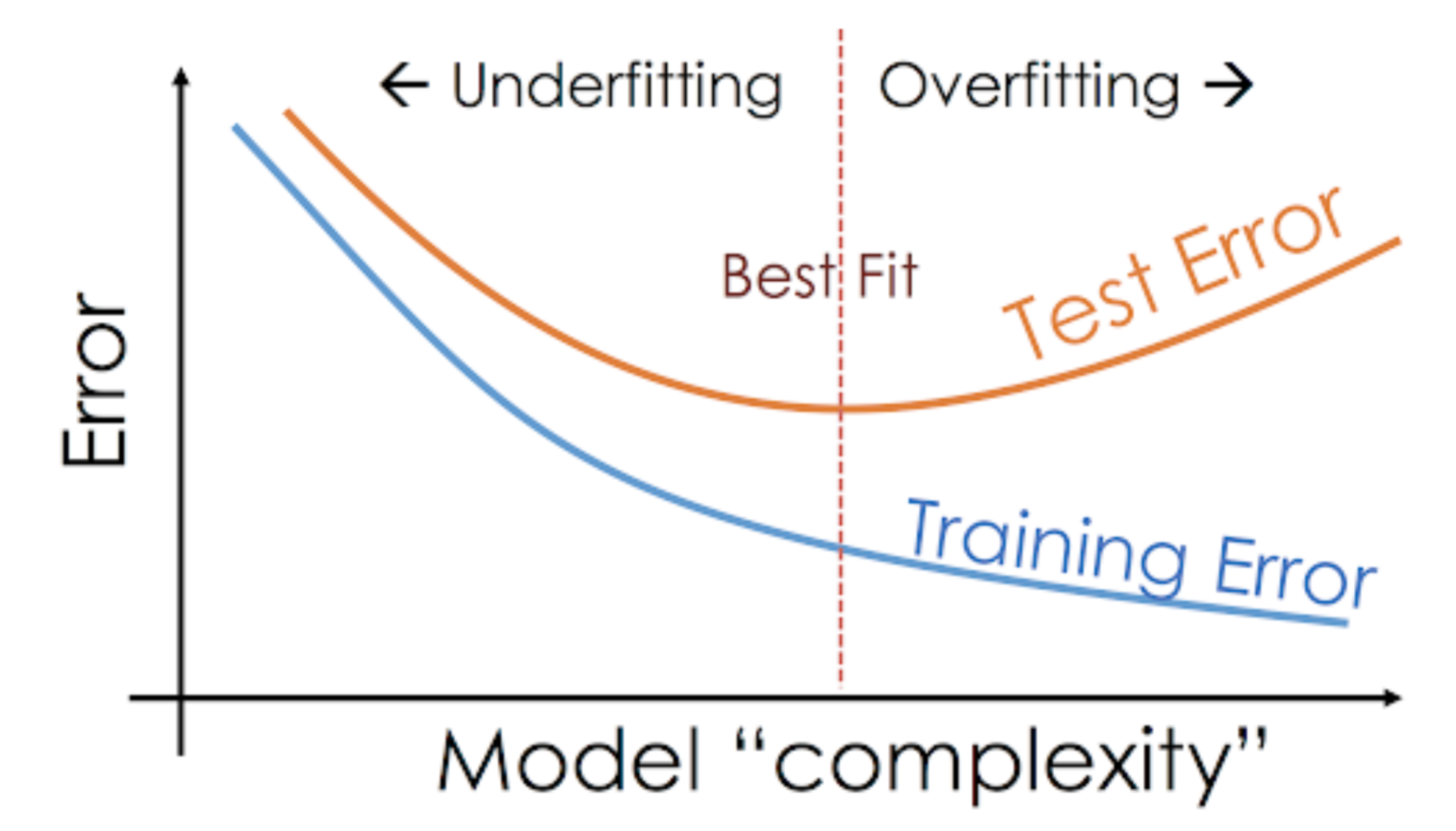
Aan de andere kant, als het model slecht presteert over de test- en de treinset, dan noemen we dat een underfitting-model. Een voorbeeld van een dergelijke situatie is het bouwen van een lineair regressiemodel over niet-lineaire gegevens.

