
Az underfitting és overfitting kihívása a gépi tanulásban
Ezzel a kérdéssel elkerülhetetlenül találkozol egy adattudós interjún:
Meg tudnád magyarázni, mi az underfitting és overfitting a gépi tanulással összefüggésben? Írja le úgy, hogy azt még egy nem műszaki szakember is felfogja!
Az, hogy ezt nem műszaki és könnyen érthető módon tudja elmagyarázni, könnyen eldöntheti, hogy alkalmas-e az adattudományi pozícióra!
A gépi tanulási projekteken dolgozva is gyakran találkozunk olyan helyzetekkel, amikor váratlan teljesítmény- vagy hibaaránykülönbségekkel találkozunk a gyakorlóhalmaz és a teszthalmaz között (mint az alábbiakban látható). Hogyan lehetséges, hogy egy modell ilyen jól teljesít a gyakorlóhalmazon, és ugyanolyan rosszul a teszthalmazon?

Ez nagyon gyakran előfordul, amikor faalapú előrejelző modellekkel dolgozom. Az algoritmusok működésének módja miatt el tudja képzelni, milyen trükkös dolog elkerülni, hogy a túlillesztés csapdájába essünk!
Még inkább ijesztő lehet, ha nem tudjuk megtalálni a mögöttes okot, amiért a prediktív modellünk ilyen rendellenes viselkedést mutat.
Itt a személyes tapasztalatom – kérdezzen erről bármelyik tapasztalt adattudóst, ők általában olyan díszes kifejezésekről kezdenek beszélni, mint a túlillesztés, alulillesztés, torzítás és szórás. De kevesen beszélnek az intuícióról, ami ezek mögött a gépi tanulási fogalmak mögött van. Javítsuk ki ezt, rendben?
Vegyünk egy példát az Underfitting vs. Overfitting megértéséhez
Egy valós példán keresztül szeretném elmagyarázni ezeket a fogalmakat. Sokan beszélnek az elméleti szemszögről, de úgy érzem, hogy ez nem elég – szemléltetnünk kell, hogyan működik valójában az alul- és túlillesztés.
Szóval, térjünk vissza az egyetemi időkbe ehhez.

Gondoljunk egy 3 diákból és egy tanárból álló matematikaórára.
Most, bármelyik osztályteremben nagyjából 3 kategóriára oszthatjuk a diákokat. Egyenként beszélünk róluk.

Tegyük fel, hogy A diák hasonlít egy olyan diákra, aki nem szereti a matematikát. Nem érdekli, hogy mit tanítanak az órán, ezért nem is figyel a professzorra és az általa tanított tartalomra.

Lássuk B diákot. Ő a legversengőbb diák, aki arra összpontosít, hogy minden egyes kérdést bemagoljon, amit az órán tanítanak, ahelyett, hogy a kulcsfogalmakra koncentrálna. Alapvetően nem érdekli a problémamegoldó megközelítés megtanulása.

Végül itt van az ideális diák C. Őt tisztán a kulcsfogalmak és a problémamegoldó megközelítés megtanulása érdekli a matematikaórán, ahelyett, hogy csak bemagolná a bemutatott megoldásokat.

Mindannyian tudjuk tapasztalatból, mi történik az osztályteremben. A professzor először előadásokat tart, és megtanítja a diákokat a problémákra és azok megoldására. A nap végén a professzor egyszerűen felvesz egy tesztet az órán tanultak alapján.
Az akadály a félévi3 tesztekben van, amelyeket az iskola ír ki. Itt ugyanis új kérdések (nem látott adatok) merülnek fel. A diákok még nem látták ezeket a kérdéseket, és biztosan nem oldották meg őket az órán. Ismerősen hangzik?
Azt beszéljük meg tehát, hogy mi történik, amikor a tanár a nap végén osztálytermi tesztet ír:

- A tanuló A, aki el volt zavarodva a saját világában, egyszerűen kitalálta a válaszokat, és körülbelül 50%-os pontszámot kapott a tesztben
- A másik oldalon az a tanuló, aki minden egyes, az osztályteremben tanított kérdést megjegyzett, szinte minden kérdésre emlékezetből tudott válaszolni, és ezért 98%-os pontszámot kapott az osztálytesztben
- A tanuló C esetében, ő valóban minden kérdést megoldott az osztályteremben tanult problémamegoldó módszerrel, és 92%-os eredményt ért el
Egyértelműen arra következtethetünk, hogy az a tanuló, aki egyszerűen mindent megjegyez, nagyobb nehézség nélkül jobb eredményt ér el.
És most jön a csavar. Nézzük meg azt is, mi történik a havi teszt során, amikor a diákoknak új, ismeretlen kérdésekkel kell szembenézniük, amelyeket a tanár nem tanított meg az órán.

- A diák A esetében a dolgok nem sokat változtak, és még mindig véletlenszerűen válaszol helyesen a kérdésekre ~50%-ban.
- A diák B esetében a pontszáma jelentősen csökkent. Ki tudja találni, hogy miért? Ez azért van, mert mindig megjegyezte az órán tanult feladatokat, de ez a havi teszt olyan kérdéseket tartalmazott, amelyeket még soha nem látott. Ezért a teljesítménye jelentősen csökkent
- A C tanuló esetében a pontszáma többé-kevésbé változatlan maradt. Ennek az az oka, hogy a problémamegoldó megközelítés tanulására összpontosított, és ezért képes volt alkalmazni a tanult fogalmakat az ismeretlen kérdések megoldására
Hogyan kapcsolódik ez az alul- és túlillesztéshez a gépi tanulásban?
Elképzelhető, hogy ez a példa hogyan kapcsolódik ahhoz a problémához, amellyel a döntési fa osztályozó edzés- és tesztpontszámai során találkoztunk? Jó kérdés!
Foglalkozzunk tehát azzal, hogy ezt a példát összekapcsoljuk a döntési fa osztályozó eredményével, amelyet korábban bemutattam.

Először is, az osztályteszt és az osztályteszt hasonlít a képzési adatokra, illetve magára a képzési adatok feletti előrejelzésre. Másrészt a félévi teszt a tesztkészletet képviseli az adatainkból, amelyeket félreteszünk, mielőtt betanítjuk a modellünket (vagy nem látott adatokat egy valós gépi tanulási projektben).
Most, emlékezzünk vissza a korábban említett döntési fa osztályozónkra. A képzési halmazon tökéletes eredményt adott, de a teszthalmazon küszködött. Ha ezt összehasonlítjuk az imént tárgyalt tanulói példákkal, az osztályozó analógiát állít fel B tanulóval, aki megpróbált minden egyes kérdést megjegyezni a gyakorlóhalmazban.
Hasonlóképpen a döntési fa osztályozónk is megpróbál minden egyes pontot megtanulni a gyakorlóadatokból, de radikálisan szenved, amikor a teszthalmazban új adatponttal találkozik. Nem képes jól általánosítani.

Ezt a helyzetet, amikor egy adott modell túl jól teljesít a képzési adatokon, de a tesztkészleten jelentősen csökken a teljesítménye, túlilleszkedő modellnek nevezzük.
A nem parametrikus modellek, például a döntési fák, a KNN és más faalapú algoritmusok nagyon hajlamosak a túlilleszkedésre. Ezek a modellek nagyon összetett összefüggéseket tanulhatnak, ami túlillesztést eredményezhet. Az alábbi grafikon összefoglalja ezt a fogalmat:
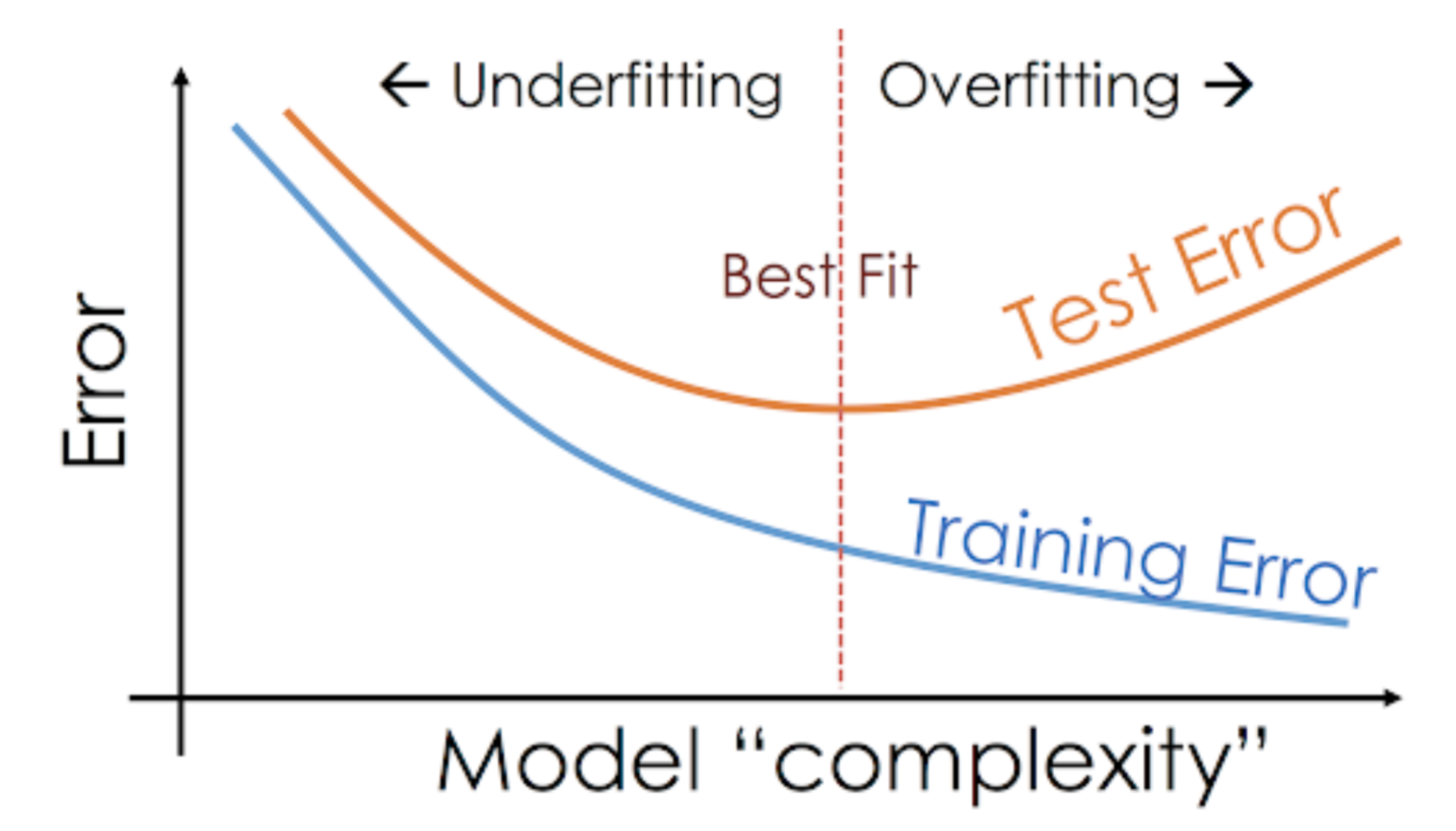
Másrészt, ha a modell rosszul teljesít a teszt- és a tanulóhalmazon, akkor azt alulilleszkedő modellnek nevezzük. Egy példa erre a helyzetre egy lineáris regressziós modell építése nem lineáris adatok felett.

