
Udfordringen ved underfitting og overfitting i maskinlæring
Du vil uundgåeligt blive stillet dette spørgsmål i et interview med en datamatiker:
Kan du forklare, hvad underfitting og overfitting er i forbindelse med maskinlæring? Beskriv det på en måde, som selv en ikke-teknisk person vil forstå.
Din evne til at forklare dette på en ikke-teknisk og letforståelig måde kan meget vel være afgørende for, om du passer til rollen som datavidenskabsmand!
Selv når vi arbejder på et maskinlæringsprojekt, står vi ofte over for situationer, hvor vi støder på uventede forskelle i ydeevne eller fejlprocent mellem træningsmængden og testmængden (som vist nedenfor). Hvordan kan en model præstere så godt på træningsmængden og lige så dårligt på testmængden?

Dette sker meget ofte, når jeg arbejder med træbaserede forudsigelsesmodeller. På grund af den måde, algoritmerne fungerer på, kan du forestille dig, hvor svært det er at undgå at falde i overfitting-fælden!
Det kan desuden være ret skræmmende, når vi ikke er i stand til at finde den underliggende årsag til, at vores prædiktive model udviser denne unormale adfærd.
Her er min personlige erfaring – spørg en erfaren datalog om dette, og de begynder typisk at tale om en række smarte termer som Overfitting, Underfitting, Bias og Varians. Men der er meget lidt nogen der taler om intuitionen bag disse maskinlæringsbegreber. Lad os rette op på det, skal vi?
Lad os tage et eksempel for at forstå Underfitting vs. Overfitting
Jeg vil gerne forklare disse begreber ved hjælp af et eksempel fra den virkelige verden. Mange folk taler om den teoretiske vinkel, men jeg føler, at det ikke er nok – vi skal visualisere, hvordan underfitting og overfitting rent faktisk fungerer.
Så lad os gå tilbage til vores college-dage til dette.

Tænk på en matematikklasse bestående af 3 studerende og en professor.
Nu kan vi i ethvert klasseværelse groft sagt opdele de studerende i 3 kategorier. Vi vil tale om dem en for en.

Lad os sige, at elev A ligner en elev, der ikke kan lide matematik. Hun er ikke interesseret i det, der bliver undervist i klassen, og derfor er hun ikke særlig opmærksom på professoren og det indhold, han underviser i.

Lad os overveje elev B. Han er den mest konkurrencemindede elev, der fokuserer på at lære hvert eneste spørgsmål, der bliver undervist i klassen, udenad i stedet for at fokusere på de centrale begreber. Dybest set er han ikke interesseret i at lære den problemløsende tilgang.

Sidst har vi den ideelle elev C. Hun er udelukkende interesseret i at lære nøglebegreberne og den problemløsende tilgang i matematiktimerne frem for blot at lære de præsenterede løsninger udenad.

Vi ved alle af erfaring, hvad der sker i et klasseværelse. Professoren holder først forelæsninger og lærer eleverne om problemerne, og hvordan de skal løses. Til sidst tager professoren blot en quiz baseret på det, han har undervist i klassen.
Hindringen kommer i de semester3 prøver, som skolen lægger ud. Det er her, at nye spørgsmål (usete data) kommer frem. De studerende har ikke set disse spørgsmål før, og de har bestemt ikke løst dem i undervisningen. Lyder det bekendt?
Så lad os diskutere, hvad der sker, når læreren tager en klasseprøve i slutningen af dagen:

- Eelev A, der var distraheret i sin egen verden, gættede blot svarene og fik ca. 50 % point i prøven
- På den anden side var den elev, der lærte hvert eneste spørgsmål, der blev undervist i klasseværelset, i stand til at besvare næsten alle spørgsmål udenad og fik derfor 98 % point i klassetesten
- For elev C, løste hun faktisk alle spørgsmålene ved hjælp af den problemløsningstilgang, hun lærte i klasseværelset, og scorede 92%
Vi kan klart udlede, at den elev, der blot lærer alt udenad, scorer bedre uden større problemer.
Nu er det her, der er det sjove. Lad os også se på, hvad der sker under den månedlige prøve, hvor eleverne skal stå over for nye ukendte spørgsmål, som læreren ikke har lært i klassen.

- For elev A ændrede tingene sig ikke meget, og han svarer stadig tilfældigt korrekt på spørgsmålene ~50 % af gangene.
- For elev B faldt hans score betydeligt. Kan du gætte hvorfor? Det skyldes, at han altid har lært de problemer udenad, der blev undervist i klassen, men denne månedlige prøve indeholdt spørgsmål, som han aldrig har set før. Derfor faldt hans præstation betydeligt
- For elev C forblev resultatet mere eller mindre det samme. Dette skyldes, at hun fokuserede på at lære problemløsningstilgangen og derfor var i stand til at anvende de begreber, hun lærte, til at løse de ukendte spørgsmål
Hvordan hænger dette sammen med Underfitting og Overfitting i maskinlæring?
Du undrer dig måske over, hvordan dette eksempel hænger sammen med det problem, som vi stødte på under train- og testscoren for beslutningstræets klassifikator? Godt spørgsmål!
Så lad os arbejde på at forbinde dette eksempel med resultaterne af beslutningstræklassificatoren, som jeg viste dig tidligere.

Først ligner klassetræningen og klassetesten henholdsvis træningsdataene og forudsigelsen over selve træningsdataene. På den anden side repræsenterer semestertesten det testsæt fra vores data, som vi holder til side, før vi træner vores model (eller usete data i et virkeligt maskinlæringsprojekt).
Nu skal du huske vores beslutningstræklassifikator, som jeg nævnte tidligere. Den gav en perfekt score over træningsmængden, men havde det svært med testmængden. Sammenligner man det med de eleveksempler, vi lige har diskuteret, etablerer klassifikatoren en analogi med elev B, der forsøgte at lære hvert eneste spørgsmål i træningssættet udenad.
På samme måde forsøger vores beslutningstræklassifikator at lære hvert eneste punkt fra træningsdataene, men lider radikalt, når den støder på et nyt datapunkt i testsættet. Den er ikke i stand til at generalisere det godt.

Denne situation, hvor en given model klarer sig for godt på træningsdataene, men hvor præstationen falder betydeligt i forhold til testsættet, kaldes en overfitting-model.
For eksempel er ikke-parametriske modeller som beslutningstræer, KNN og andre træbaserede algoritmer meget tilbøjelige til at overfitte. Disse modeller kan lære meget komplekse relationer, hvilket kan resultere i overfitting. Nedenstående graf opsummerer dette begreb:
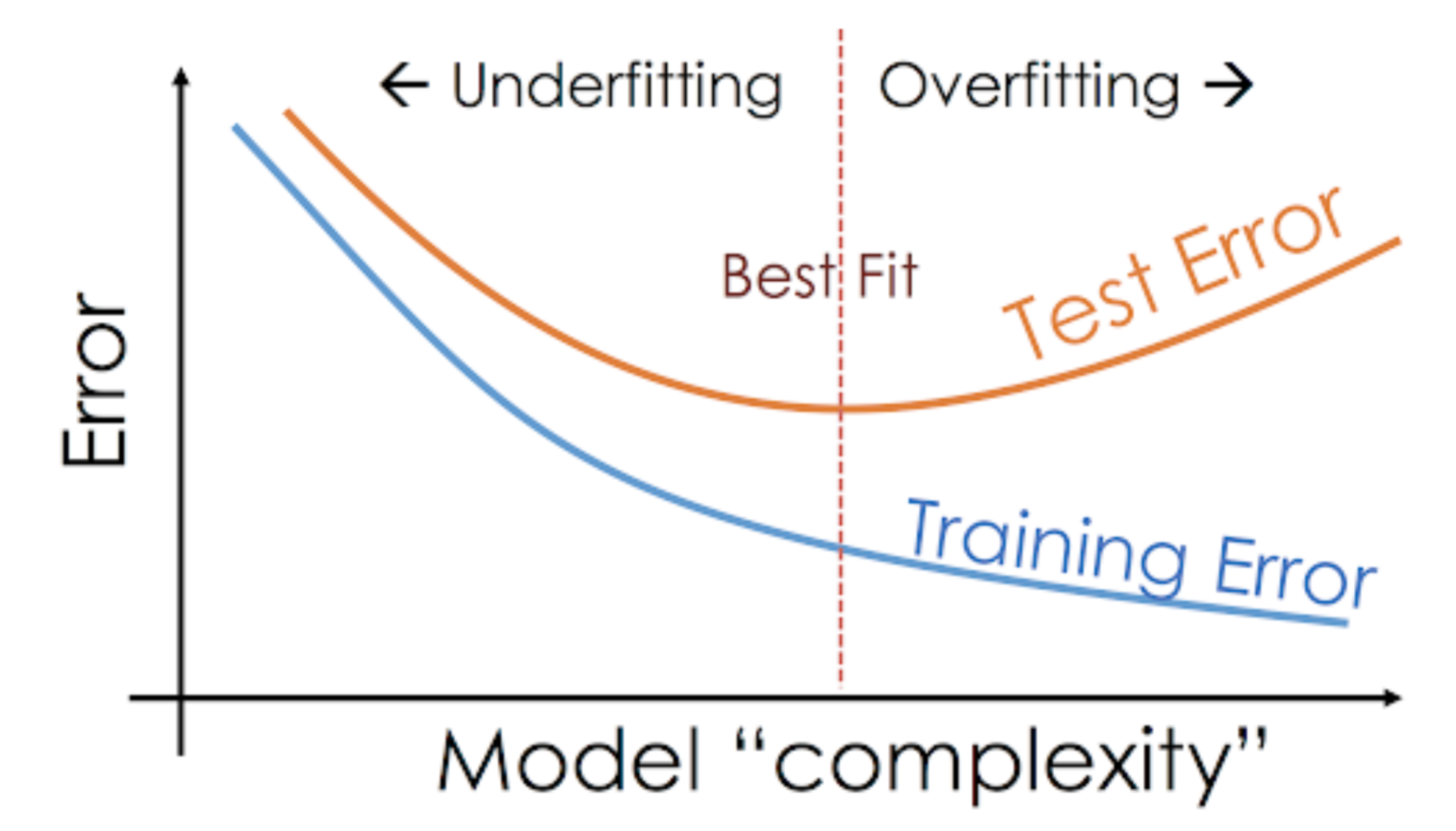
På den anden side, hvis modellen klarer sig dårligt over test- og træningssættet, kalder vi det en underfitting-model. Et eksempel på denne situation ville være at opbygge en lineær regressionsmodel over ikke-lineære data.

