
The Challenge of Underfitting and Overfitting in Machine Learning
Při pohovoru s datovým vědcem se nevyhnutelně setkáte s touto otázkou:
Můžete vysvětlit, co je to underfitting a overfitting v kontextu strojového učení? Popište to tak, aby to pochopil i netechnický člověk.
Vaše schopnost vysvětlit to netechnicky a srozumitelně může rozhodnout o tom, zda se hodíte na pozici datového vědce!
I když pracujeme na projektu strojového učení, často se setkáváme se situacemi, kdy narážíme na neočekávané rozdíly ve výkonu nebo chybovosti mezi trénovací a testovací množinou (jak je uvedeno níže). Jak je možné, že model má tak dobrý výkon na trénovací množině a stejně špatný na testovací množině?“

To se stává velmi často, kdykoli pracuji s predikčními modely založenými na stromech. Vzhledem ke způsobu, jakým tyto algoritmy fungují, si dokážete představit, jak složité je vyhnout se tomu, abychom spadli do pasti overfittingu!
Mimo to může být docela skličující, když nejsme schopni najít základní důvod, proč náš prediktivní model vykazuje toto anomální chování.
Tady je moje osobní zkušenost – zeptejte se na to jakéhokoli zkušeného datového vědce a obvykle začne mluvit o nějaké řadě módních termínů jako Overfitting, Underfitting, Bias a Variance. Ale málokdo mluví o intuici, která za těmito pojmy strojového učení stojí. Pojďme to napravit, ano?“
Podívejme se na příklad, abychom pochopili Underfitting vs. Overfitting
Chci tyto pojmy vysvětlit na příkladu z reálného světa. Mnoho lidí mluví o teoretickém úhlu pohledu, ale mám pocit, že to nestačí – potřebujeme si představit, jak underfitting a overfitting skutečně fungují.
Vraťme se tedy kvůli tomu do našich vysokoškolských časů.

Představme si třídu matematiky, která se skládá ze 3 studentů a profesora.
V každé třídě můžeme studenty rámcově rozdělit do 3 kategorií. Budeme o nich mluvit postupně.

Řekněme, že student A se podobá studentovi, který nemá rád matematiku. Nezajímá se o to, co se v hodině učí, a proto nevěnuje profesorovi a obsahu, který učí, velkou pozornost.

Uvažujme o studentovi B. Je to nejsoutěživější student, který se soustředí na zapamatování každé otázky, která se v hodině učí, místo aby se soustředil na klíčové pojmy. V podstatě nemá zájem o učení se přístupu k řešení problémů.

Nakonec máme ideálního studenta C. Má čistě zájem o učení se klíčovým pojmům a přístupu k řešení problémů v hodinách matematiky spíše než o pouhé memorování předložených řešení.

Všichni ze zkušenosti víme, co se ve třídě děje. Profesor nejprve přednáší a učí studenty problémům a jejich řešení. Na konci dne profesor prostě udělá test na základě toho, co učil v hodině.
Překážka nastává v pololetních3 testech, které škola stanoví. Zde se objevují nové otázky (neviděné údaje). Studenti tyto otázky ještě neviděli a rozhodně je neřešili ve třídě. Zní vám to povědomě?
Probereme tedy, co se stane, když učitel na konci dne vypracuje třídní test:

- Žák A, který byl rozptýlen ve svém vlastním světě, odpovědi jednoduše uhodl a v testu získal přibližně 50 % bodů
- Naopak žák, který si zapamatoval každou otázku vyučovanou ve třídě, dokázal téměř na každou otázku odpovědět zpaměti, a proto v třídním testu získal 98 % bodů
- Pro žáka C, skutečně vyřešila všechny otázky pomocí přístupu k řešení problémů, který se naučila ve třídě, a získala 92 % bodů
Můžeme z toho jasně vyvodit, že studentka, která si vše jednoduše zapamatuje, dosahuje lepších výsledků bez větších obtíží.
Nyní přichází zvrat. Podívejme se také na to, co se děje během měsíčního testu, kdy studenti musí čelit novým neznámým otázkám, které učitel v hodinách neučil.

- V případě studenta A se situace příliš nezměnila a stále náhodně odpovídá na otázky správně v ~50 % případů.
- V případě studenta B jeho skóre výrazně pokleslo. Dokážete odhadnout proč? Je to proto, že si vždy zapamatoval úlohy, které se učil v hodině, ale tento měsíční test obsahoval otázky, které nikdy předtím neviděl. Proto jeho výkon výrazně poklesl
- V případě studenta C zůstalo skóre víceméně stejné. Je to proto, že se soustředila na výuku přístupu k řešení problémů, a proto byla schopna použít naučené koncepty k řešení neznámých otázek
Jak to souvisí s nedostatečným a nadměrným přizpůsobením ve strojovém učení
Možná vás zajímá, jak tento příklad souvisí s problémem, se kterým jsme se setkali při trénování a testování výsledků klasifikátoru rozhodovacího stromu? Dobrá otázka!
Pracujme tedy na propojení tohoto příkladu s výsledky klasifikátoru rozhodovacího stromu, které jsem vám ukázal dříve.

Předně, třída práce a třída test připomínají tréninková data, respektive předpověď nad samotnými tréninkovými daty. Na druhou stranu semestrální test představuje testovací množinu z našich dat, kterou si necháváme stranou před trénováním našeho modelu (nebo neviděná data v reálném projektu strojového učení).
Nyní si vzpomeňte na náš klasifikátor rozhodovacího stromu, o kterém jsem se zmínil dříve. V trénovací množině dosáhl perfektního skóre, ale měl potíže s testovací množinou. Porovnáme-li to s příklady studentů, o kterých jsme právě hovořili, vytvoří klasifikátor analogii se studentem B, který se snažil zapamatovat si každou otázku v trénovací množině.
Podobně se náš klasifikátor rozhodovacího stromu snaží naučit každý bod z trénovacích dat, ale radikálně trpí, když narazí na nový bod dat v testovací množině. Není schopen jej dobře zobecnit.

Tuto situaci, kdy nějaký model funguje příliš dobře na trénovacích datech, ale jeho výkonnost výrazně klesá nad testovací množinou, nazýváme overfitting modelu.
Například neparametrické modely, jako jsou rozhodovací stromy, KNN a další algoritmy založené na stromech, jsou velmi náchylné k overfittingu. Tyto modely se mohou naučit velmi složité vztahy, které mohou vést k overfittingu. Níže uvedený graf shrnuje tento koncept:
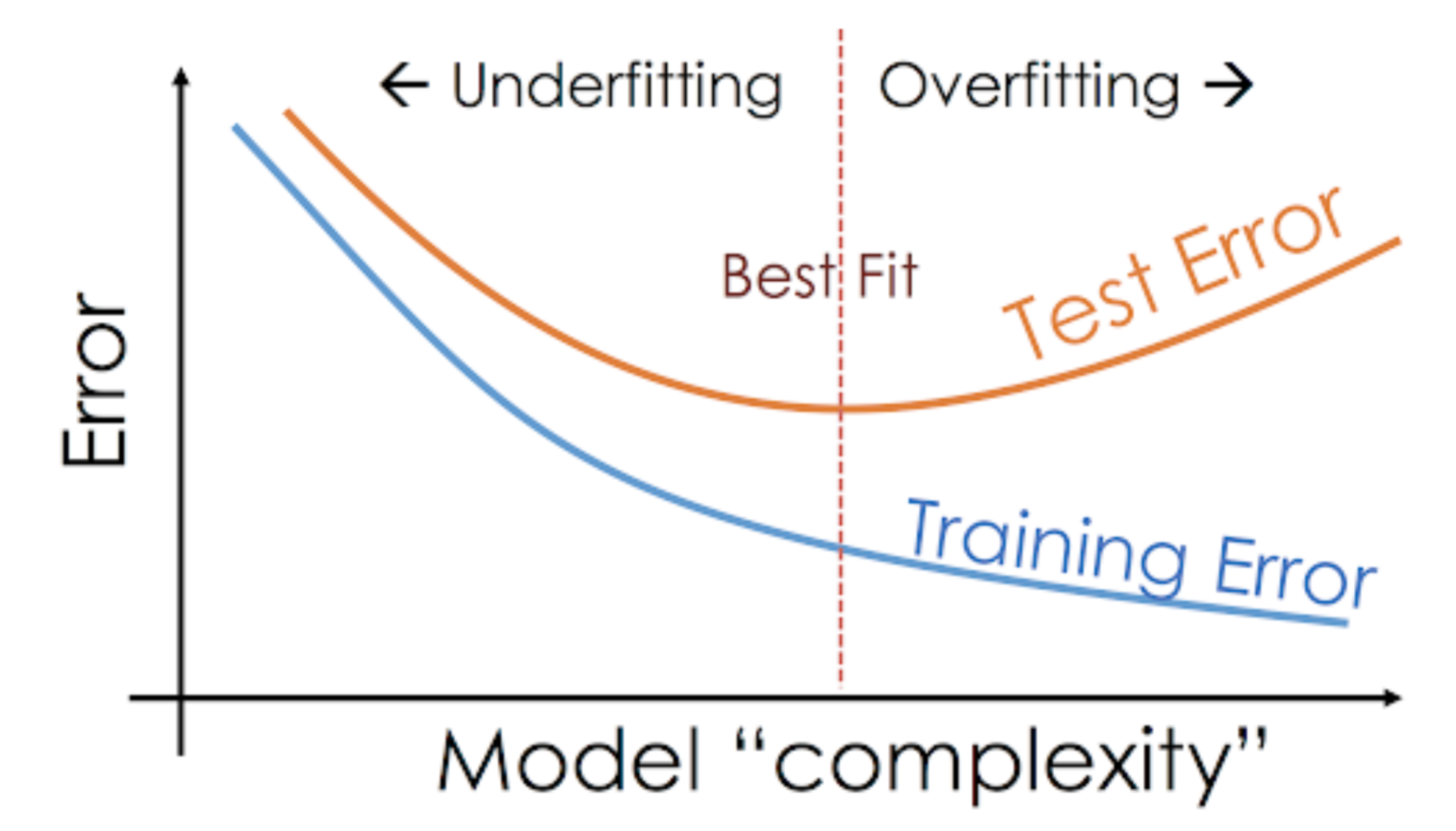
Na druhou stranu, pokud si model vede špatně nad testovací a trénovací množinou, pak tomu říkáme nedostatečně fitující model. Příkladem takové situace může být sestavení lineárního regresního modelu nad nelineárními daty.

.
