Grundfunktioner
I det här avsnittet graferar vi sju grundfunktioner som kommer att användas under hela kursen. Varje funktion grafiseras genom att man plottar punkter. Kom ihåg att f(x)=y och därmed kan f(x) och y användas omväxlande.
Alla funktioner av formen f(x)=c, där c är ett reellt tal, kallas konstanta funktionerAlla funktioner av formen f(x)=c där c är ett reellt tal… Konstanta funktioner är linjära och kan skrivas f(x)=0x+c. I denna form är det tydligt att lutningen är 0 och y-interceptet är (0,c). Om man utvärderar ett valfritt värde för x, till exempel x = 2, blir resultatet c.
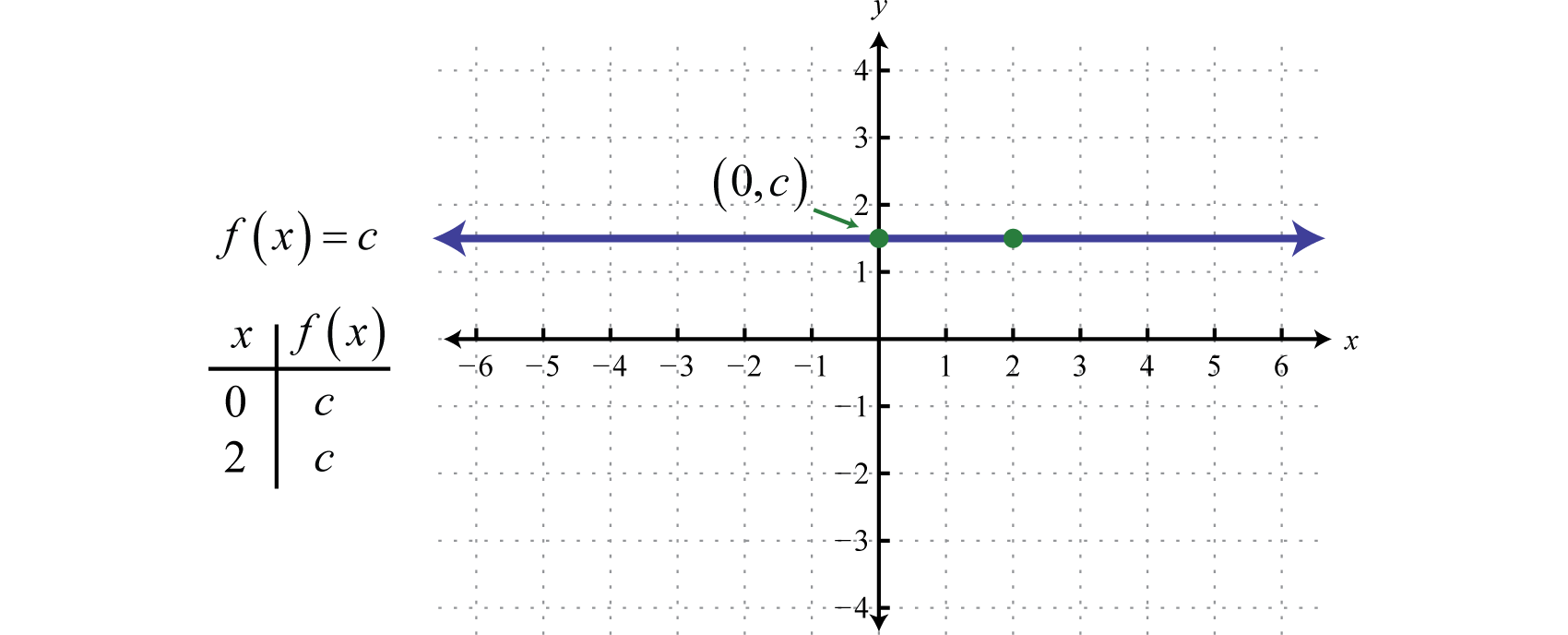
Grafen för en konstant funktion är en horisontell linje. Domänen består av alla reella tal ℝ och området består av det enda värdet {c}.
Vi definierar härnäst identitetsfunktionenDen linjära funktionen som definieras genom f(x)=x. f(x)=x. Att utvärdera ett valfritt värde för x kommer att resultera i samma värde. Till exempel f(0)=0 och f(2)=2. Identitetsfunktionen är linjär, f(x)=1x+0, med lutning m=1 och y-intercept (0, 0).
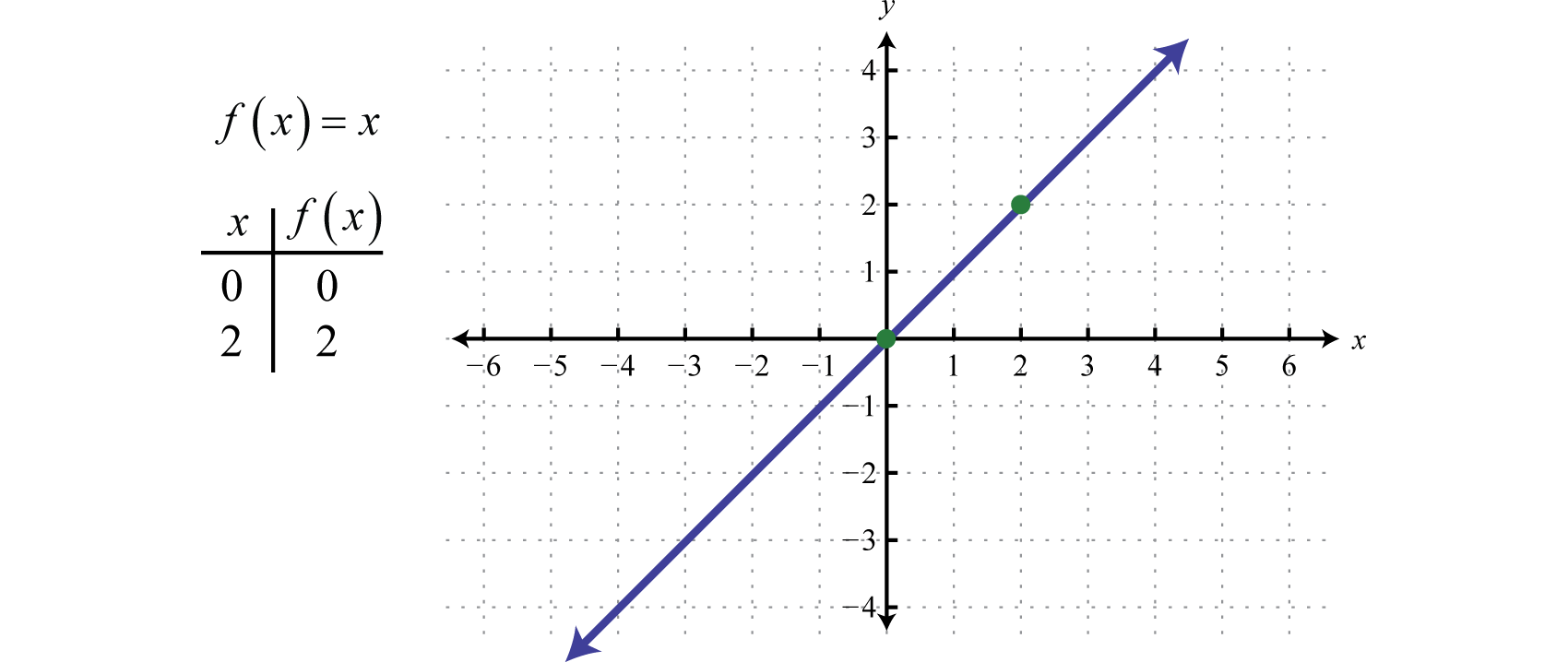
Domänen och intervallet består båda av alla reella tal.
KvadratfunktionenDen kvadratiska funktionen definierad genom f(x)=x2., definierad genom f(x)=x2, är den funktion som erhålls genom att kvadrera värdena i domänen. Till exempel f(2)=(2)2=4 och f(-2)=(-2)2=4. Resultatet av kvadrering av värden som inte är noll i domänen kommer alltid att vara positivt.
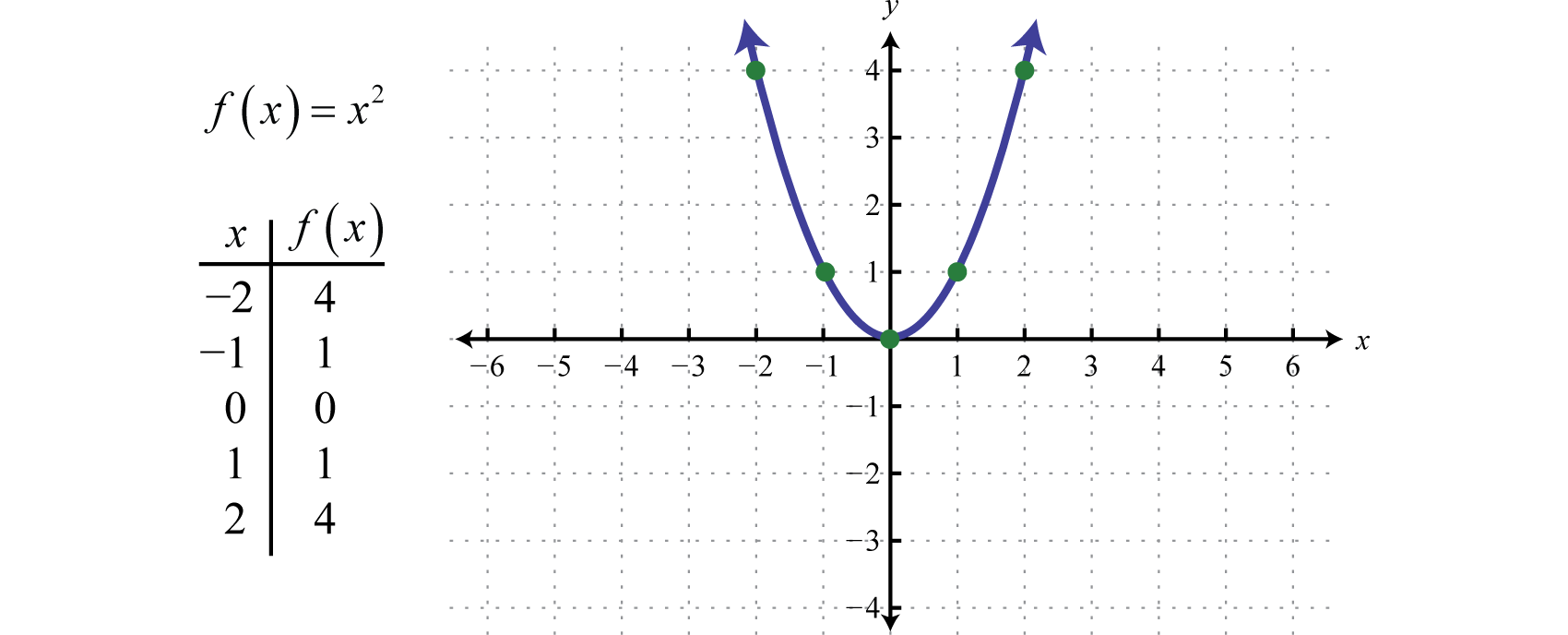
Den resulterande krökta grafen kallas en parabelDen krökta grafen som bildas av kvadreringsfunktionen… Domänen består av alla reella tal ℝ och området består av alla y-värden som är större än eller lika med noll [0,∞).
KubikfunktionenKubikfunktionen som definieras av f(x)=x3., som definieras av f(x)=x3, höjer alla värden i domänen till den tredje potensen. Resultaten kan vara antingen positiva, noll eller negativa. Till exempel: f(1)=(1)3=1, f(0)=(0)3=0 och f(-1)=(-1)3=-1.
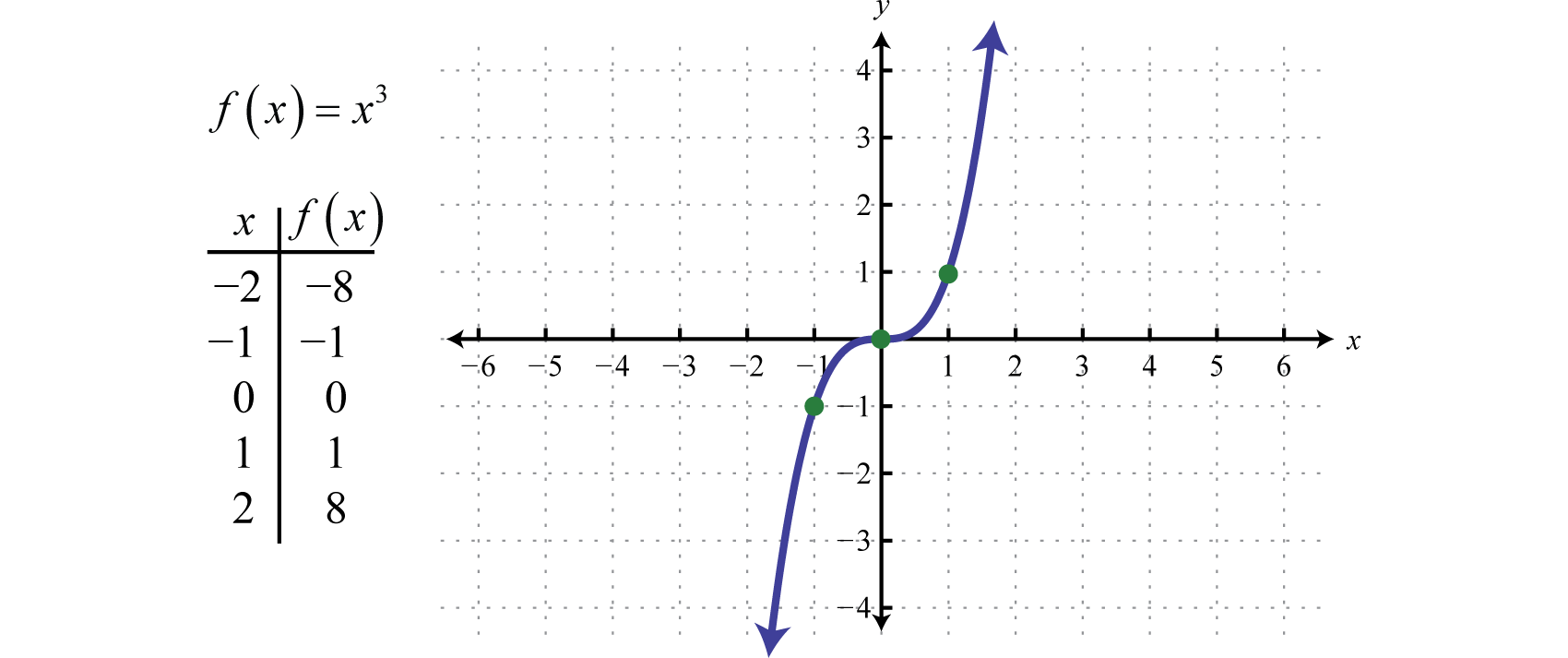
Domänen och intervallet består båda av alla reella tal ℝ.
Bemärk att konstant-, identitets-, kvadrerings- och kubikfunktionerna alla är exempel på grundläggande polynomialfunktioner. De tre följande grundläggande funktionerna är inte polynomier.
AbsolutvärdesfunktionenFunktionen definierad genom f(x)=|x|., definierad genom f(x)=|x|, är en funktion där utfallet representerar avståndet till origo på en tallinje. Resultatet av utvärderingen av absolutvärdesfunktionen för varje icke-nollvärde av x kommer alltid att vara positivt. Till exempel f(-2)=|-2|=2 och f(2)=|2|=2.
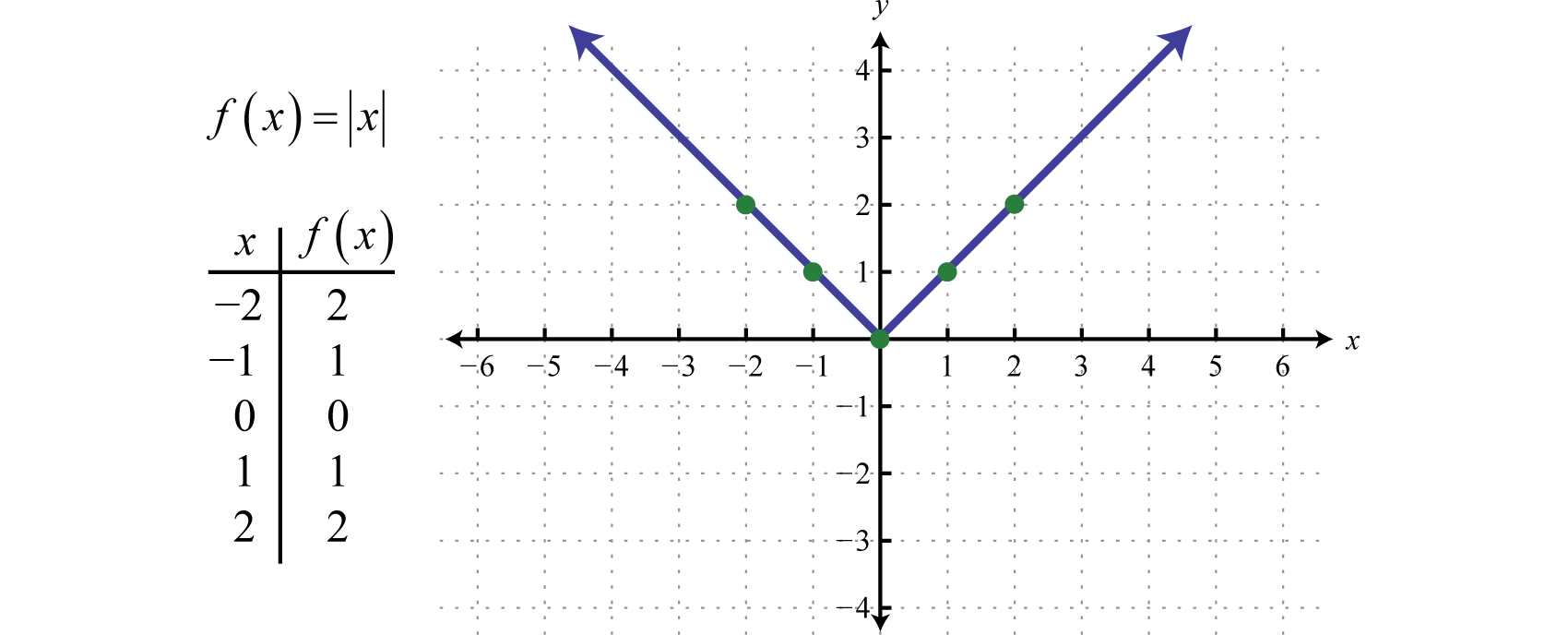
Absolutvärdesfunktionens domän består av alla reella tal ℝ och intervallet består av alla y-värden som är större än eller lika med noll [0,∞).
KvadratrotsfunktionenFunktionen som definieras av f(x)=x., som definieras genom f(x)=x, definieras inte som ett reellt tal om x-värdena är negativa. Därför är det minsta värdet i domänen noll. Exempelvis f(0)=0=0 och f(4)=4=2.
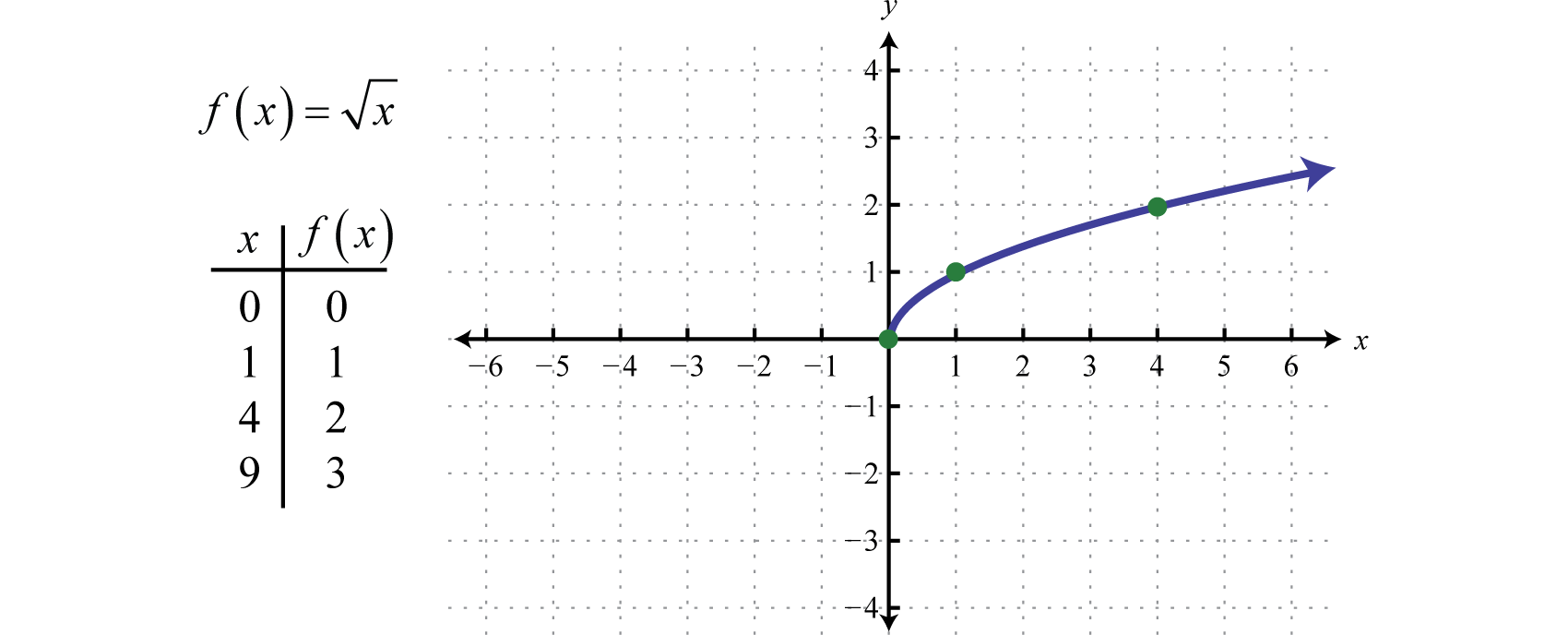
Domänen och området består båda av reella tal som är större än eller lika med noll [0,∞).
Den reciproka funktionenFunktionen definierad genom f(x)=1x., definierad genom f(x)=1x, är en rationell funktion med en begränsning på domänen, nämligen x≠0. Reciproken av ett x-värde som ligger mycket nära noll är mycket stor. Till exempel
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1 000)=1(11 000)=1⋅1,0001=1 000
Med andra ord, när x-värdena närmar sig noll kommer deras reciprok att tendera mot antingen positiv eller negativ oändlighet. Detta beskriver en vertikal asymptotEn vertikal linje som en graf kommer oändligt nära. på y-axeln. När x-värdena är mycket stora blir dessutom resultatet av den reciproka funktionen mycket litet.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11 000=0,001
Med andra ord tenderar de resulterande y-värdena mot noll när x-värdena blir mycket stora. Detta beskriver en horisontell asymptotEn horisontell linje som en graf blir oändligt nära där x-värdena tenderar mot ±∞. vid x-axeln. Efter att ha plottat ett antal punkter kan den reciproka funktionens allmänna form bestämmas.
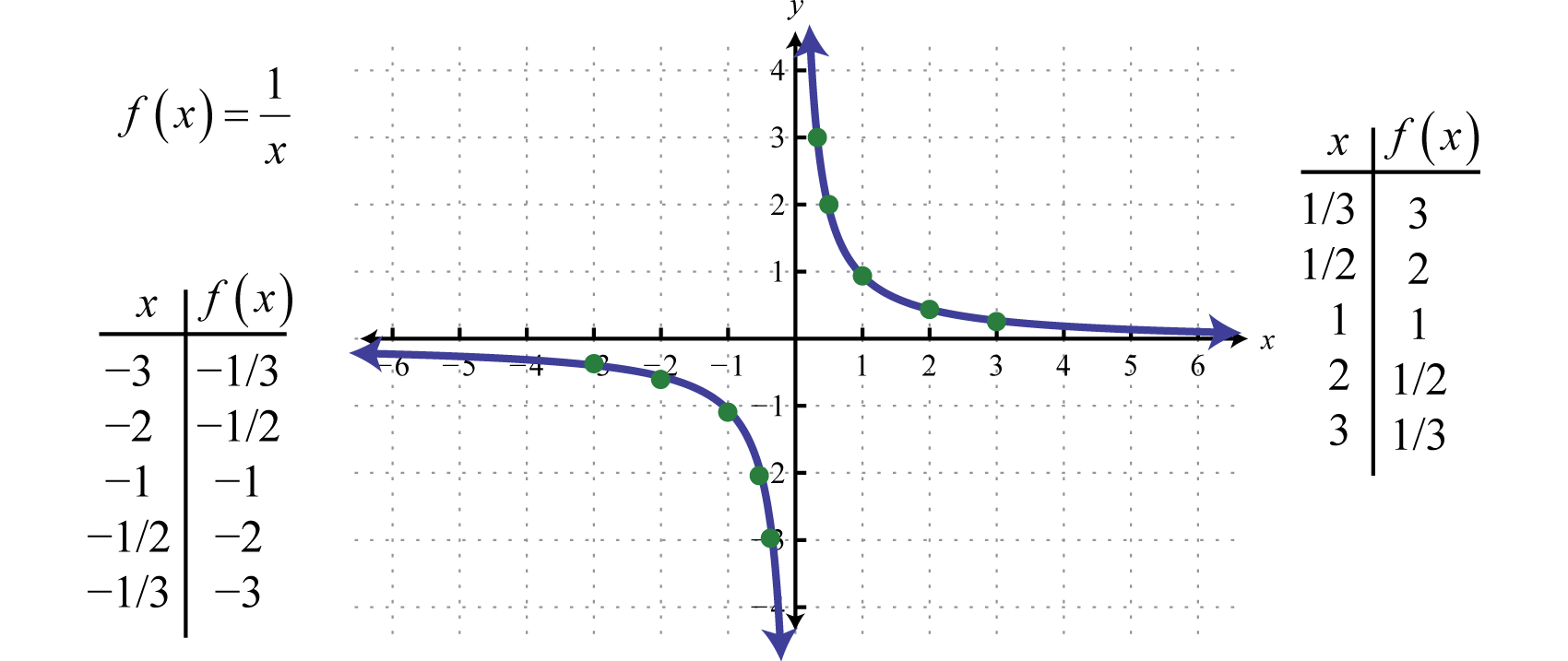
Både den reciproka funktionens domän och område består av alla reella tal utom 0, vilket kan uttryckas med hjälp av intervallnotation på följande sätt: (-∞,0)∪(0,∞).
