Grundfunktionen
In diesem Abschnitt werden wir sieben Grundfunktionen grafisch darstellen, die in diesem Kurs verwendet werden. Jede Funktion wird durch das Einzeichnen von Punkten grafisch dargestellt. Denken Sie daran, dass f(x)=y und somit f(x) und y austauschbar sind.
Jede Funktion der Form f(x)=c, wobei c eine beliebige reelle Zahl ist, nennt man eine konstante FunktionJede Funktion der Form f(x)=c, wobei c eine reelle Zahl ist… Konstante Funktionen sind linear und können mit f(x)=0x+c geschrieben werden. In dieser Form ist es klar, dass die Steigung 0 und der y-Achsenabschnitt (0,c) ist. Die Auswertung eines beliebigen Wertes für x, z. B. x = 2, ergibt c.
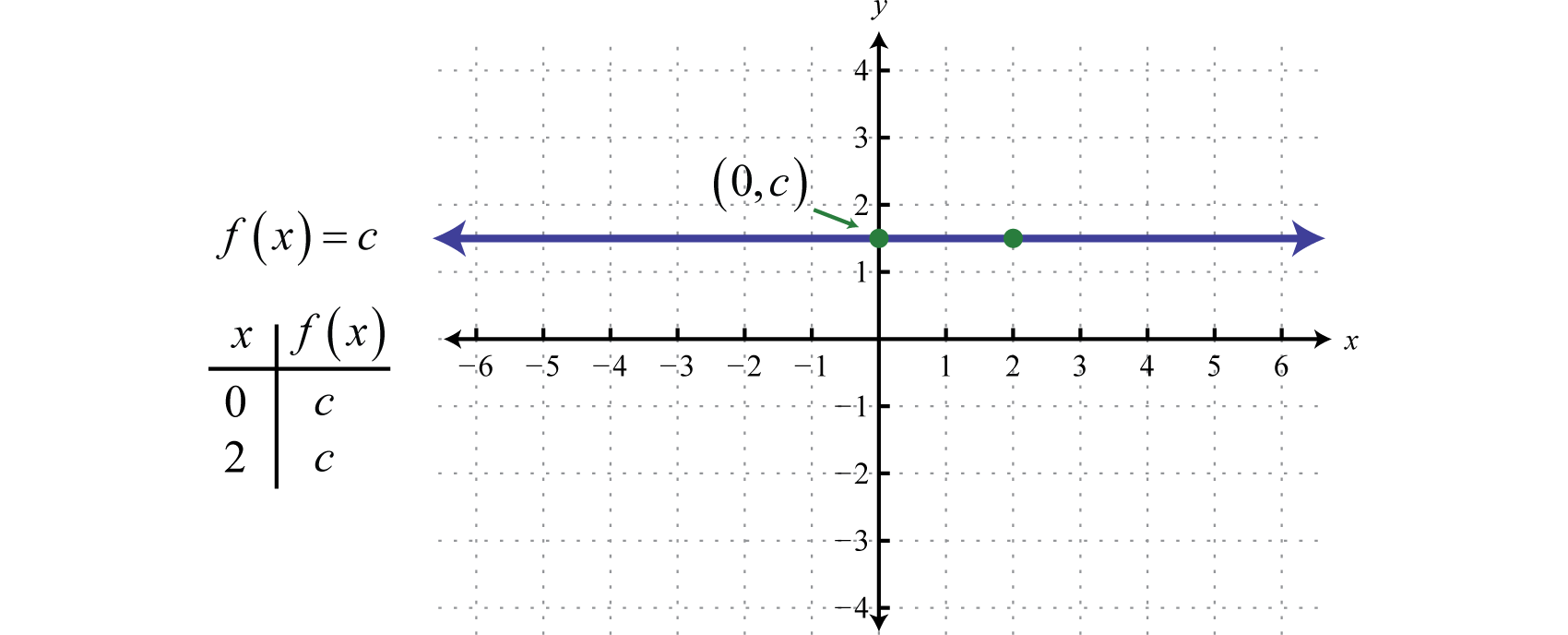
Der Graph einer konstanten Funktion ist eine horizontale Linie. Der Bereich besteht aus allen reellen Zahlen ℝ und der Bereich besteht aus dem einzigen Wert {c}.
Als nächstes definieren wir die IdentitätsfunktionDie lineare Funktion, die durch f(x)=x definiert ist. f(x)=x. Die Auswertung eines beliebigen Wertes für x ergibt denselben Wert. Zum Beispiel: f(0)=0 und f(2)=2. Die Identitätsfunktion ist linear, f(x)=1x+0, mit der Steigung m=1 und dem y-Achsenabschnitt (0, 0).
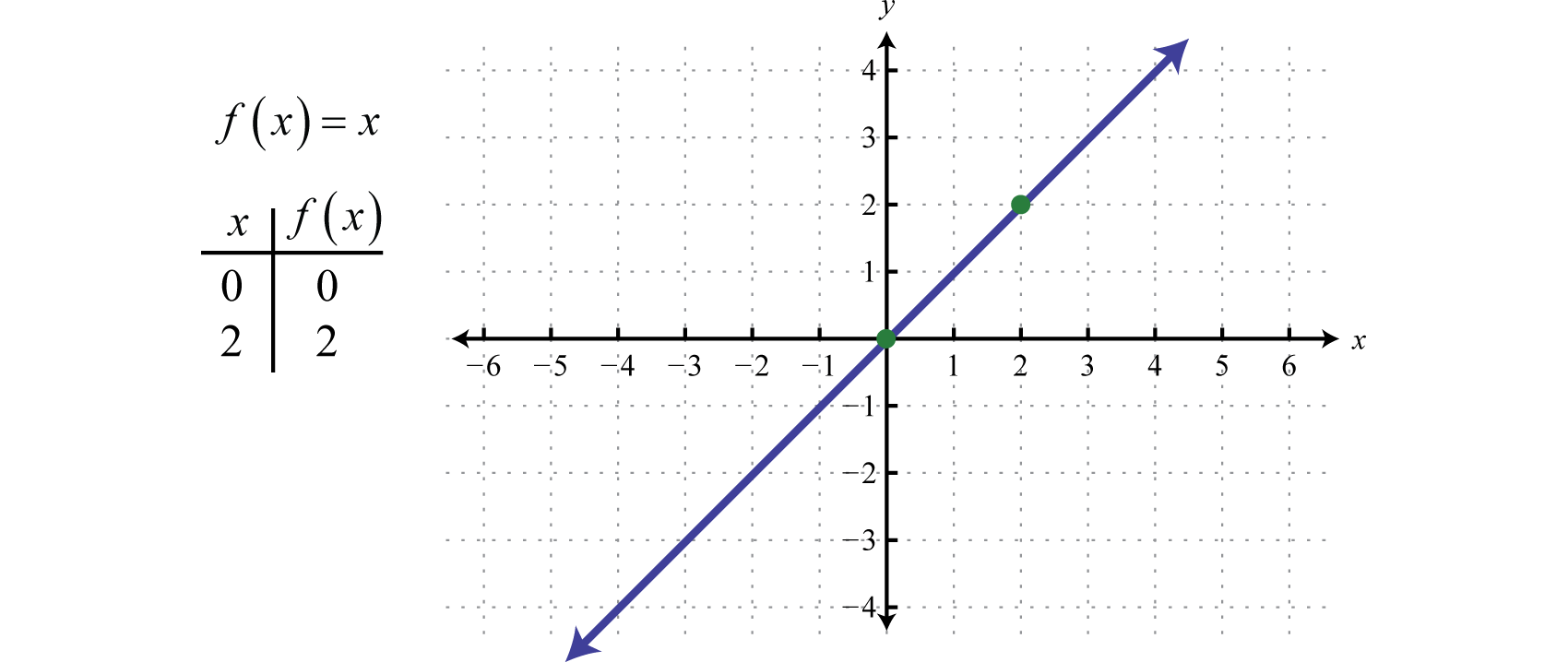
Das Gebiet und der Bereich bestehen beide aus allen reellen Zahlen.
Die QuadrierungsfunktionDie quadratische Funktion, definiert durch f(x)=x2, ist die Funktion, die man durch Quadrieren der Werte im Gebiet erhält. Zum Beispiel: f(2)=(2)2=4 und f(-2)=(-2)2=4. Das Ergebnis der Quadrierung von Werten, die nicht Null sind, ist immer positiv.
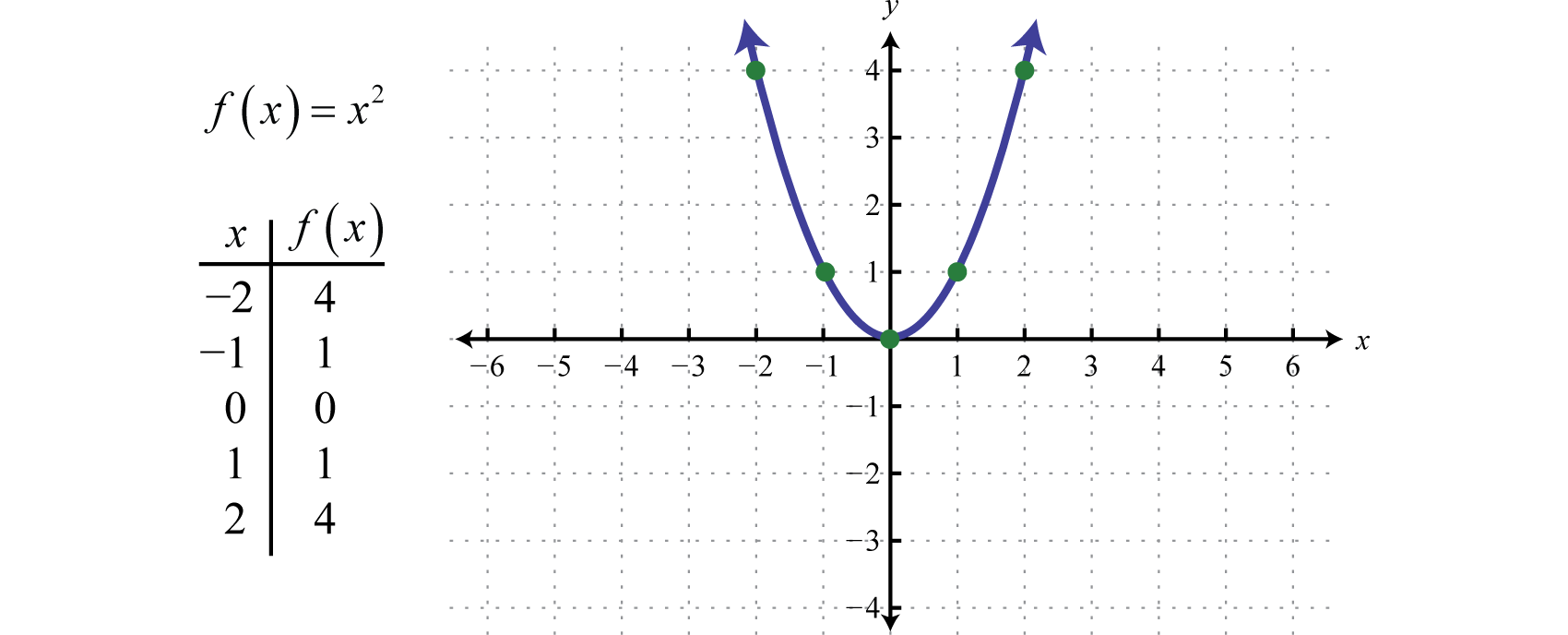
Der resultierende gekrümmte Graph wird als Parabel bezeichnetDer gekrümmte Graph, der durch die Quadrierungsfunktion gebildet wird.. Der Bereich besteht aus allen reellen Zahlen ℝ und der Bereich besteht aus allen y-Werten größer oder gleich Null [0,∞).
Die KubikfunktionDie Kubikfunktion, definiert durch f(x)=x3., definiert durch f(x)=x3, erhöht alle Werte im Bereich auf die dritte Potenz. Die Ergebnisse können entweder positiv, null oder negativ sein. Zum Beispiel ist f(1)=(1)3=1, f(0)=(0)3=0 und f(-1)=(-1)3=-1.
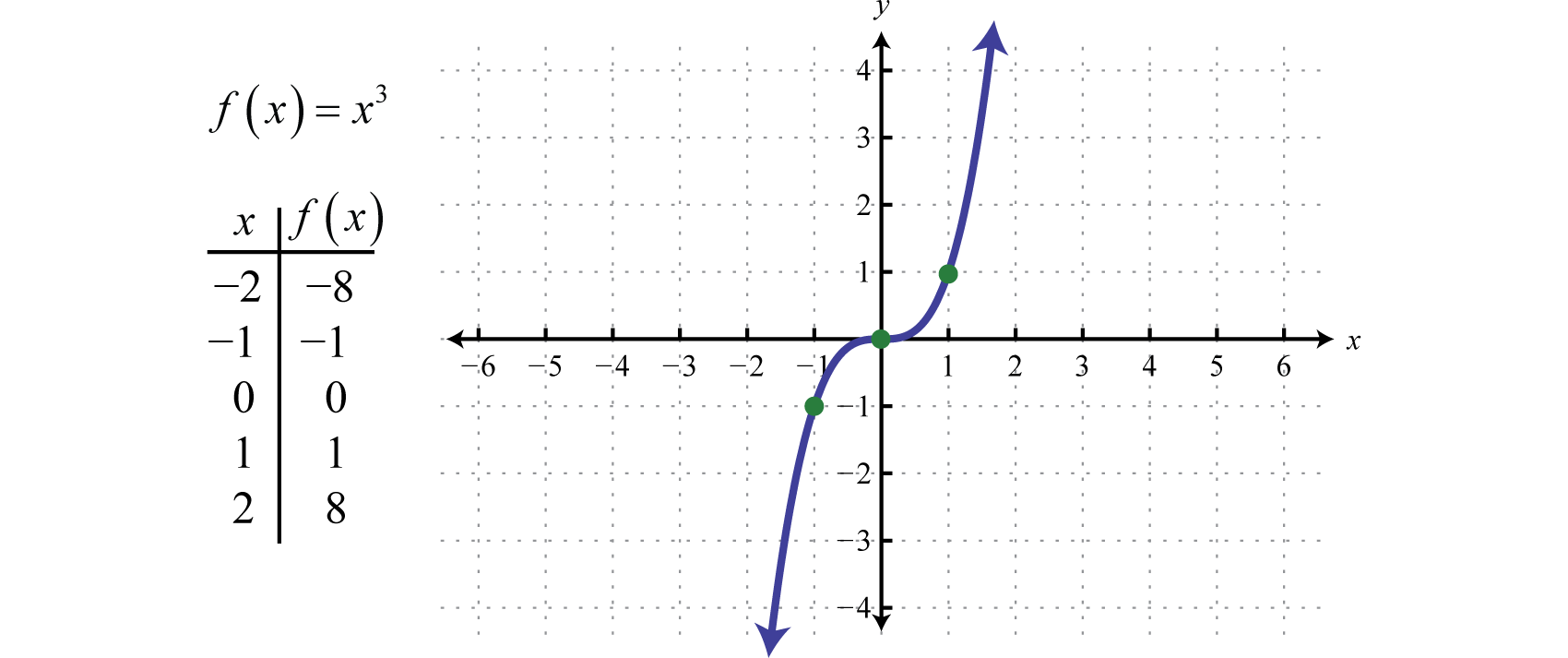
Der Bereich und die Domäne bestehen beide aus allen reellen Zahlen ℝ.
Beachte, dass die Konstante, die Identitäts-, die Quadrier- und die Kubikfunktion alles Beispiele für grundlegende Polynomfunktionen sind. Die nächsten drei Grundfunktionen sind keine Polynome.
Die AbsolutwertfunktionDie Funktion, die durch f(x)=|x| definiert ist, ist eine Funktion, bei der die Ausgabe den Abstand zum Ursprung auf einer Zahlengeraden darstellt. Das Ergebnis der Auswertung der Absolutwertfunktion für jeden Wert von x, der nicht Null ist, ist immer positiv. Zum Beispiel f(-2)=|-2|=2 und f(2)=|2|=2.
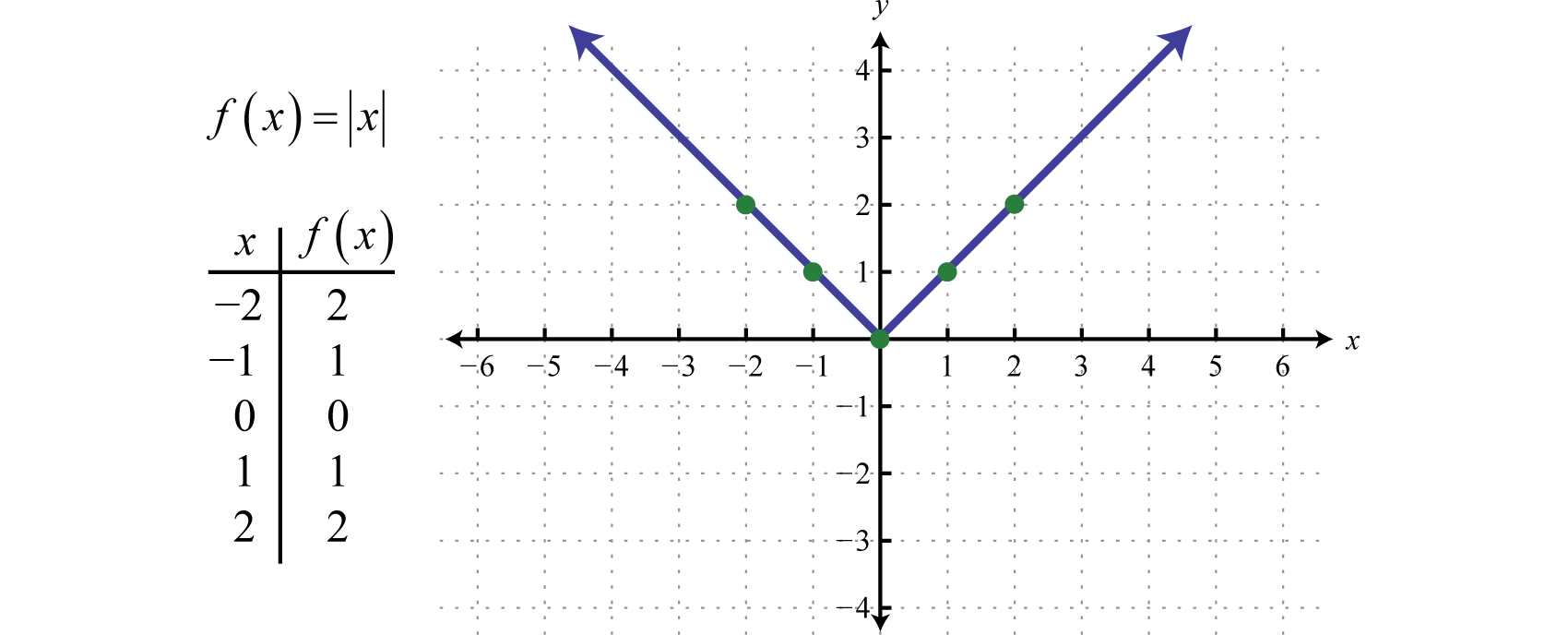
Der Bereich der Absolutwertfunktion besteht aus allen reellen Zahlen ℝ und der Bereich besteht aus allen y-Werten größer oder gleich Null [0,∞).
Die QuadratwurzelfunktionDie Funktion, die durch f(x)=x, definiert durch f(x)=x, ist nicht als reelle Zahl definiert, wenn die x-Werte negativ sind. Daher ist der kleinste Wert im Bereich Null. Zum Beispiel ist f(0)=0=0 und f(4)=4=2.
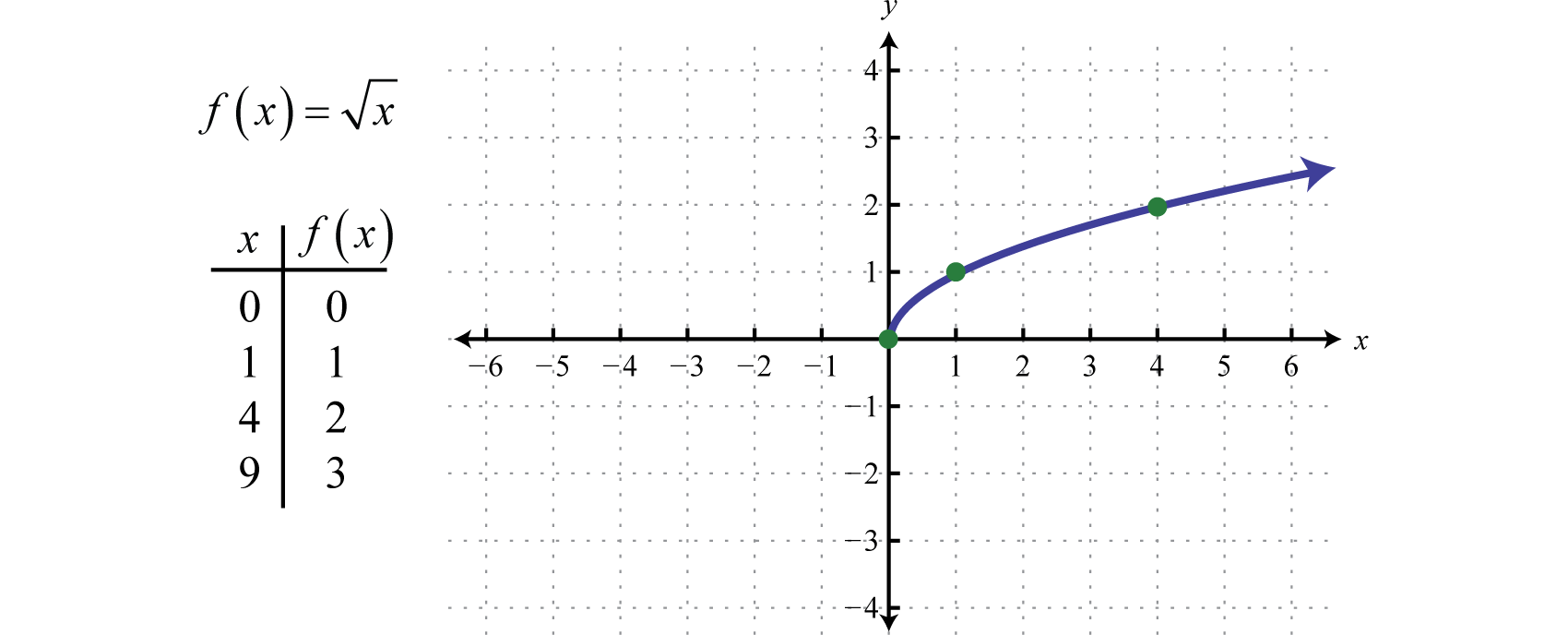
Das Gebiet und der Bereich bestehen beide aus reellen Zahlen größer oder gleich Null [0,∞).
Die KehrwertfunktionDie durch f(x)=1x. definierte Funktion, definiert durch f(x)=1x, ist eine rationale Funktion mit einer Einschränkung auf das Gebiet, nämlich x≠0. Der Kehrwert eines x-Wertes, der sehr nahe bei Null liegt, ist sehr groß. Zum Beispiel,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1.000)=1(11.000)=1⋅1.0001=1.000
Mit anderen Worten, wenn die x-Werte sich Null nähern, tendieren ihre Kehrwerte entweder gegen positive oder negative Unendlichkeit. Dies beschreibt eine vertikale AsymptoteEine vertikale Linie, der sich ein Graph unendlich stark nähert. auf der y-Achse. Außerdem ist das Ergebnis der Kehrwertfunktion sehr klein, wenn die x-Werte sehr groß sind.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11.000=0,001
Mit anderen Worten: Wenn die x-Werte sehr groß werden, tendieren die resultierenden y-Werte gegen Null. Dies beschreibt eine horizontale AsymptoteEine horizontale Linie, zu der ein Graph unendlich nahe kommt, wenn die x-Werte gegen ±∞ tendieren. auf der x-Achse. Nach dem Auftragen einer Reihe von Punkten kann die allgemeine Form der Kehrwertfunktion bestimmt werden.
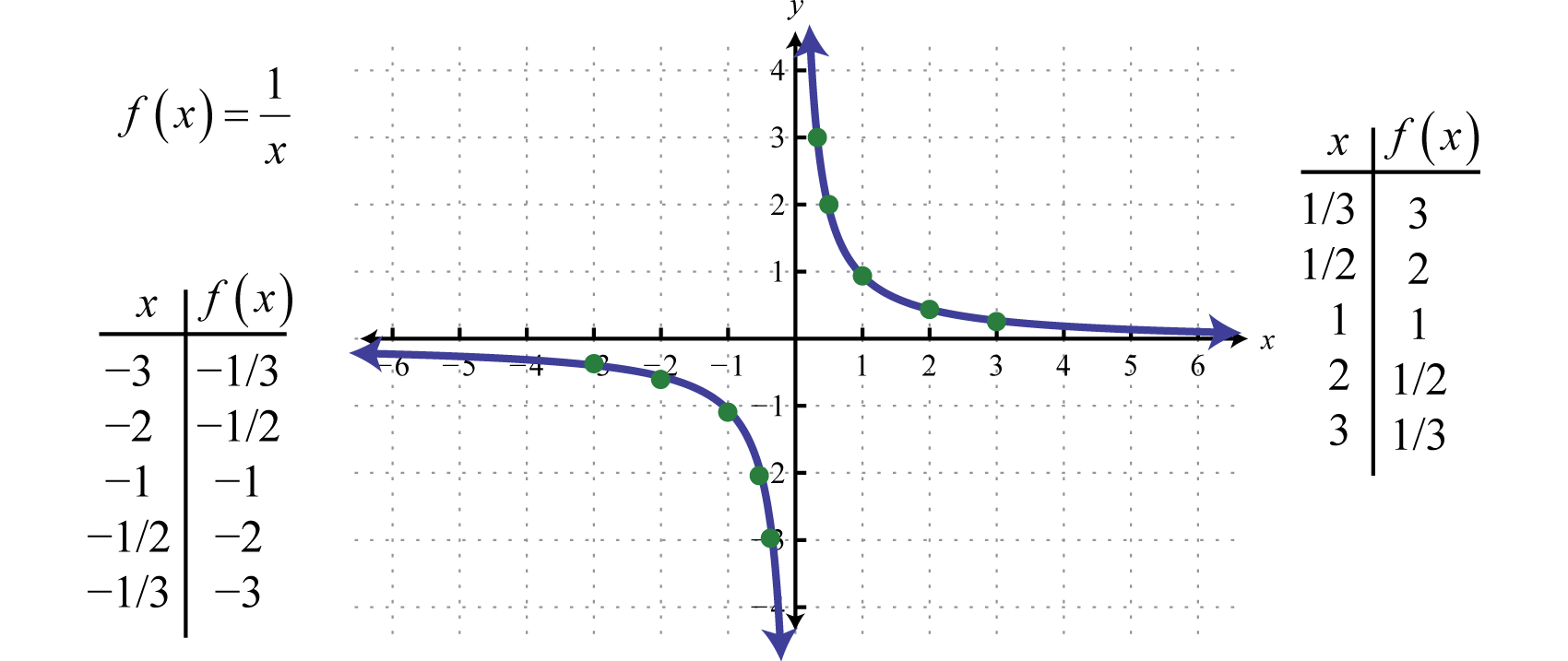
Bei der Kehrwertfunktion bestehen sowohl der Bereich als auch der Bereich aus allen reellen Zahlen außer 0, was mit Hilfe der Intervallnotation wie folgt ausgedrückt werden kann: (-∞,0)∪(0,∞).
