基本関数
このセクションでは、このコースを通して使用される7つの基本関数をグラフ化します。 各関数は点をプロットしてグラフ化します。 f(x)=yなので、f(x)とyは入れ替えて使えることを覚えておいてください。
cが任意の実数で、f(x)=cの形の任意の関数は、定数関数と呼ばれますcが実数でf(x)=cの形の任意の関数は…。 定数関数は線形であり、f(x)=0x+cと書くことができる。 この形では、傾きが0、y切片が(0,c)であることは明らかである。 x=2のようにxの任意の値を評価するとcになります。
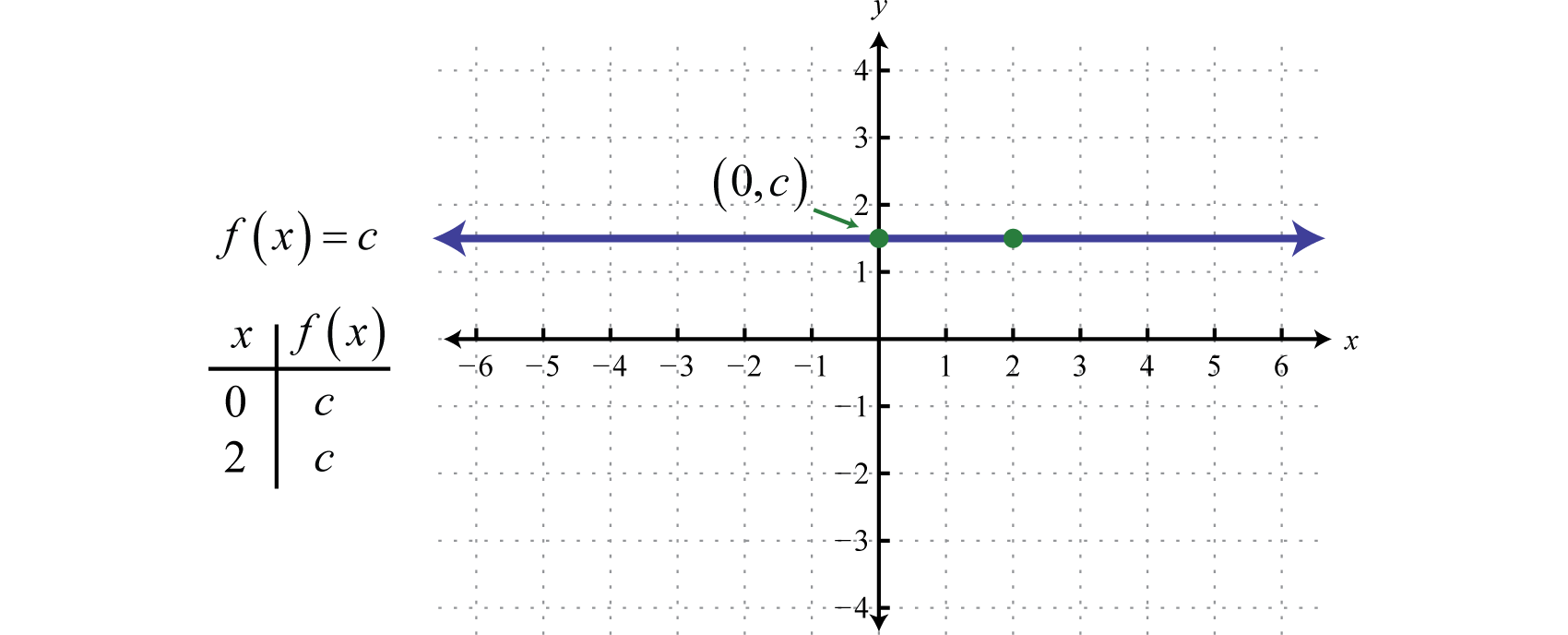
定数関数のグラフは水平線になります。 領域はすべての実数ℝからなり、範囲は単一の値{c}からなる。
次に恒等関数f(x)=xで定義される線形関数を定義する。 xに対して任意の値を評価すると、その同じ値になる。 例えば、f(0)=0、f(2)=2です。 恒等関数は一次関数で、f(x)=1x+0、傾きm=1、y切片(0、0)である。
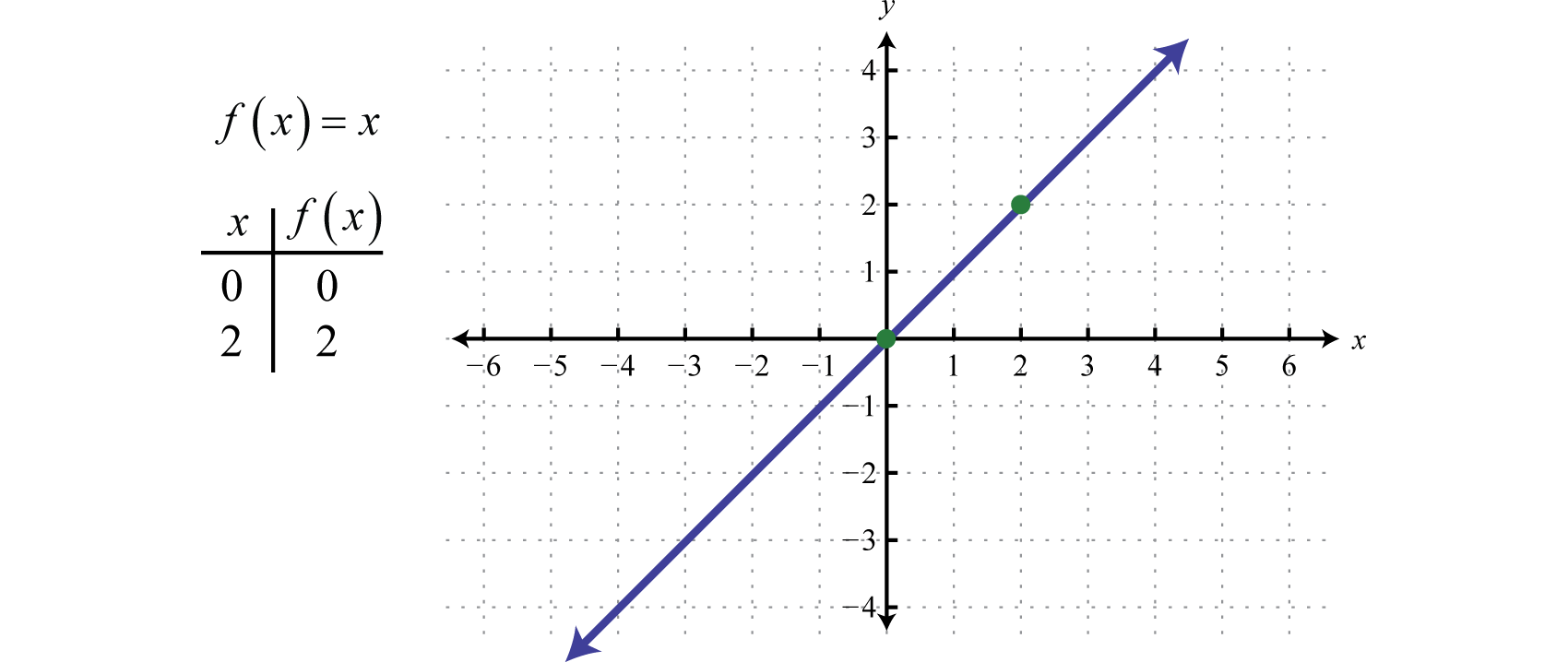
領域と範囲はともにすべての実数からなる。
二乗関数f(x)=x2.によって定義されている二次関数とは領域の値を二乗して得られる関数である。 例えば、f(2)=(2)2=4、f(-2)=(-2)2=4である。 ドメイン内の0以外の値を2乗した結果は必ず正になる。
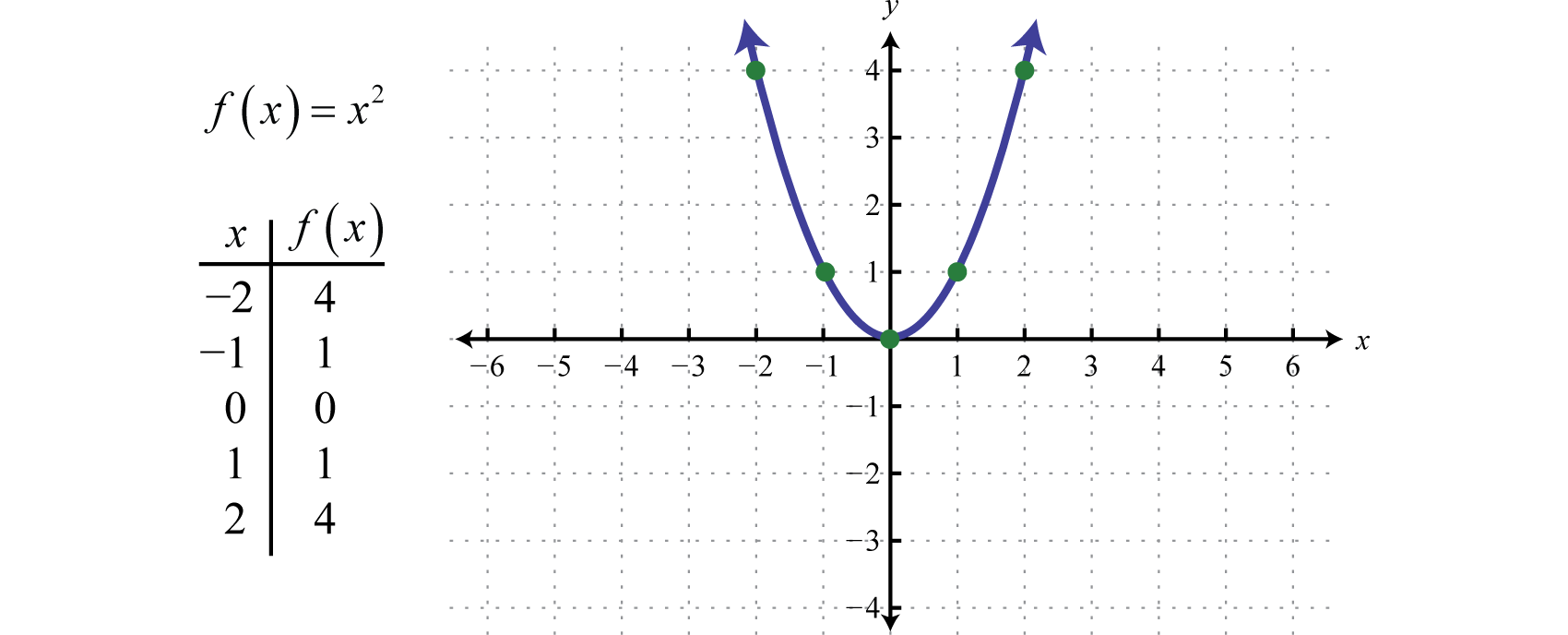
得られる曲線グラフを放物線と呼ぶ2乗関数が形成する曲線グラフは…。 領域はすべての実数ℝ、範囲は0以上のすべてのy値[0,∞]からなる。
三乗関数f(x)=x3によって定義される三乗関数は、領域のすべての値を3乗に引き上げる。 結果は正、0、負のいずれかになる。 例えば、f(1)=(1)3=1、f(0)=(0)3=0、f(-1)=(-1)3=-1となる。
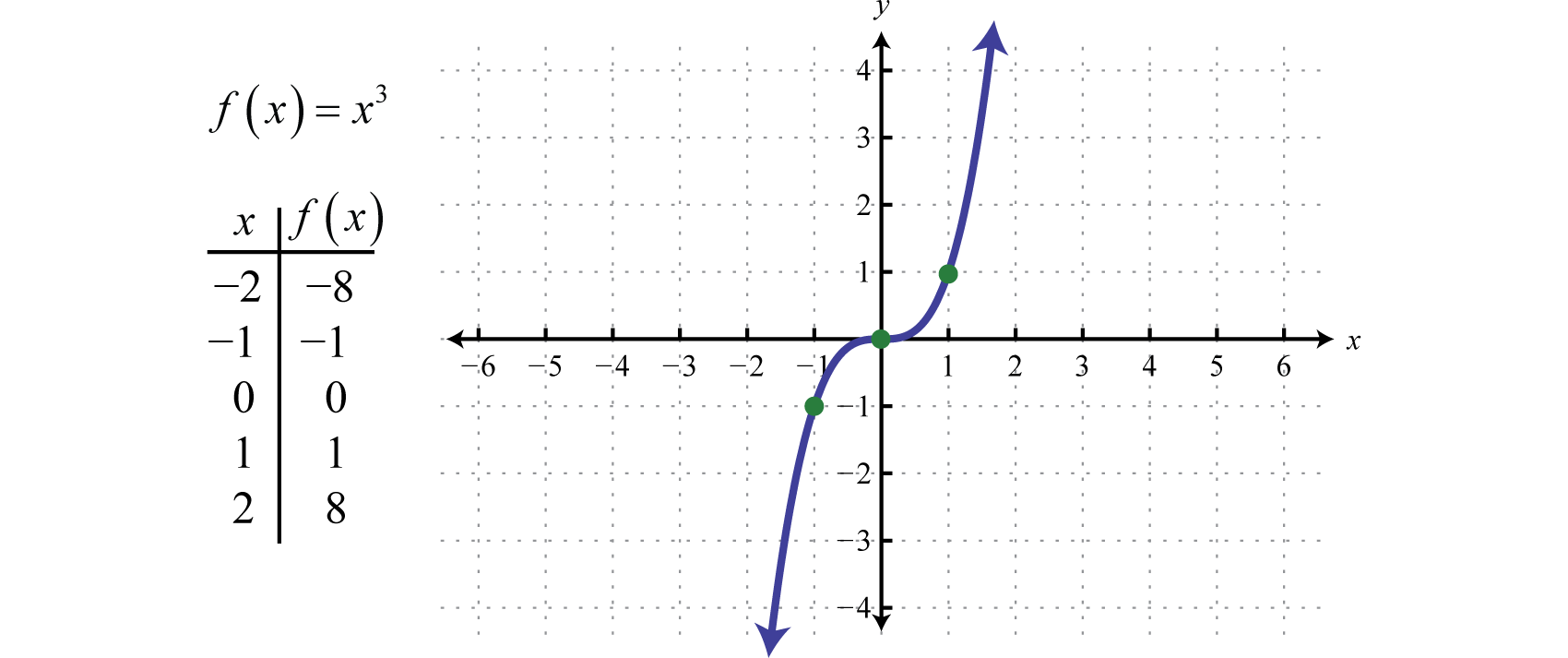
領域と範囲は両方ともすべての実数ℝからなる。
定数と等式、2乗および3乗はすべて基本の多項式機能の例であることに注意してください。 次の3つの基本的な関数は多項式ではない。
絶対値関数f(x)=|x|.で定義される関数は、出力が数直線上の原点への距離を表す関数である。 絶対値関数をゼロ以外の値xについて評価した結果は、必ず正の値になります。 例えば、f(-2)=|-2|=2、f(2)=|2|=2。
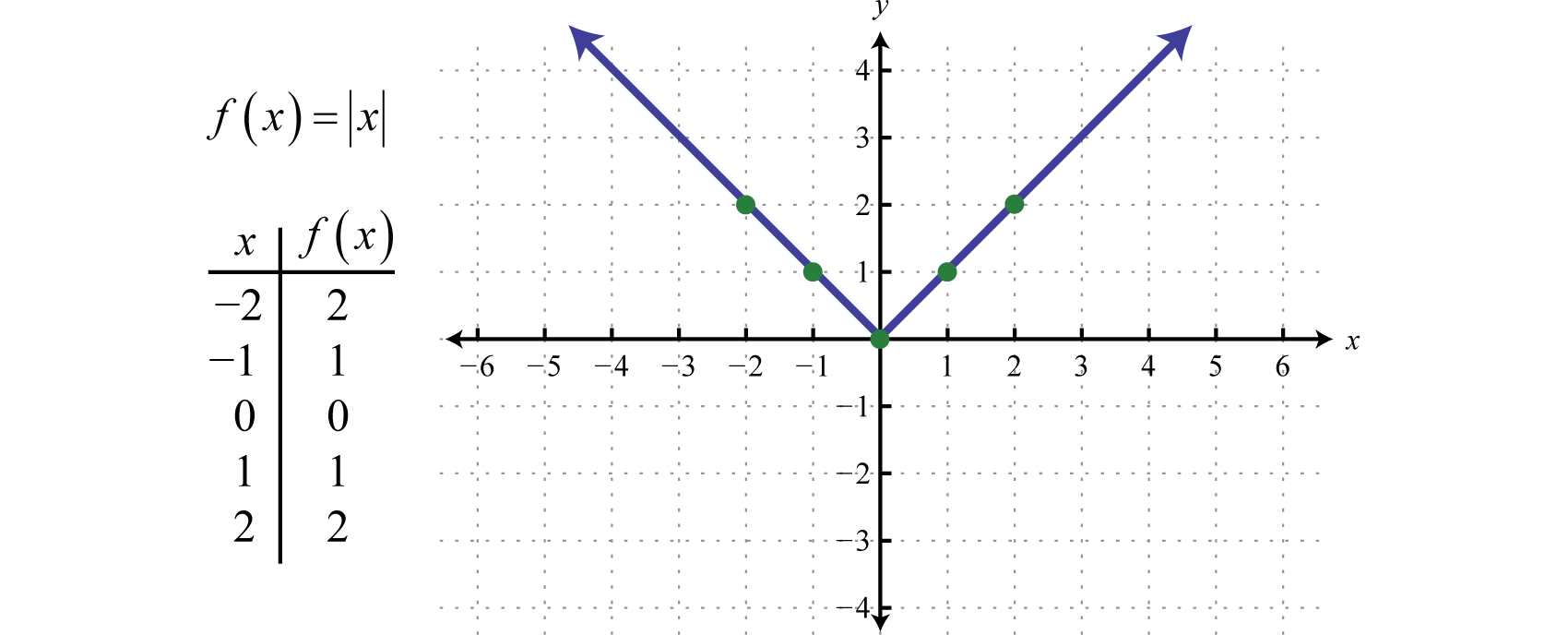
絶対値関数のドメインはすべての実数ℝからなり、範囲はゼロ以上のすべてのy値 [0,∞) から構成されます。 f(x)=x.で定義される関数は、x値が負の場合は実数であると定義されない。 したがって、領域内の最小値は0となる。 例えば、f(0)=0、f(4)=4=2。
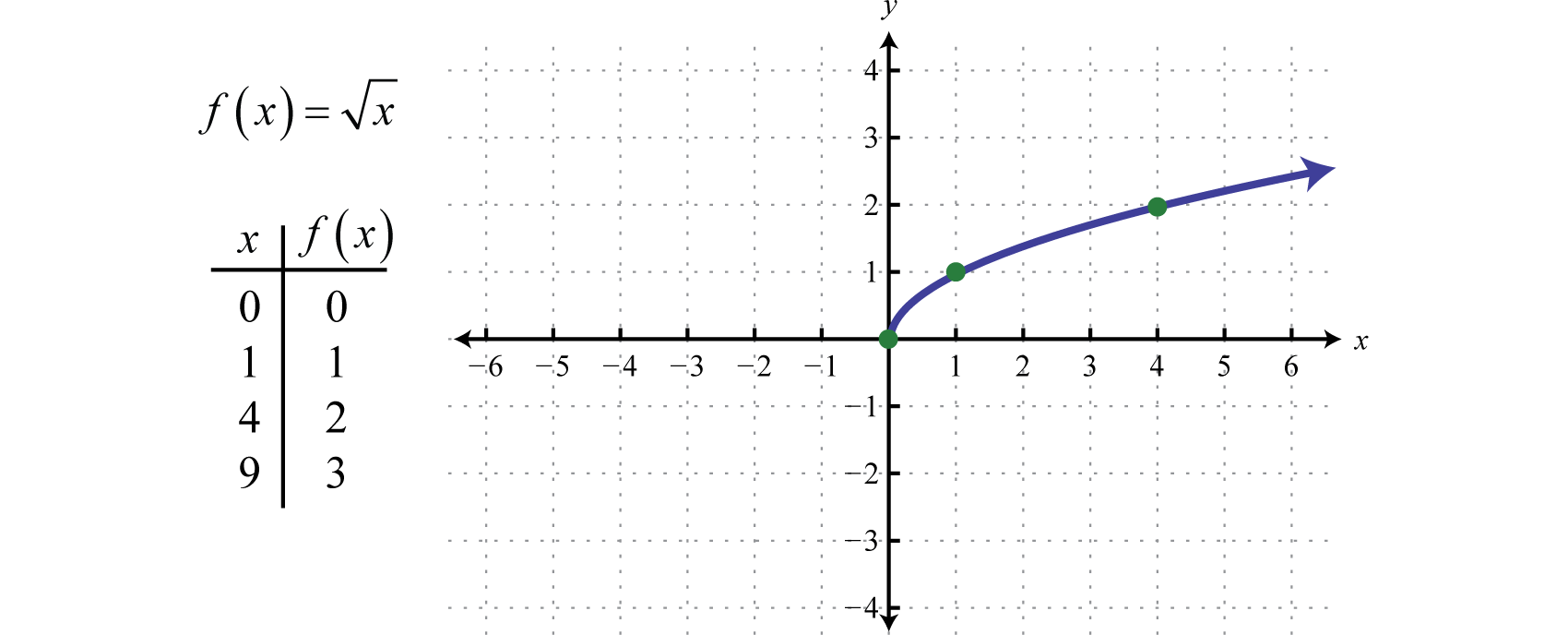
領域と範囲はともにゼロ以上の実数からなる [0,∞].
逆関数f(x)=1x.によって定義される関数は、領域上に一つの制限、すなわち x≠0 を持つ有理関数である。 ゼロに非常に近いx値の逆数は非常に大きい。 例えば、
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1,000)=1(11,000)=1⋅1,0001=1,000 つまりx値が0に近づくとその逆数は正または負の無限大の方向に傾くことになる。 これは垂直漸近線と呼ばれるもので、グラフが無限に近くなる垂直線をy軸に描いている。
f(10)=110=0.1f(100)=1100=0.01f(1000)=11000=0.001
言い換えれば、x値が非常に大きくなると、結果のy値は0に近づく傾向がある。 これは水平漸近線と呼ばれるもので、x値をx軸として±∞の方向に限りなく近づける水平線です。
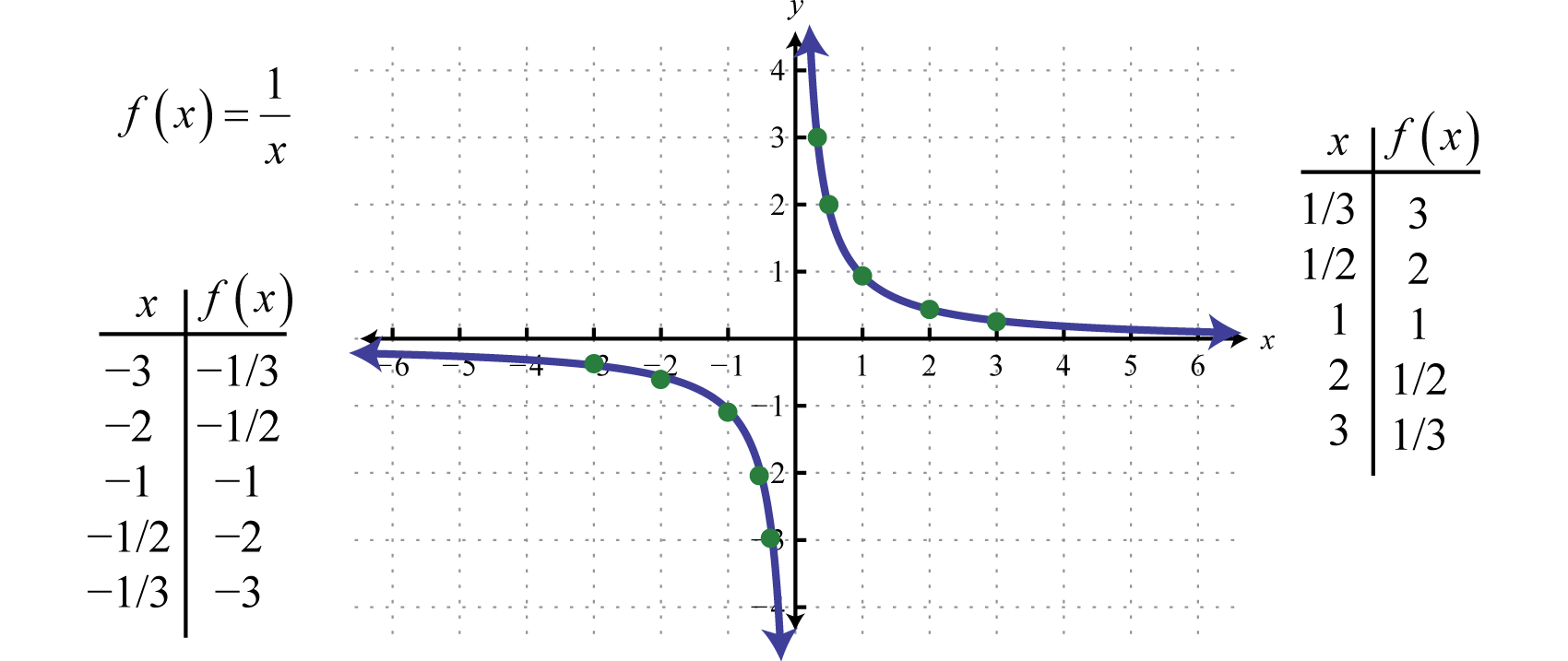
逆関数の領域と範囲は0を除くすべての実数からなり、区間表記で次のように表わすことができる。 (-∞,0)∪(0,∞).
