Funções Básicas
Nesta seção, nós mostramos um gráfico de sete funções básicas que serão utilizadas ao longo deste curso. Cada função é graficada através de pontos de plotagem. Lembre-se que f(x)=y e assim f(x) e y podem ser usados intercambiavelmente.
Ainda função da forma f(x)=c, onde c é qualquer número real, é chamada uma função constanteAinda função da forma f(x)=c onde c é um número real… As funções constantes são lineares e podem ser escritas f(x)=0x+c. Nesta forma, é claro que a inclinação é 0 e o intercepção y é (0,c). Avaliando qualquer valor para x, como x = 2, resultará em c.
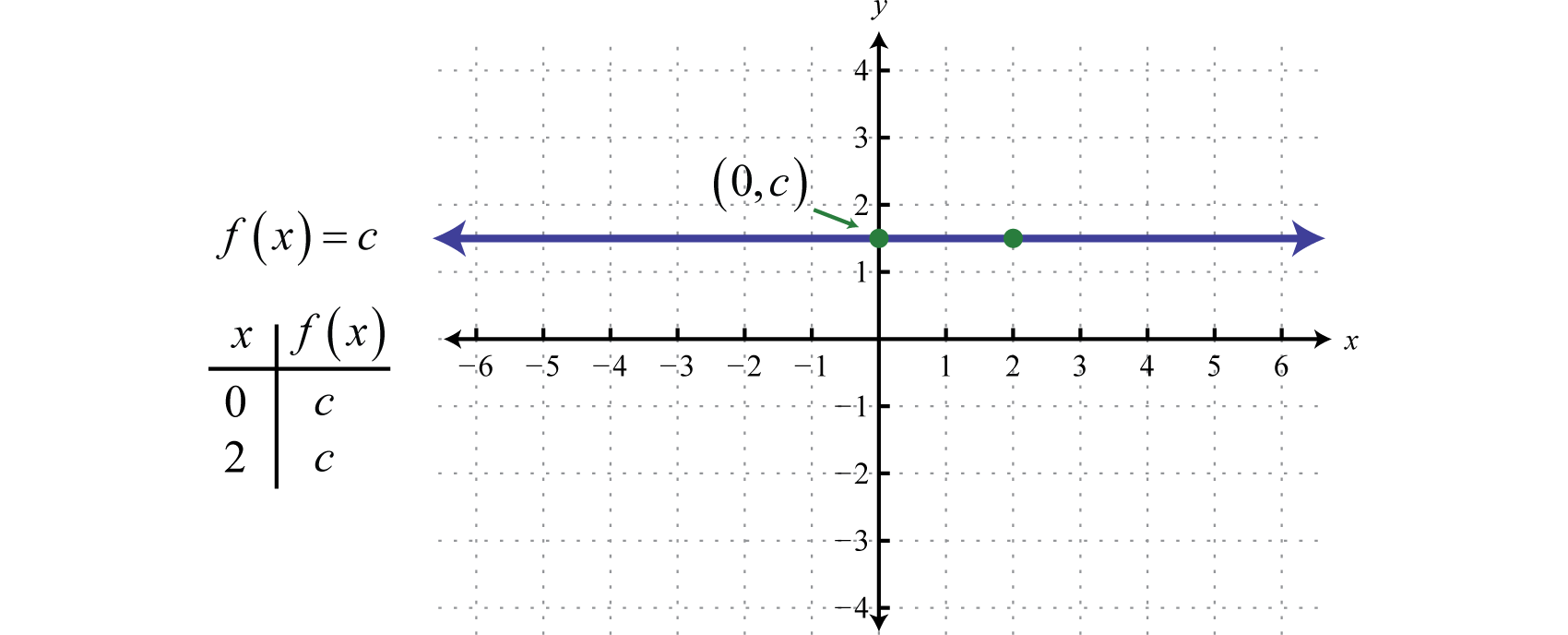
O gráfico de uma função constante é uma linha horizontal. O domínio consiste em todos os números reais ℝ e o intervalo consiste no valor único {c}.
A seguir definimos a função de identidadeA função linear definida por f(x)=x. f(x)=x. Avaliar qualquer valor para x resultará nesse mesmo valor. Por exemplo, f(0)=0 e f(2)=2. A função de identificação é linear, f(x)=1x+0, com inclinação m=1 e intercepção y (0, 0).
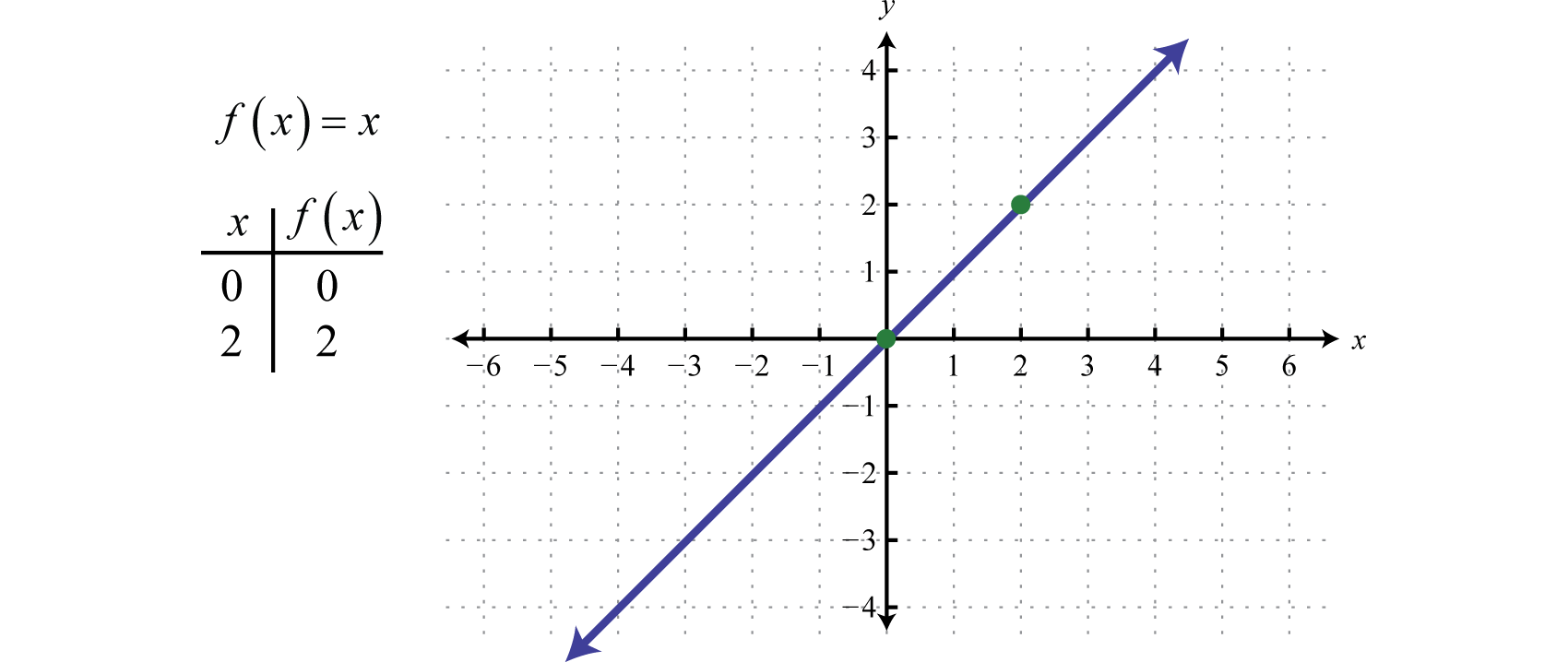
O domínio e o intervalo consistem em todos os números reais.
A função quadrática A função quadrática definida por f(x)=x2., definida por f(x)=x2, é a função obtida pela quadratura dos valores no domínio. Por exemplo, f(2)=(2)2=4 e f(-2)=(-2)2=4. O resultado do quadrado de valores não zero no domínio será sempre positivo.
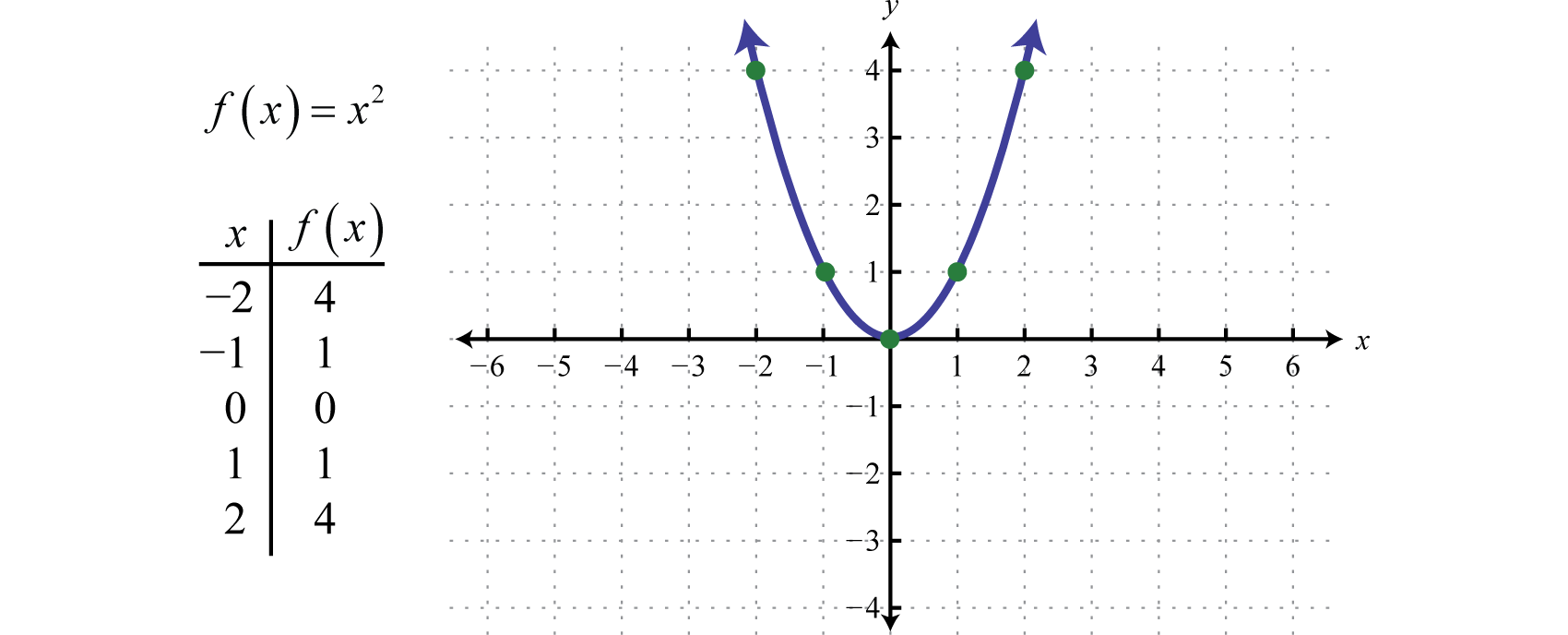
O gráfico curvo resultante é chamado de parábolaO gráfico curvo formado pela função de quadrado… O domínio consiste em todos os números reais ℝ e o intervalo consiste em todos os valores y maiores ou iguais a zero [0,∞).
A função de cubicaçãoA função cúbica definida por f(x)=x3., definida por f(x)=x3, eleva todos os valores do domínio para a terceira potência. Os resultados podem ser ou positivos, zero, ou negativos. Por exemplo, f(1)=(1)3=1, f(0)=(0)3=0, e f(-1)=(-1)3=-1.
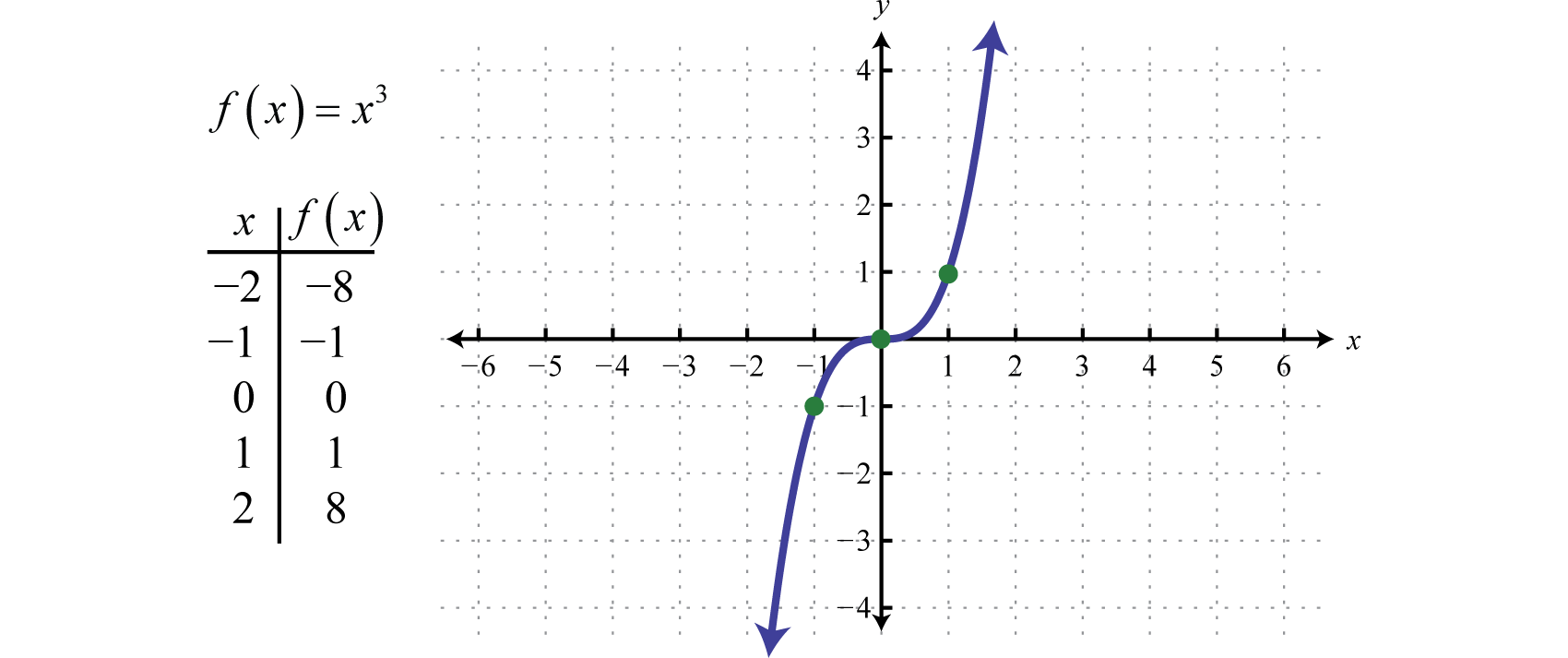
O domínio e o intervalo consistem de todos os números reais ℝ.
Notem que as funções constante, identidade, quadrado e cubo são todos exemplos de funções polinomiais básicas. As próximas três funções básicas não são polinomiais.
A função valor absolutoA função definida por f(x)=|x|., definida por f(x)=|x|, é uma função onde a saída representa a distância à origem em uma linha numérica. O resultado da avaliação da função de valor absoluto para qualquer valor não nulo de x será sempre positivo. Por exemplo, f(-2)=|-2|=2 e f(2)=|2|=2.
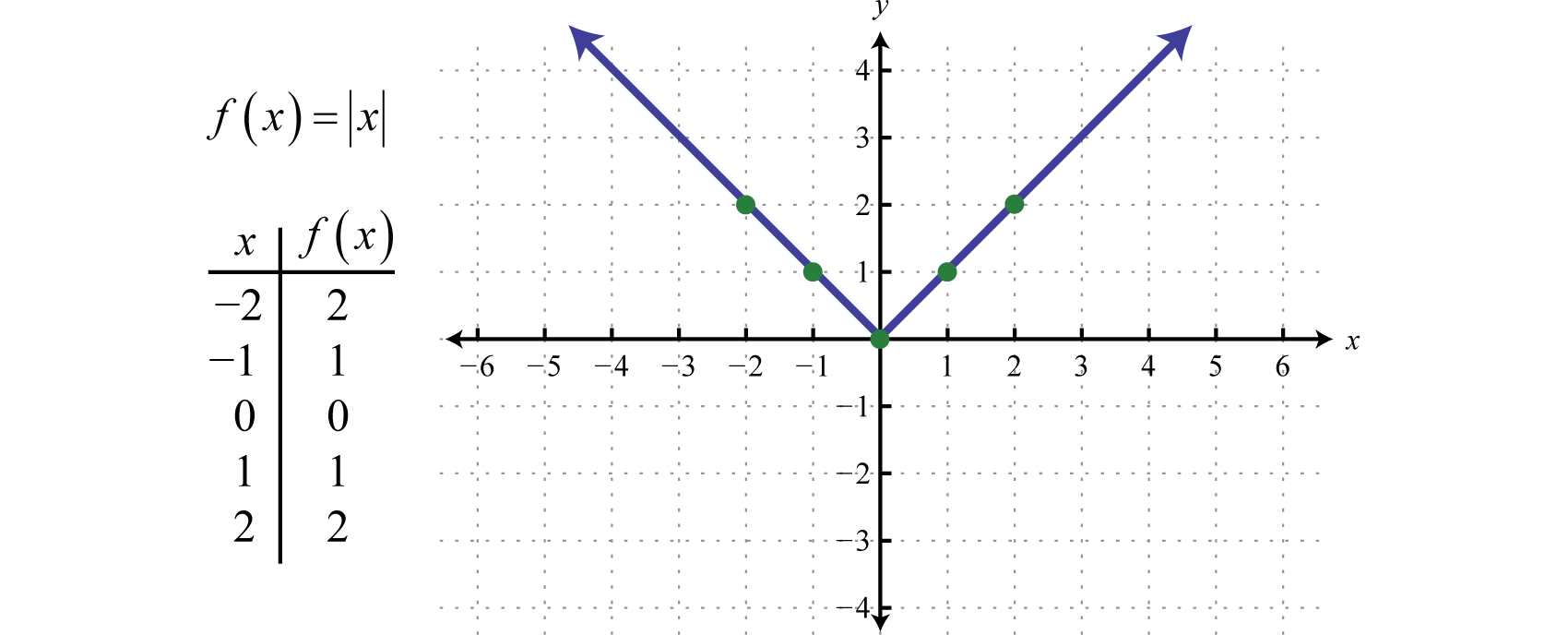
O domínio da função valor absoluto consiste em todos os números reais ℝ e o intervalo consiste em todos os valores y maiores ou iguais a zero [0,∞).
A função raiz quadradaA função definida por f(x)=x, definida por f(x)=x, não está definida para ser um número real se os valores x forem negativos. Portanto, o menor valor no domínio é zero. Por exemplo, f(0)=0=0 e f(4)=4=2.
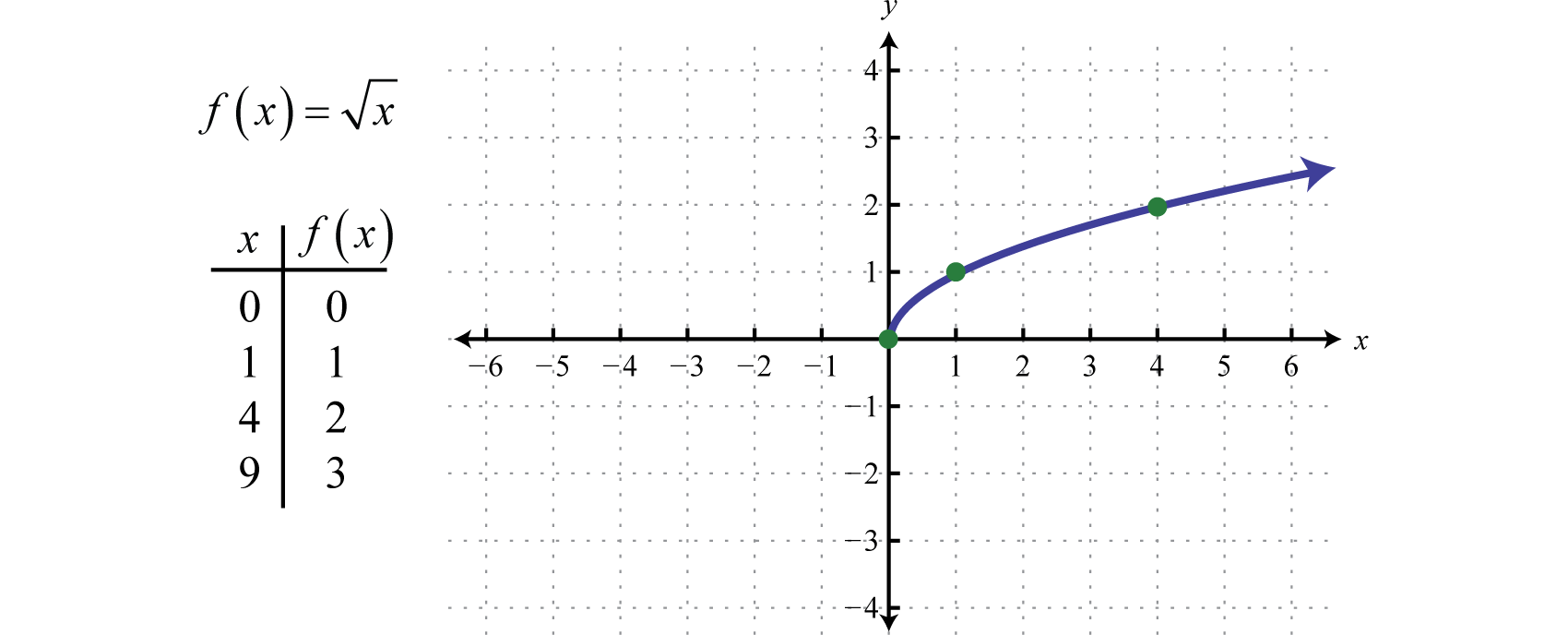
O domínio e o intervalo consistem em números reais maiores ou iguais a zero [0,∞).
A função recíprocaA função definida por f(x)=1x., definida por f(x)=1x, é uma função racional com uma restrição no domínio, nomeadamente x≠0. O recíproco de um valor x muito próximo de zero é muito grande. Por exemplo,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1,000)=1(11,000)=1⋅1,0001=1,000
Em outras palavras, à medida que os valores x se aproximam de zero os seus recíprocos tenderão para o infinito positivo ou negativo. Isto descreve uma linha vertical assíntotaA vertical para a qual um gráfico se torna infinitamente próximo. no eixo y. Além disso, onde os valores x são muito grandes o resultado da função recíproca é muito pequeno.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11.000=0,001
Em outras palavras, como os valores x se tornam muito grandes os valores y resultantes tendem para zero. Isto descreve uma linha horizontal assíntotaA horizontal para a qual um gráfico se torna infinitamente próximo onde os valores x tendem para ±∞. no eixo x. Após traçar um número de pontos, a forma geral da função recíproca pode ser determinada.
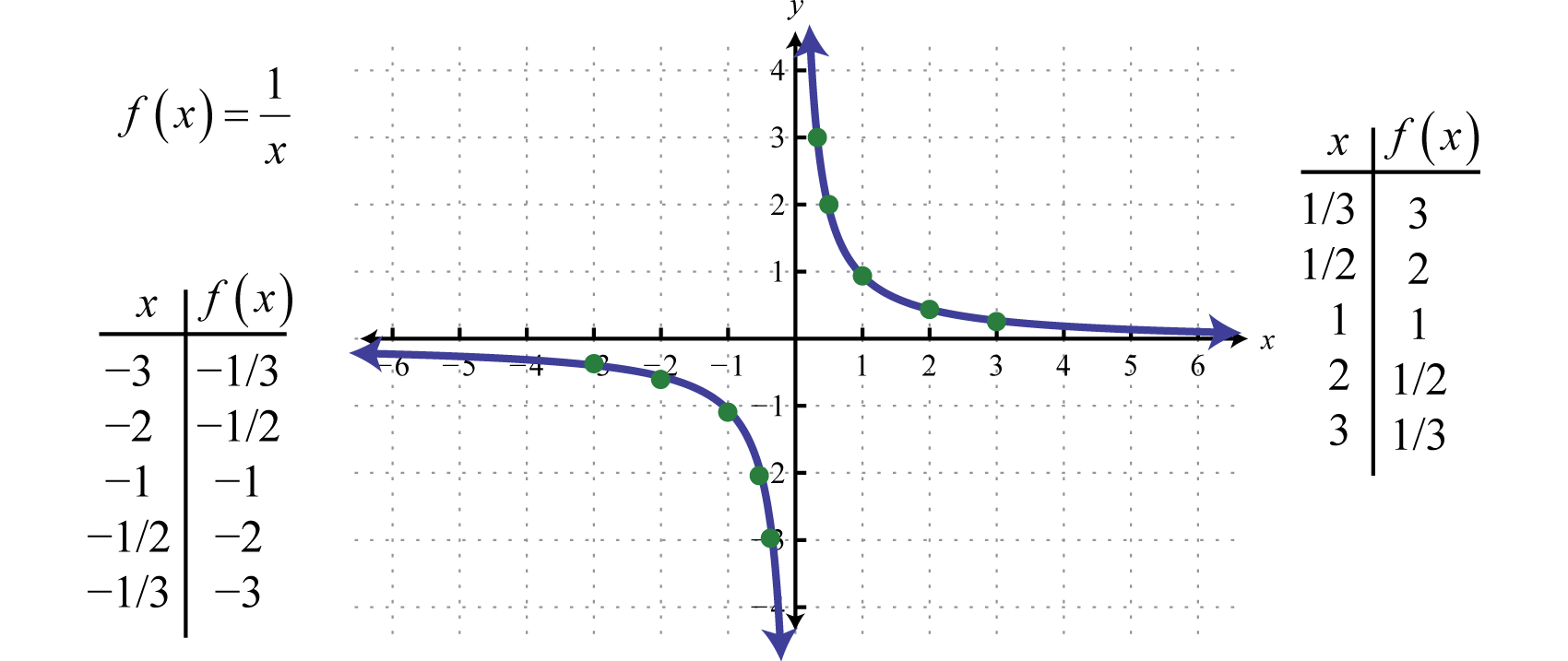
Bambos o domínio e o intervalo da função recíproca consiste em todos os números reais, exceto 0, que podem ser expressos usando notação de intervalo como a seguir: (−∞,0)∪(0,∞).
