Az alapfüggvények
Ebben a részben hét alapfüggvényt grafikusan ábrázolunk, amelyeket az egész kurzus során használni fogunk. Minden egyes függvényt pontok ábrázolásával grafikusan ábrázolunk. Ne feledjük, hogy f(x)=y, és így f(x) és y felcserélhetően használható.
Az f(x)=c alakú függvényt, ahol c egy tetszőleges valós szám, konstans függvénynek nevezzükAz f(x)=c alakú függvényt, ahol c egy valós szám… Az állandó függvények lineárisak és felírhatók f(x)=0x+c. Ebben a formában egyértelmű, hogy a meredekség 0, az y-intercept pedig (0,c). Bármely x érték kiértékelése, például x = 2, c-t eredményez.
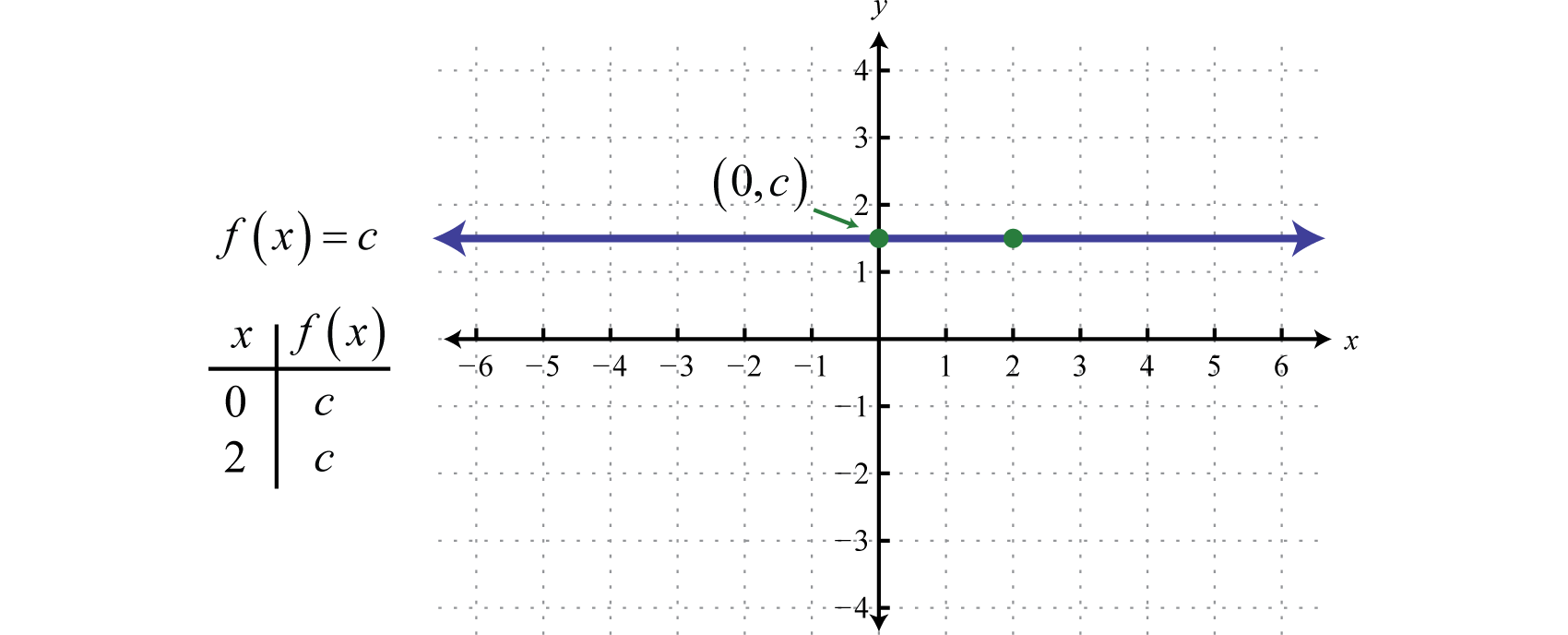
A konstans függvény grafikonja egy vízszintes egyenes. Tartománya az összes ℝ valós számból, tartománya pedig egyetlen értékből {c} áll.
A következőkben definiáljuk az azonossági függvénytA lineáris függvényt, amelyet f(x)=x határoz meg. f(x)=x. Bármely x érték kiértékelése ugyanazt az értéket fogja eredményezni. Például f(0)=0 és f(2)=2. Az azonossági függvény lineáris, f(x)=1x+0, meredeksége m=1, y-interceptusa (0, 0).
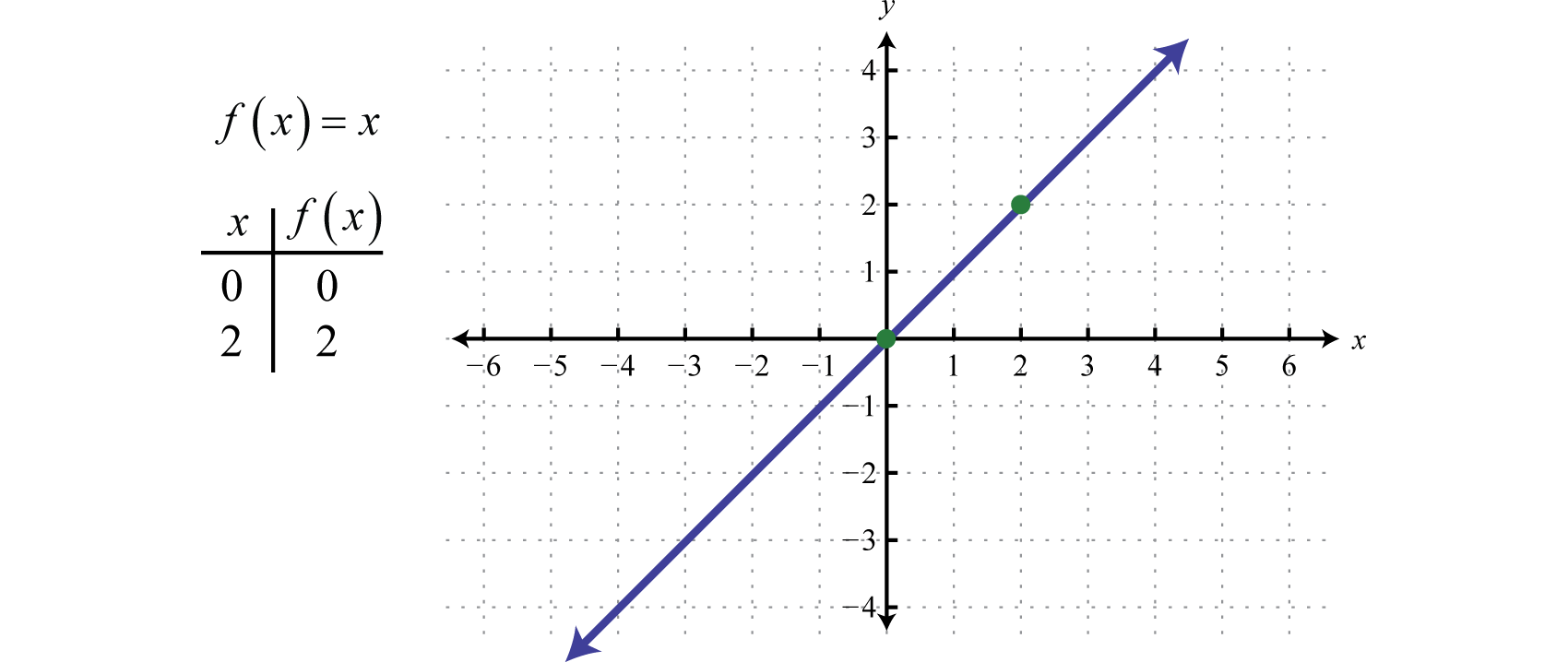
A tartomány és a tartomány is minden valós számból áll.
A négyzetes függvényA f(x)=x2. által definiált négyzetes függvény, f(x)=x2 által definiált függvény, amelyet a tartományban lévő értékek négyzetelésével kapunk. Például f(2)=(2)2=4 és f(-2)=(-2)2=4. A tartományban lévő nem nulla értékek négyzetre emelésének eredménye mindig pozitív lesz.
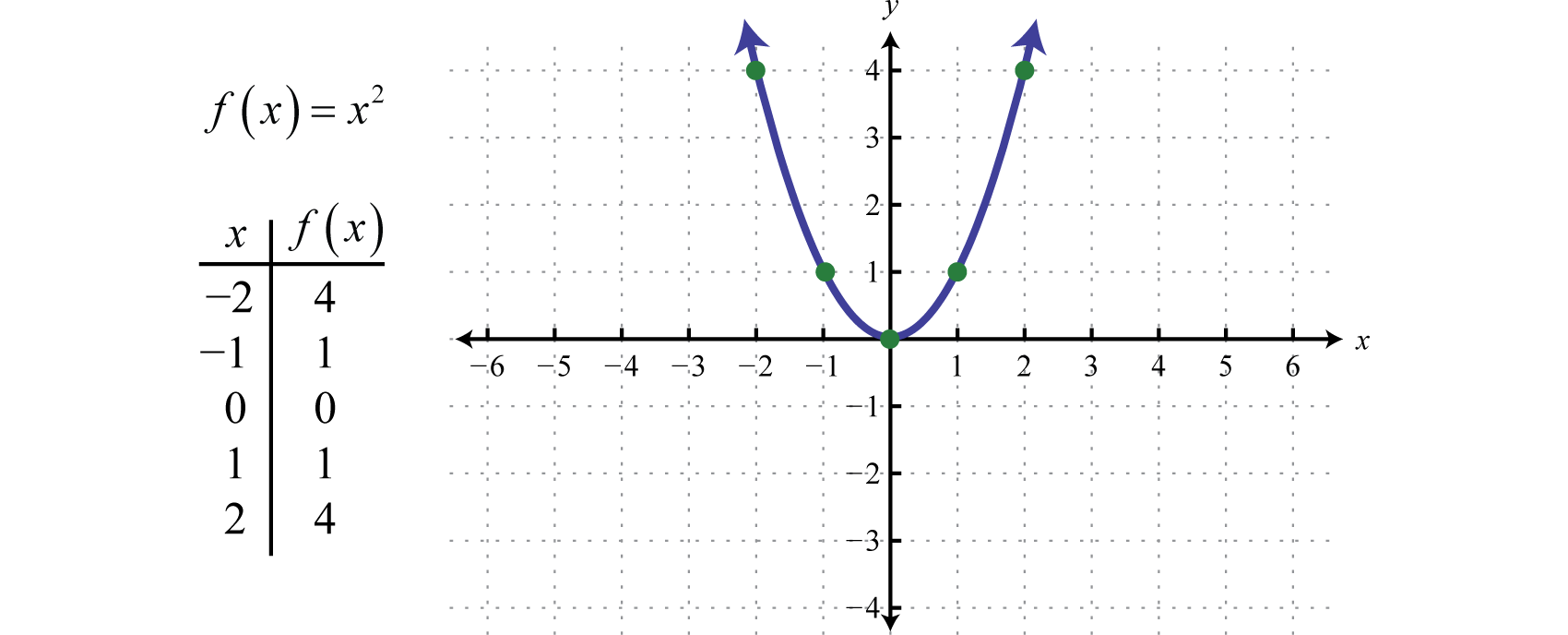
A kapott görbe grafikont parabolának nevezzükA négyzetes függvény által alkotott görbe grafikon… A tartományt az összes ℝ valós szám, a tartományt pedig az összes nullánál nagyobb vagy azzal egyenlő y-érték [0,∞) alkotja.
A köbösítő függvényA f(x)=x3. által meghatározott köbösítő függvény, amelyet f(x)=x3 határoz meg, a tartományban lévő összes értéket a harmadik hatványra emeli. Az eredmény lehet pozitív, nulla vagy negatív. Például f(1)=(1)3=1, f(0)=(0)3=0, és f(-1)=(-1)3=-1.
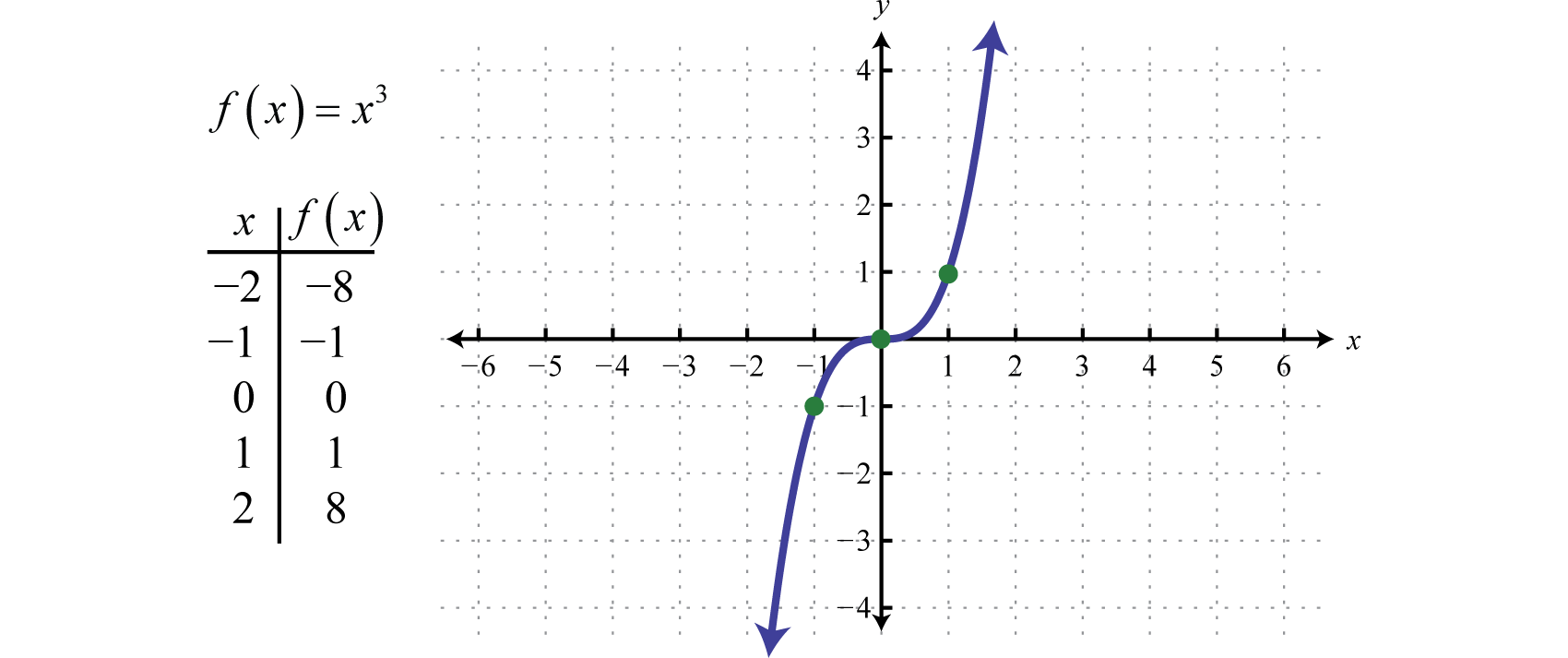
A tartomány és a tartomány is az összes valós számból áll ℝ.
Megjegyezzük, hogy az állandó, az azonosság, a négyzet és a kocka függvények mind az alapvető polinomfüggvények példái. A következő három alapfüggvény nem polinom.
Az abszolútérték-függvényA f(x)=|x|. által definiált f(x)=|x|. által definiált függvény olyan függvény, amelynek kimenete az origótól való távolságot jelenti a számegyenesen. Az abszolútérték-függvény kiértékelésének eredménye x bármely nem nulla értékére mindig pozitív lesz. Például f(-2)=|-2|=2 és f(2)=|2|=2.
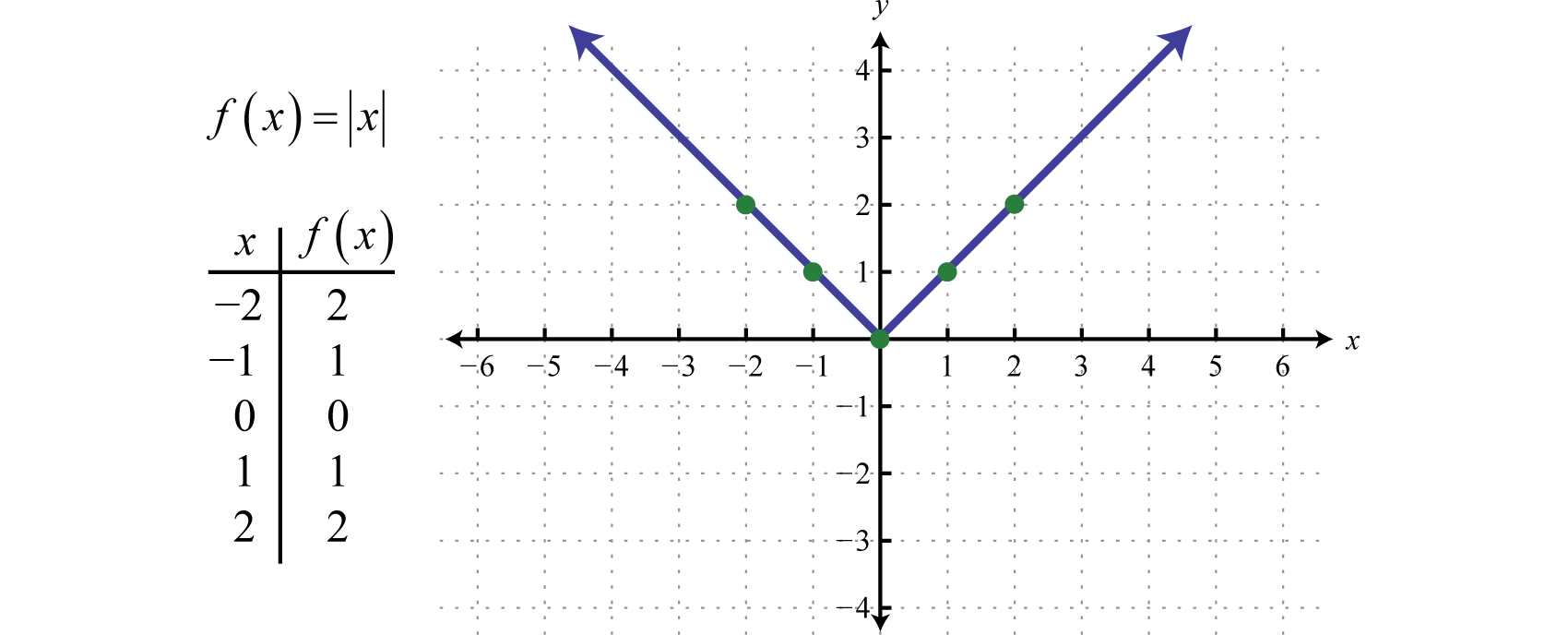
Az abszolútérték-függvény tartománya az összes ℝ valós számból áll, tartománya pedig az összes nullánál nagyobb vagy azzal egyenlő y-értékből [0,∞].
A négyzetgyökfüggvényA f(x)=x által definiált függvény, f(x)=x által definiált négyzete nem valós szám, ha az x-értékek negatívak. Ezért a tartomány legkisebb értéke nulla. Például f(0)=0=0 és f(4)=4=2.
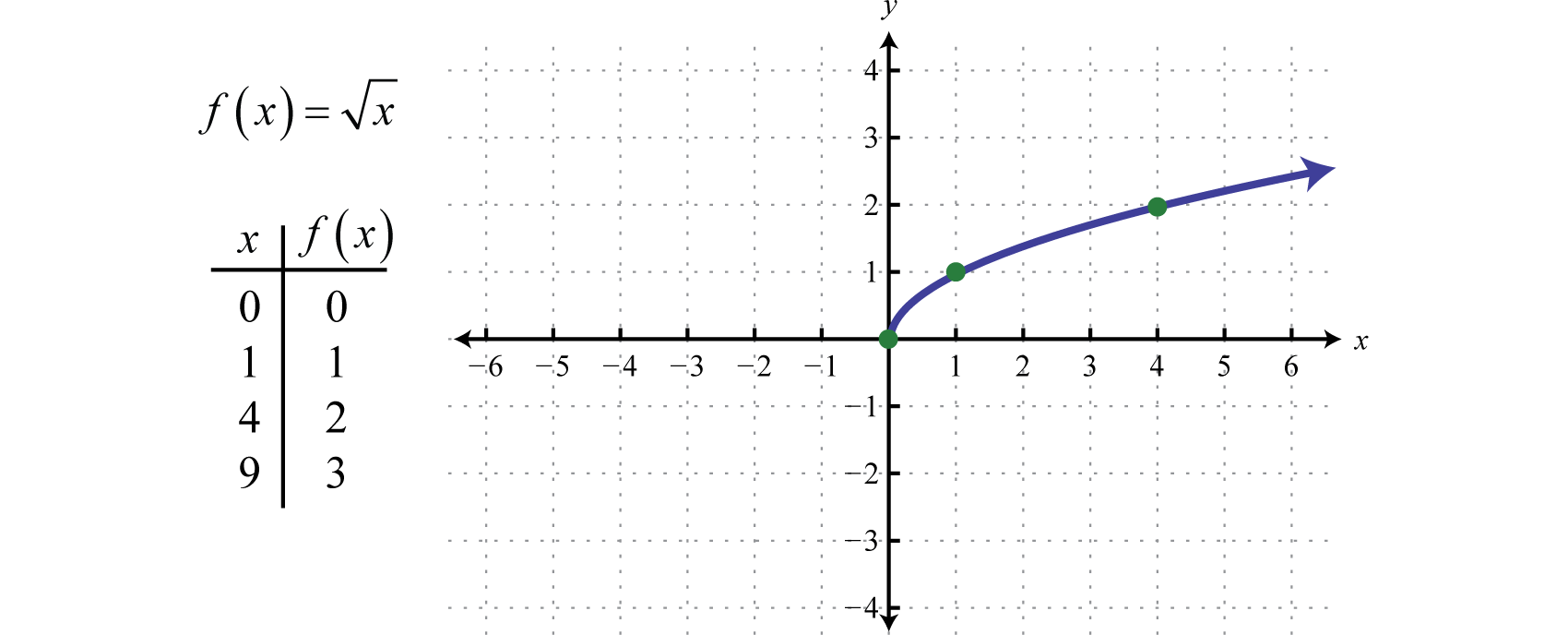
A tartomány és a tartomány egyaránt nullánál nagyobb vagy azzal egyenlő valós számokból áll [0,∞).
A reciprok függvényA f(x)=1x. által definiált f(x)=1x. által definiált függvény olyan racionális függvény, amelynek tartományára egy korlátozás van, nevezetesen x≠0. Egy nullához nagyon közeli x-érték reciprokja nagyon nagy. Például,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1,000)=1(11,000)=1⋅1,0001=1,000
Más szóval, ahogy az x-értékek a nullához közelednek, reciprokuk a pozitív vagy a negatív végtelen felé tendál. Ez egy függőleges aszimptotát ír leEgy függőleges vonal, amelyhez egy grafikon végtelenül közel kerül. az y tengelyen. Továbbá, ahol az x-értékek nagyon nagyok, ott a reciprok függvény eredménye nagyon kicsi.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11,000=0,001
Más szóval, ahogy az x-értékek nagyon nagyok lesznek, az eredő y-értékek a nulla felé tendálnak. Ez egy vízszintes aszimptotát ír leA vízszintes vonal, amelyhez egy grafikon végtelenül közel kerül, ahol az x-értékek ±∞ felé tendálnak. az x-tengelyen. Számos pont ábrázolása után meghatározható a reciprok függvény általános alakja.
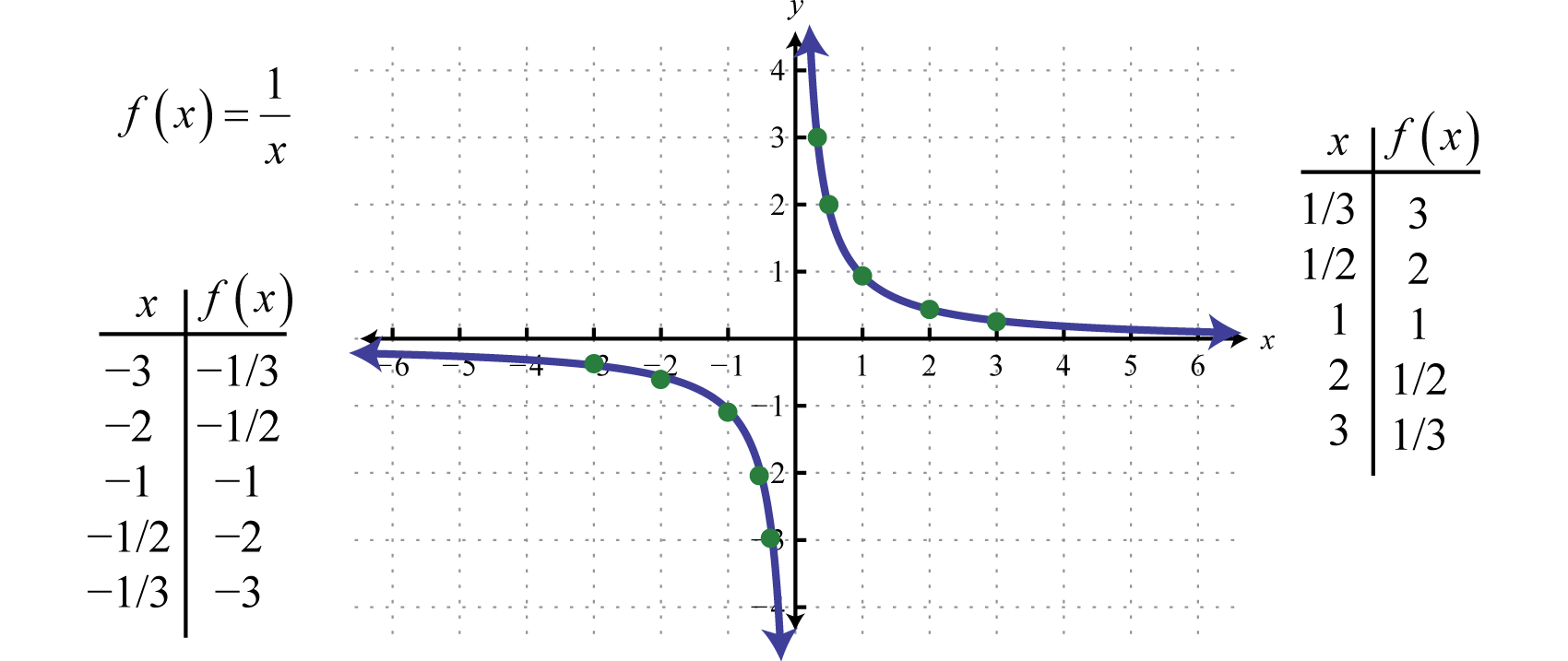
A reciprok függvény tartománya és tartománya is a 0 kivételével minden valós számból áll, ami intervallum jelöléssel a következőképpen fejezhető ki: (-∞,0)∪(0,∞).
