Perusfunktiot
Tässä jaksossa kuvaajaa seitsemän perusfunktiota, joita käytetään koko kurssin ajan. Kutakin funktiota grafisoidaan piirtämällä pisteitä. Muista, että f(x)=y ja siten f(x) ja y voidaan käyttää vaihdellen.
Jokaista funktiota, joka on muotoa f(x)=c, jossa c on mikä tahansa reaaliluku, kutsutaan vakiofunktioksiJokaista funktiota, joka on muotoa f(x)=c, jossa c on reaaliluku… Vakiofunktiot ovat lineaarisia ja ne voidaan kirjoittaa f(x)=0x+c. Tässä muodossa on selvää, että kaltevuus on 0 ja y-piste on (0,c). Arvioimalla mitä tahansa x:n arvoa, esimerkiksi x = 2, saadaan c.
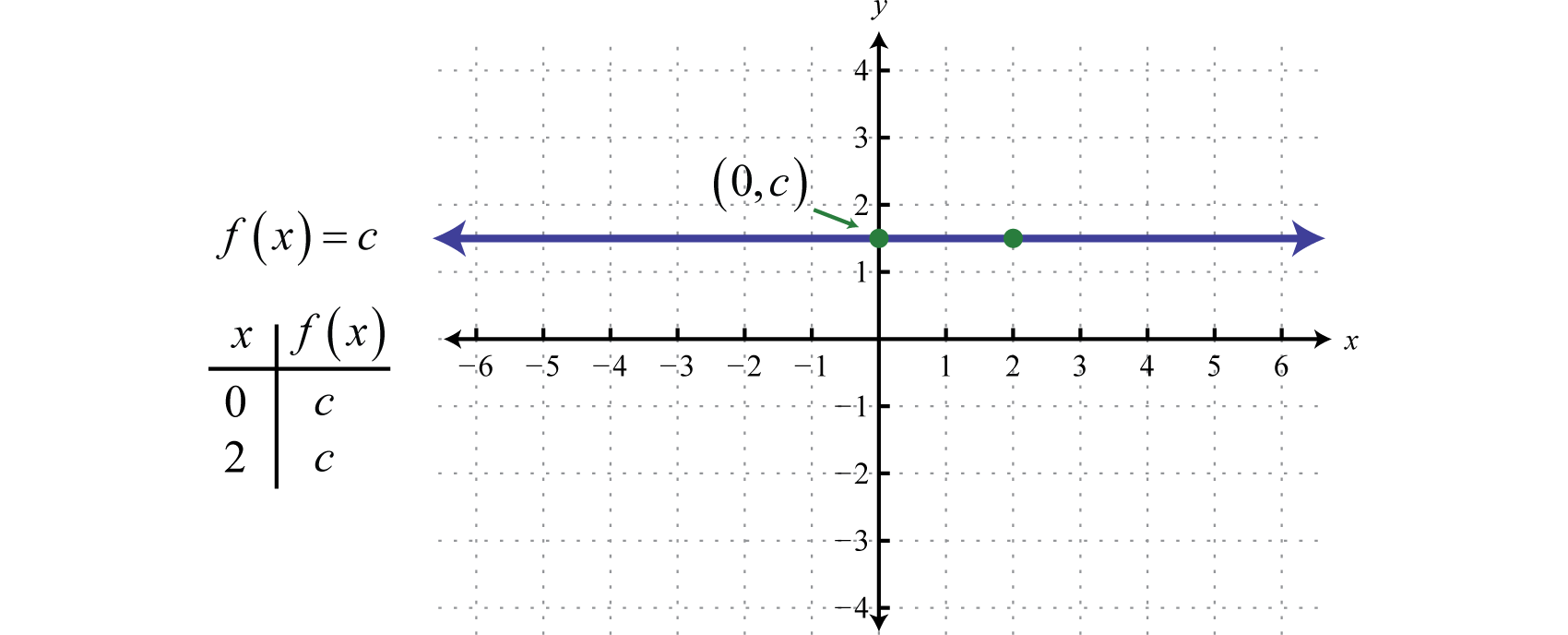
Vakiofunktion kuvaaja on vaakasuora viiva. Alue koostuu kaikista reaaliluvuista ℝ ja alue koostuu yhdestä ainoasta arvosta {c}.
Määrittelemme seuraavaksi identiteettifunktion Lineaarinen funktio, joka on määritelty seuraavasti: f(x)=x. f(x)=x. Arvioimalla mitä tahansa arvoa x:lle saadaan sama arvo. Esimerkiksi f(0)=0 ja f(2)=2. Identtifunktio on lineaarinen, f(x)=1x+0, jonka kaltevuus on m=1 ja y-piste (0, 0).
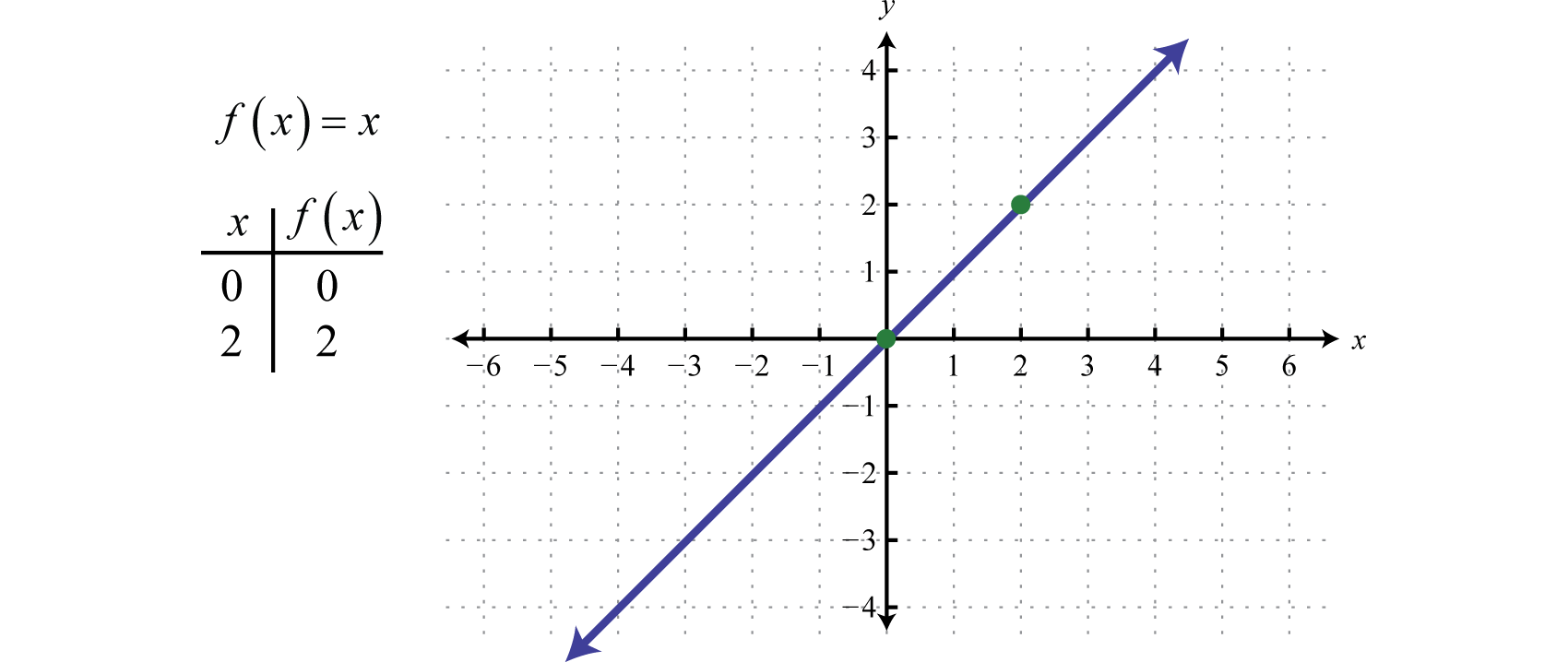
Alue ja alue koostuvat molemmat kaikista reaaliluvuista.
NeliöfunktioNeliöfunktio, joka on määritelty kaavalla f(x)=x2. f(x)=x2., joka on määritelty kaavalla f(x)=x2., on funktio, joka saadaan neliöimällä alueen arvot. Esimerkiksi f(2)=(2)2=4 ja f(-2)=(-2)2=4. Alueen nollasta poikkeavien arvojen neliöimisen tulos on aina positiivinen.
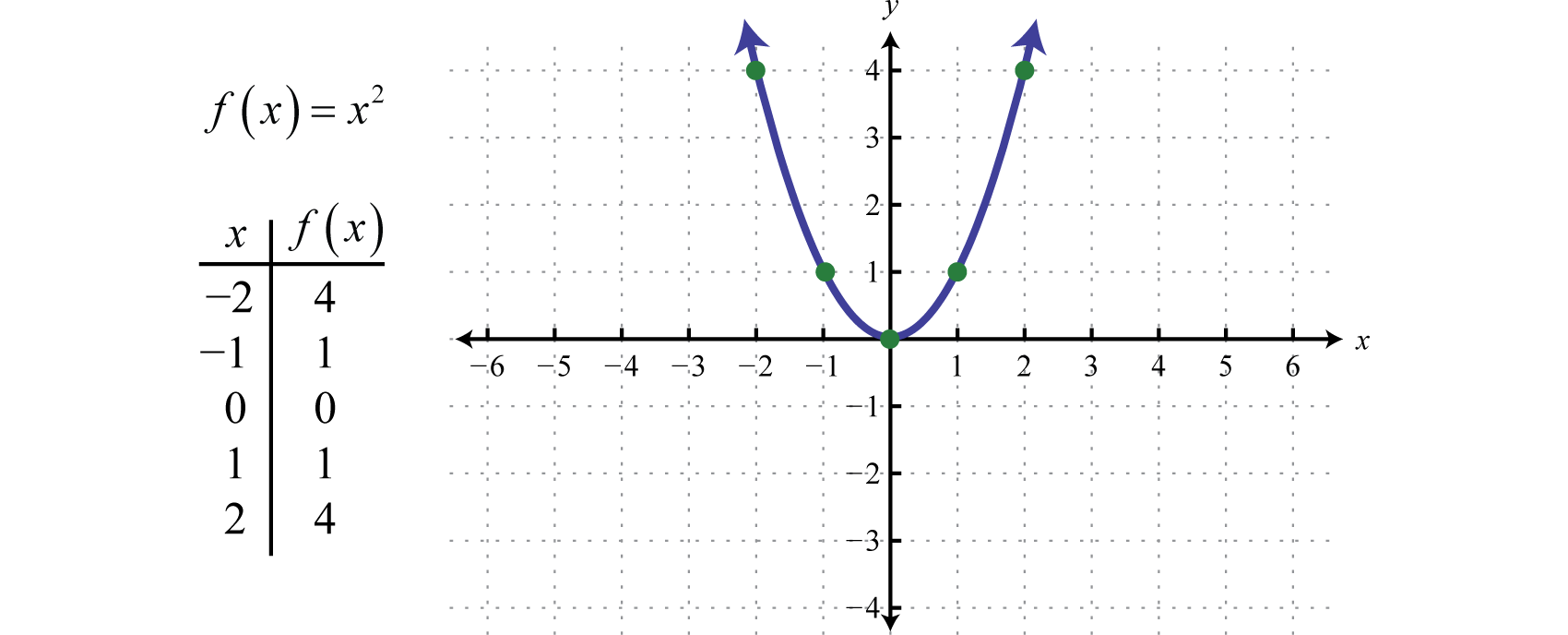
Tuloksena syntyvää kaarevaa kuvaajaa kutsutaan paraabeliksiNeliöfunktion muodostama kaareva kuvaaja… Alue koostuu kaikista reaaliluvuista ℝ ja alue koostuu kaikista y-arvoista, jotka ovat suurempia tai yhtä suuria kuin nolla [0,∞).
KuutiofunktioKuutiofunktio, joka määritellään kaavalla f(x)=x3., joka määritellään kaavalla f(x)=x3, korottaa kaikki alueen arvot kolmanteen potenssiin. Tulos voi olla joko positiivinen, nolla tai negatiivinen. Esimerkiksi f(1)=(1)3=1, f(0)=(0)3=0 ja f(-1)=(-1)3=-1.
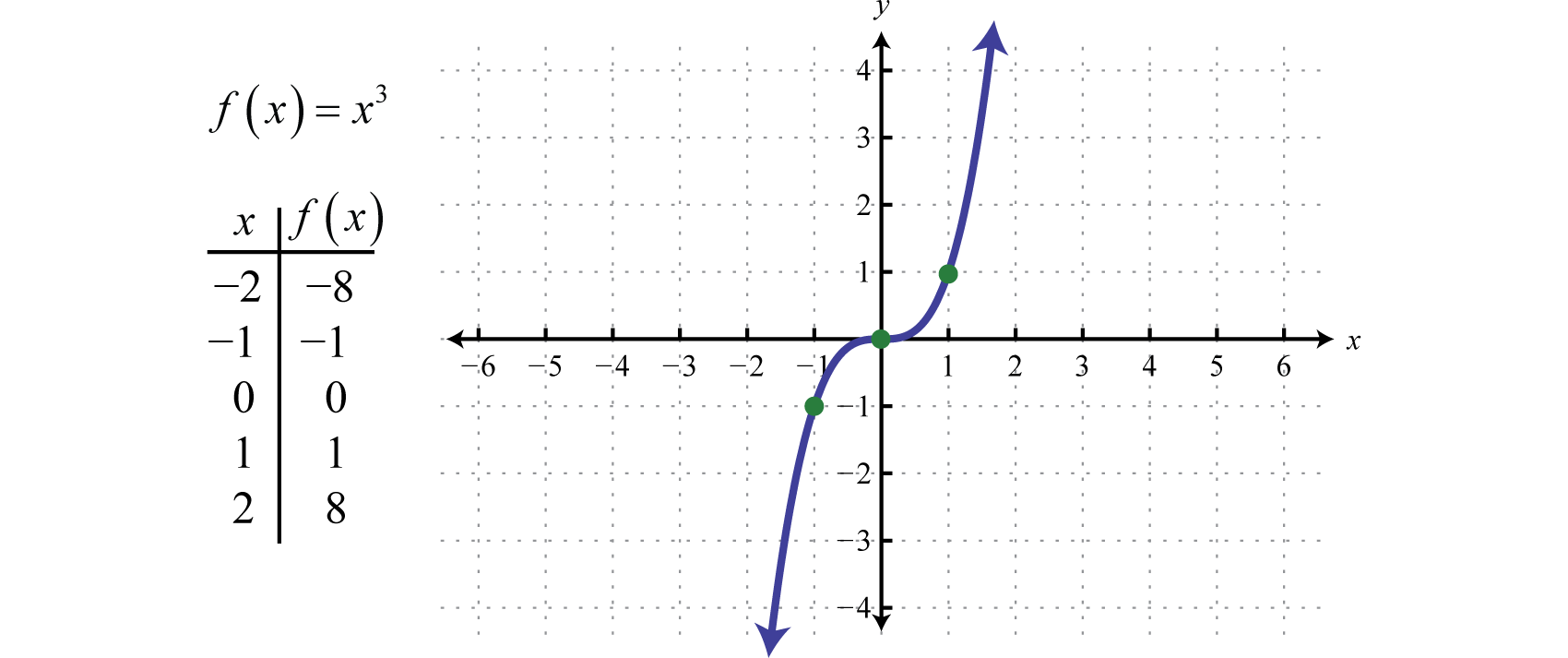
Alue ja alue koostuvat molemmat kaikista reaaliluvuista ℝ.
Huomaa, että vakio-, identiteetti-, neliö- ja kuutiofunktio ovat kaikki esimerkkejä peruspolynomifunktioista. Seuraavat kolme perusfunktiota eivät ole polynomeja.
AbsoluuttiarvofunktioFunktio, joka on määritelty f(x)=|x|., joka on määritelty f(x)=|x|, on funktio, jonka ulostulo edustaa etäisyyttä alkupisteeseen lukujonolla. Absoluuttisen arvon funktion arvioinnin tulos mille tahansa nollasta poikkeavalle x:n arvolle on aina positiivinen. Esimerkiksi f(-2)=|-2|=2 ja f(2)=|2|=2.
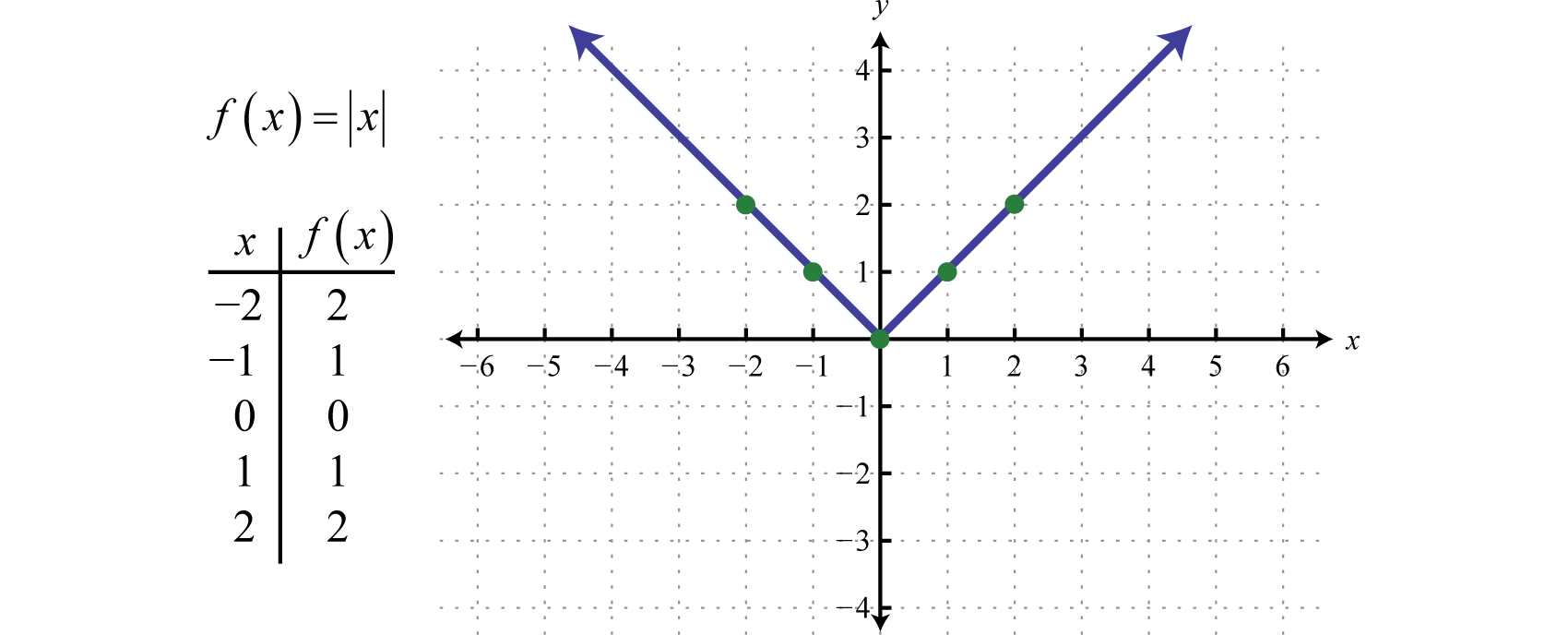
Absoluuttiarvofunktion alue koostuu kaikista reaaliluvuista ℝ ja alue kaikista y-arvoista, jotka ovat suurempia kuin nolla tai yhtä suuria kuin nolla [0,∞].
NeliöjuurifunktioFunktio, joka on määritelty seuraavalla funktiolla: f(x)=x .., määritelty f(x)=x, ei ole määritelty reaaliluvuksi, jos x-arvot ovat negatiivisia. Siksi pienin arvo toimialueella on nolla. Esimerkiksi f(0)=0=0 ja f(4)=4=2.
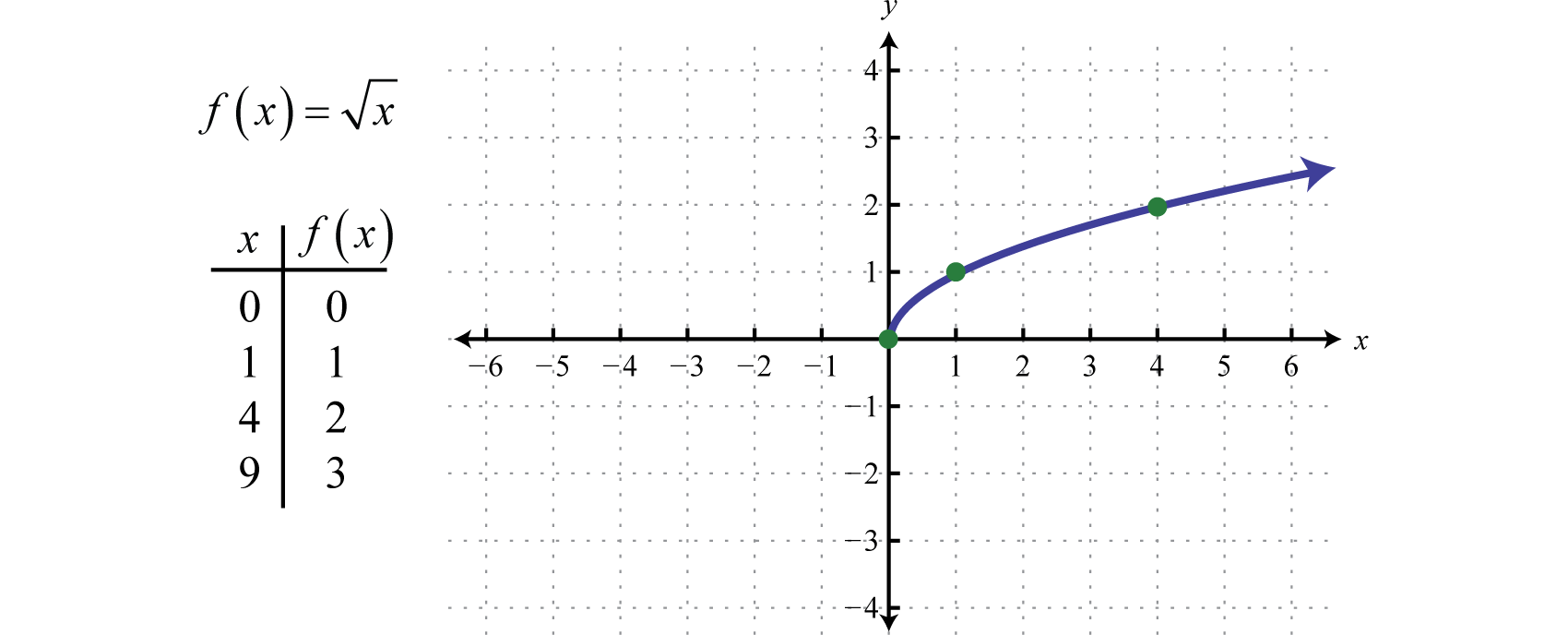
Alue ja alue koostuvat molemmat reaaliluvuista, jotka ovat suurempia kuin nolla tai yhtä suuria kuin nolla [0,∞).
RekvisiittofunktioFunktio, joka on määritelty f(x)=1x:llä., joka on määritetty f(x)=1x:llä, on rationaalifunktio, jolla on yksi toimialueeseen kohdistuva restriktio eli x≠0. Hyvin lähellä nollaa olevan x-arvon käänteisarvo on hyvin suuri. Esimerkiksi,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1,000)=1(11,000)=1⋅1,0001=1,000
Muilla sanoilla, x-arvojen lähestyessä nollaa niiden käänteisluvut pyrkivät joko positiiviseen tai negatiiviseen äärettömyyteen. Tämä kuvaa pystysuoraa asymptoottiaPystysuora viiva, jota kuvaaja tulee äärettömän lähelle. y-akselilla. Lisäksi, kun x-arvot ovat hyvin suuria, käänteisfunktion tulos on hyvin pieni.
f(10)=110=0.1f(100)=1100=0.01f(1000)=11,000=0.001
Muilla sanoilla, kun x-arvot kasvavat hyvin suuriksi, niiden tuloksena olevat y-arvot pyrkivät kohti nollaa. Tämä kuvaa vaakasuoraa asymptoottiaVaakasuora viiva, jota kuvaaja tulee äärettömän lähelle, kun x-arvot pyrkivät kohti ±∞. x-akselilla. Kun on piirretty useita pisteitä, voidaan määrittää vastavuoroisen funktion yleinen muoto.
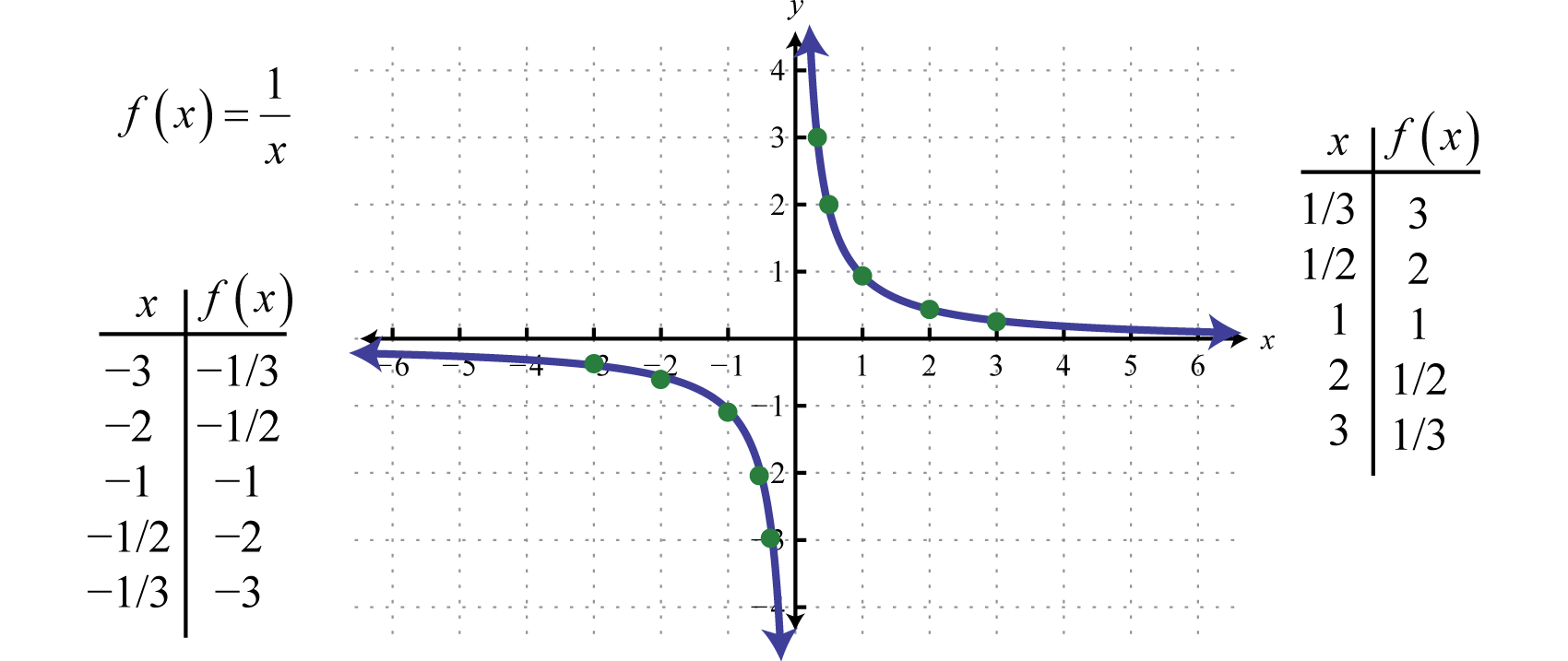
Vastavuoroisen funktion sekä alue että vaihteluväli koostuvat kaikista reaaliluvuista paitsi 0:sta, joka voidaan ilmaista intervallimerkinnällä seuraavasti: (-∞,0)∪(0,∞).
