Underfitting vs. Overfitting (vs. Best Fitting) beim maschinellen Lernen

Die Herausforderung von Underfitting und Overfitting beim maschinellen Lernen

Diese Frage wird Ihnen in einem Bewerbungsgespräch für einen Datenwissenschaftler unweigerlich gestellt:

Können Sie erklären, was Underfitting und Overfitting im Kontext des maschinellen Lernens sind?

Ihre Fähigkeit, dies auf nicht-technische und leicht verständliche Weise zu erklären, könnte darüber entscheiden, ob Sie für die Rolle des Datenwissenschaftlers geeignet sind!

Selbst wenn wir an einem Projekt zum maschinellen Lernen arbeiten, sind wir oft mit Situationen konfrontiert, in denen wir unerwartete Leistungs- oder Fehlerratenunterschiede zwischen der Trainingsmenge und der Testmenge feststellen (wie unten dargestellt). Wie kann es sein, dass ein Modell in der Trainingsmenge so gut abschneidet und in der Testmenge genauso schlecht?

Dies passiert sehr häufig, wenn ich mit baumbasierten Vorhersagemodellen arbeite. Aufgrund der Funktionsweise der Algorithmen können Sie sich vorstellen, wie schwierig es ist, nicht in die Overfitting-Falle zu tappen!

Außerdem kann es ziemlich entmutigend sein, wenn wir nicht in der Lage sind, den zugrundeliegenden Grund zu finden, warum unser Vorhersagemodell dieses anomale Verhalten zeigt.

Hier ist meine persönliche Erfahrung – fragen Sie einen erfahrenen Datenwissenschaftler nach diesem Thema, und er fängt in der Regel an, über eine Reihe ausgefallener Begriffe wie Overfitting, Underfitting, Bias und Varianz zu sprechen. Aber kaum jemand spricht über die Intuition hinter diesen Konzepten des maschinellen Lernens. Das wollen wir ändern, oder?

Lassen Sie uns ein Beispiel nehmen, um Underfitting vs. Overfitting zu verstehen

Ich möchte diese Konzepte anhand eines realen Beispiels erklären. Viele Leute reden über den theoretischen Blickwinkel, aber ich denke, das reicht nicht aus – wir müssen uns vergegenwärtigen, wie Underfitting und Overfitting tatsächlich funktionieren.

Zeigen wir uns also ein Beispiel aus unserer Studienzeit.

Betrachten wir eine Mathematikklasse, die aus drei Studenten und einem Professor besteht.

In jedem Klassenzimmer können wir die Studenten grob in drei Kategorien einteilen. Wir werden über sie einzeln sprechen.

Sagen wir, dass Student A einem Studenten ähnelt, der Mathe nicht mag. Sie interessiert sich nicht für das, was in der Klasse gelehrt wird, und schenkt daher dem Professor und dem Inhalt, den er lehrt, nicht viel Aufmerksamkeit.

Betrachten wir Student B. Er ist der wettbewerbsfähigste Student, der sich darauf konzentriert, jede einzelne Frage auswendig zu lernen, die in der Klasse gelehrt wird, anstatt sich auf die Schlüsselkonzepte zu konzentrieren. Im Grunde ist er nicht daran interessiert, den Problemlösungsansatz zu erlernen.

Schließlich haben wir die ideale Schülerin C. Sie ist ausschließlich daran interessiert, die Schlüsselkonzepte und den Problemlösungsansatz im Mathematikunterricht zu erlernen, anstatt nur die präsentierten Lösungen auswendig zu lernen.

Wir alle wissen aus Erfahrung, was in einem Klassenzimmer passiert. Der Professor hält zunächst eine Vorlesung und bringt den Schülern die Aufgaben und deren Lösung bei. Am Ende des Tages schreibt der Professor einfach ein Quiz, das auf dem basiert, was er in der Vorlesung gelehrt hat.

Das Hindernis kommt in den Semestertests3, die die Schule vorschreibt. Hier tauchen neue Fragen (ungesehene Daten) auf. Die Schüler haben diese Fragen noch nicht gesehen und schon gar nicht im Unterricht gelöst. Kommt Ihnen das bekannt vor?

Diskutieren wir also, was passiert, wenn der Lehrer am Ende des Tages eine Klassenarbeit schreibt:

• Schüler A, der in seiner eigenen Welt abgelenkt war, hat die Antworten einfach erraten und bekam in der Prüfung etwa 50 % der Punkte
• Der Schüler hingegen, der sich jede einzelne Frage aus dem Unterricht gemerkt hat, konnte fast alle Fragen auswendig beantworten und erhielt deshalb 98 % der Punkte in der Klassenarbeit
• Für Schüler C, löste sie tatsächlich alle Fragen mit dem Problemlösungsansatz, den sie im Unterricht gelernt hatte, und erzielte 92%

Wir können eindeutig ableiten, dass der Schüler, der einfach alles auswendig lernt, ohne große Schwierigkeiten bessere Ergebnisse erzielt.

Jetzt kommt der Knackpunkt. Schauen wir uns auch an, was während des monatlichen Tests passiert, wenn die Schüler mit neuen, unbekannten Fragen konfrontiert werden, die der Lehrer im Unterricht nicht gelehrt hat.

• Im Fall von Schüler A hat sich nicht viel geändert, und er beantwortet immer noch zufällig Fragen in ~50% der Fälle richtig.
• Im Fall von Schüler B ist seine Punktzahl deutlich gefallen. Können Sie sich denken, warum? Das liegt daran, dass er sich die Aufgaben, die im Unterricht gelehrt wurden, immer gemerkt hat, aber dieser monatliche Test enthielt Fragen, die er noch nie zuvor gesehen hat. Deshalb hat sich seine Leistung deutlich verschlechtert
• Bei Schülerin C ist die Punktzahl mehr oder weniger gleich geblieben. Das liegt daran, dass sie sich auf das Erlernen des Problemlösungsansatzes konzentrierte und daher in der Lage war, die gelernten Konzepte anzuwenden, um die unbekannten Fragen zu lösen

Wie hängt dies mit Underfitting und Overfitting beim maschinellen Lernen zusammen?

Sie fragen sich vielleicht, wie dieses Beispiel mit dem Problem zusammenhängt, das wir bei den Trainings- und Testergebnissen des Entscheidungsbaum-Klassifikators festgestellt haben? Gute Frage!

Lassen Sie uns also daran arbeiten, dieses Beispiel mit den Ergebnissen des Entscheidungsbaum-Klassifikators zu verbinden, den ich Ihnen zuvor gezeigt habe.

Zunächst ähneln die Klassenarbeit und der Klassentest den Trainingsdaten bzw. der Vorhersage über die Trainingsdaten selbst. Auf der anderen Seite repräsentiert der Semestertest die Testmenge aus unseren Daten, die wir beiseite legen, bevor wir unser Modell trainieren (oder ungesehene Daten in einem realen maschinellen Lernprojekt).

Erinnern Sie sich an unseren Entscheidungsbaum-Klassifikator, den ich bereits erwähnt habe. Er lieferte ein perfektes Ergebnis für den Trainingssatz, hatte aber Probleme mit dem Testsatz. Vergleicht man dies mit den soeben besprochenen Schülerbeispielen, so stellt der Klassifikator eine Analogie zu Schüler B her, der versuchte, sich jede einzelne Frage in der Trainingsmenge einzuprägen.

In ähnlicher Weise versucht unser Entscheidungsbaum-Klassifikator, jeden einzelnen Punkt aus den Trainingsdaten zu lernen, leidet aber radikal, wenn er auf einen neuen Datenpunkt in der Testmenge trifft. Er ist nicht in der Lage, sie gut zu verallgemeinern.

Diese Situation, in der ein bestimmtes Modell in den Trainingsdaten zu gut abschneidet, die Leistung aber in der Testmenge deutlich abnimmt, wird als Overfitting-Modell bezeichnet.

Zum Beispiel sind nichtparametrische Modelle wie Entscheidungsbäume, KNN und andere baumbasierte Algorithmen sehr anfällig für Overfitting. Diese Modelle können sehr komplexe Beziehungen erlernen, was zu einer Überanpassung führen kann. Das nachstehende Diagramm fasst dieses Konzept zusammen:

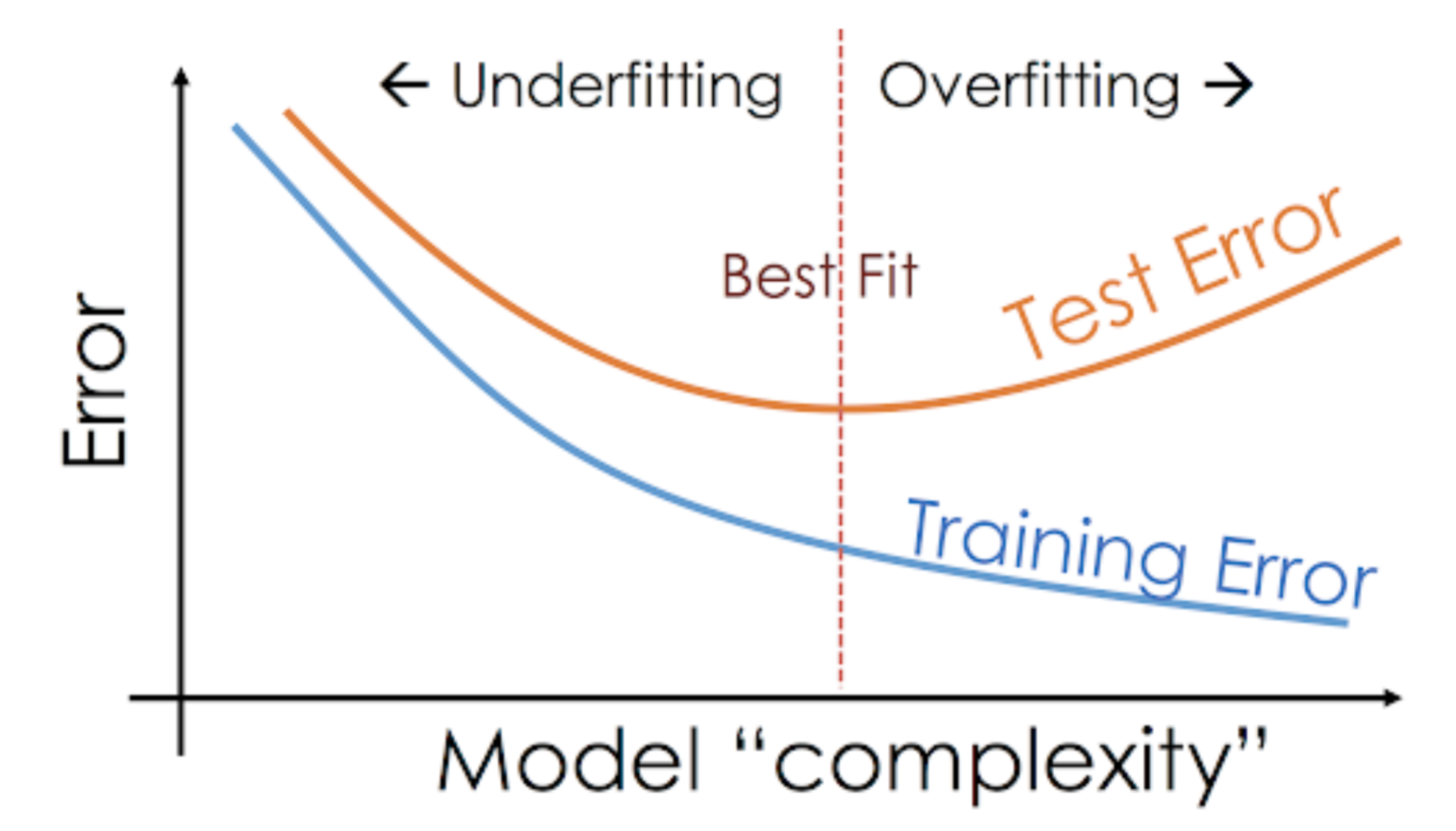
Wenn das Modell hingegen sowohl im Test- als auch im Trainingsset schlecht abschneidet, spricht man von einem Underfitting-Modell. Ein Beispiel für diese Situation wäre die Erstellung eines linearen Regressionsmodells über nicht lineare Daten.