Konstant acceleration
Analys av tvådimensionell projektilrörelse görs genom att dela upp den i två rörelser: längs den horisontella och vertikala axeln.
Lärandemål
Analysera en tvådimensionell projektilrörelse längs horisontella och vertikala axlar
Nyckelresultat
Nyckelpunkter
- Konstant acceleration i rörelse i två dimensioner följer i allmänhet ett projektilmönster.
- Projektilrörelse är rörelsen hos ett föremål som kastas eller projiceras upp i luften och som endast utsätts för den (vertikala) acceleration som beror på gravitationen.
- Vi analyserar tvådimensionell projektilrörelse genom att bryta upp den i två oberoende endimensionella rörelser längs den vertikala och horisontella axeln.
Nyckelbegrepp
- kinematisk: av eller relaterad till rörelse eller kinematik
Projektilrörelse är rörelsen hos ett föremål som kastas, eller projiceras, upp i luften, underkastat endast gravitationskraften. Föremålet kallas en projektil och dess väg kallas dess bana. Rörelsen hos fallande föremål är en enkel endimensionell typ av projektilrörelse där det inte finns någon horisontell rörelse. I en tvådimensionell projektilrörelse, t.ex. en fotboll eller ett annat kastat föremål, finns det både en vertikal och en horisontell komponent i rörelsen.
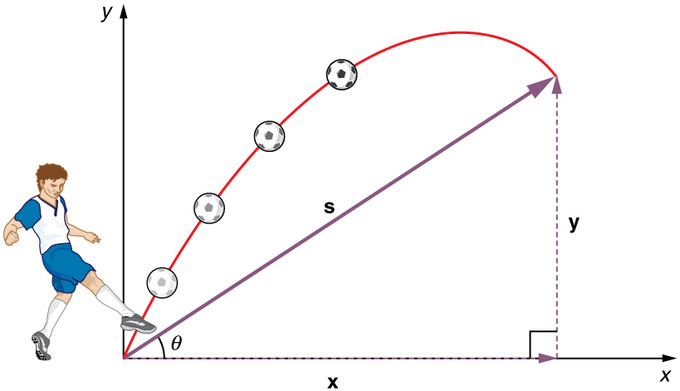
Projektilrörelse: Att kasta en sten eller sparka en boll ger i allmänhet ett projektilrörelsemönster som har både en vertikal och en horisontell komponent.
Det viktigaste att komma ihåg är att rörelser längs vinkelräta axlar är oberoende och kan därför analyseras separat. Nyckeln till att analysera tvådimensionell projektilrörelse är att dela upp den i två rörelser, en längs den horisontella axeln och en längs den vertikala. För att beskriva rörelsen måste vi hantera hastighet och acceleration samt förskjutning.
Vi kommer att anta att alla krafter utom gravitationen (såsom luftmotstånd och friktion, till exempel) är försumbara. Accelerationens komponenter är då mycket enkla: \text{a}_\text{y} = -\text{g} = -9,81 \frac{\text{m}}{\text{s}^2} (vi antar att rörelsen sker på tillräckligt små höjder nära jordytan så att accelerationen på grund av gravitationen är konstant). Eftersom gravitationsaccelerationen endast sker i vertikal riktning är \text{a}_\text{x} = 0. Därför kan de kinematiska ekvationer som beskriver rörelsen i \text{x}- respektive \text{y}-riktningen användas:
\text{x} = \text{x}_0 + \text{v}_\text{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
\text{v}_\text{y}^2=\text{v}_{0\text{y}}^2+2\text{a}_\text{y}(\text{y}-\text{y}_0)
Vi analyserar tvådimensionell projektilrörelse genom att bryta upp den i två oberoende endimensionella rörelser längs den vertikala och horisontella axeln. Den horisontella rörelsen är enkel, eftersom \text{a}_\text{x} = 0 och \text{v}_\text{x} därmed är konstant. Hastigheten i vertikal riktning börjar minska när ett föremål stiger; vid sin högsta punkt är den vertikala hastigheten noll. När ett föremål faller mot jorden igen ökar den vertikala hastigheten återigen i storlek men pekar i motsatt riktning mot den ursprungliga vertikala hastigheten. \text{x}- och \text{y}-rörelserna kan kombineras för att ge den totala hastigheten vid varje given punkt på banan.
