Funkcje podstawowe
W tym rozdziale wykreślimy siedem podstawowych funkcji, które będą używane w całym kursie. Każda funkcja jest przedstawiona na wykresie poprzez naniesienie punktów. Pamiętaj, że f(x)=y, a zatem f(x) i y mogą być używane zamiennie.
Każda funkcja postaci f(x)=c, gdzie c jest dowolną liczbą rzeczywistą, nazywana jest funkcją stałąKażda funkcja postaci f(x)=c, gdzie c jest liczbą rzeczywistą… Funkcje stałe są liniowe i można je zapisać w postaci f(x)=0x+c. W tej postaci jasne jest, że nachylenie wynosi 0, a punkt przecięcia y jest równy (0,c). Oceniając dowolną wartość x, np. x = 2, otrzymamy c.
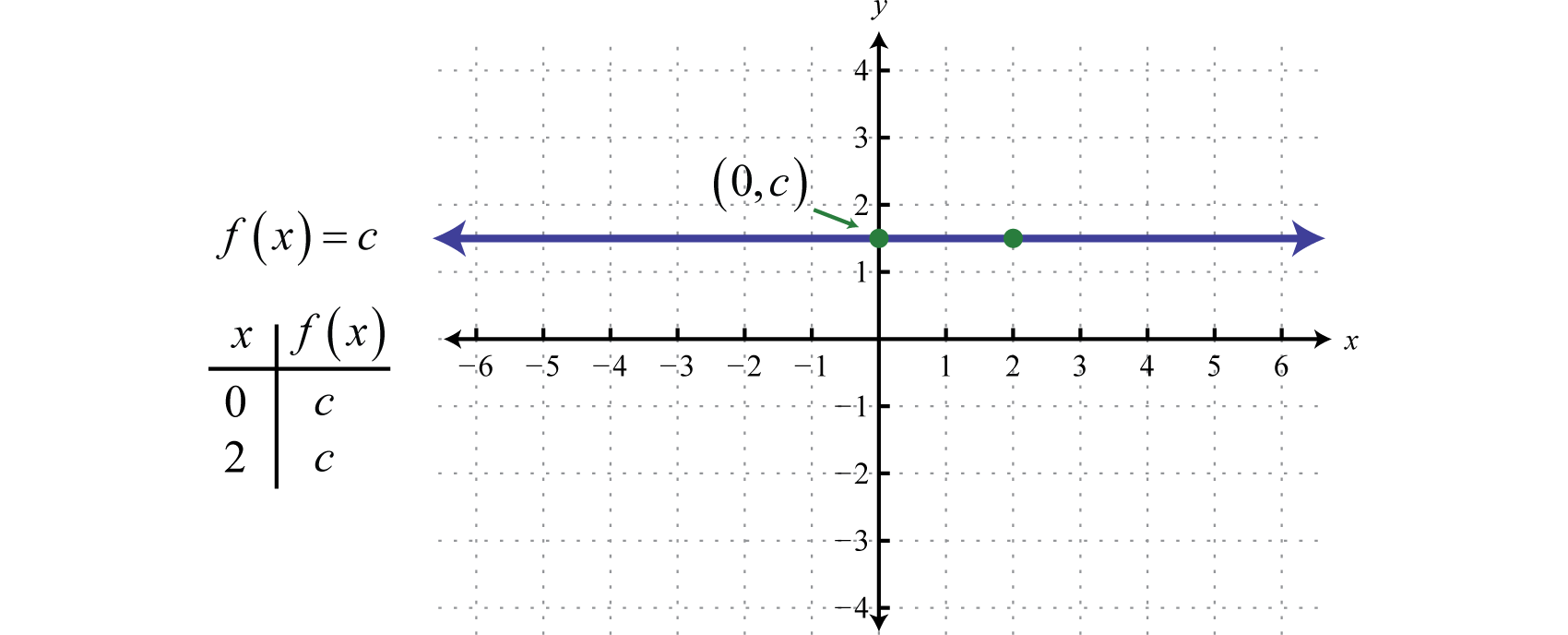
Wykresem funkcji stałej jest linia pozioma. Dziedziną są wszystkie liczby rzeczywiste ℝ, a przedziałem pojedyncza wartość {c}.
Następnie definiujemy funkcję tożsamościFunkcja liniowa określona przez f(x)=x. f(x)=x. Oceniając dowolną wartość dla x otrzymamy tę samą wartość. Na przykład, f(0)=0 i f(2)=2. Funkcja tożsamości jest liniowa, f(x)=1x+0, z nachyleniem m=1 i punktem przecięcia y (0, 0).
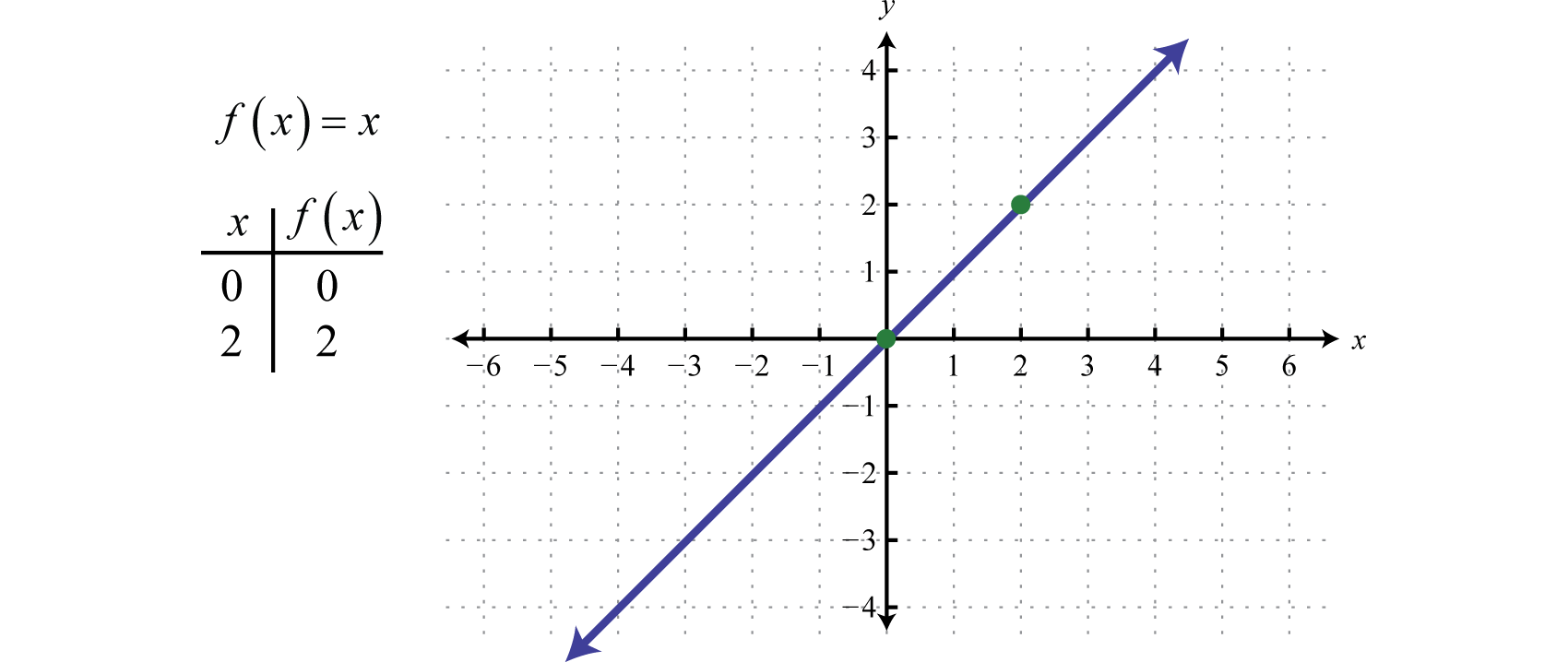
Działka i przedział składają się ze wszystkich liczb rzeczywistych.
Funkcja kwadratowaFunkcja kwadratowa określona przez f(x)=x2. określona przez f(x)=x2, jest funkcją otrzymaną przez podniesienie do kwadratu wartości w dziedzinie. Na przykład, f(2)=(2)2=4 oraz f(-2)=(-2)2=4. Wynik podniesienia do kwadratu niezerowych wartości w dziedzinie zawsze będzie dodatni.
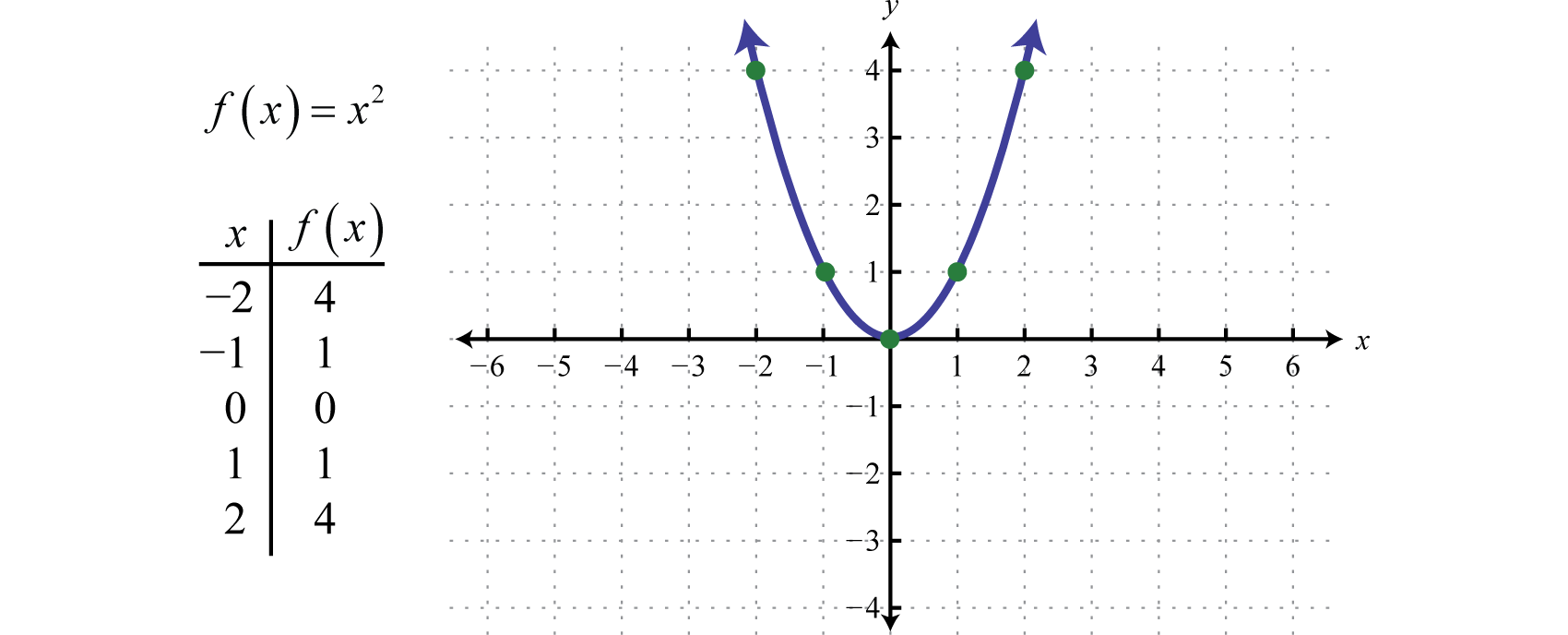
Otrzymany w ten sposób wykres krzywoliniowy nazywamy paraboląWykres krzywoliniowy utworzony przez funkcję kwadratową…. Dziedzina składa się ze wszystkich liczb rzeczywistych ℝ, a zakres ze wszystkich wartości y większych lub równych zero [0,∞].
Funkcja sześciennaFunkcja sześcienna zdefiniowana przez f(x)=x3. zdefiniowana przez f(x)=x3, podnosi wszystkie wartości w dziedzinie do trzeciej potęgi. Wyniki mogą być zarówno dodatnie, zerowe, jak i ujemne. Na przykład, f(1)=(1)3=1, f(0)=(0)3=0, a f(-1)=(-1)3=-1.
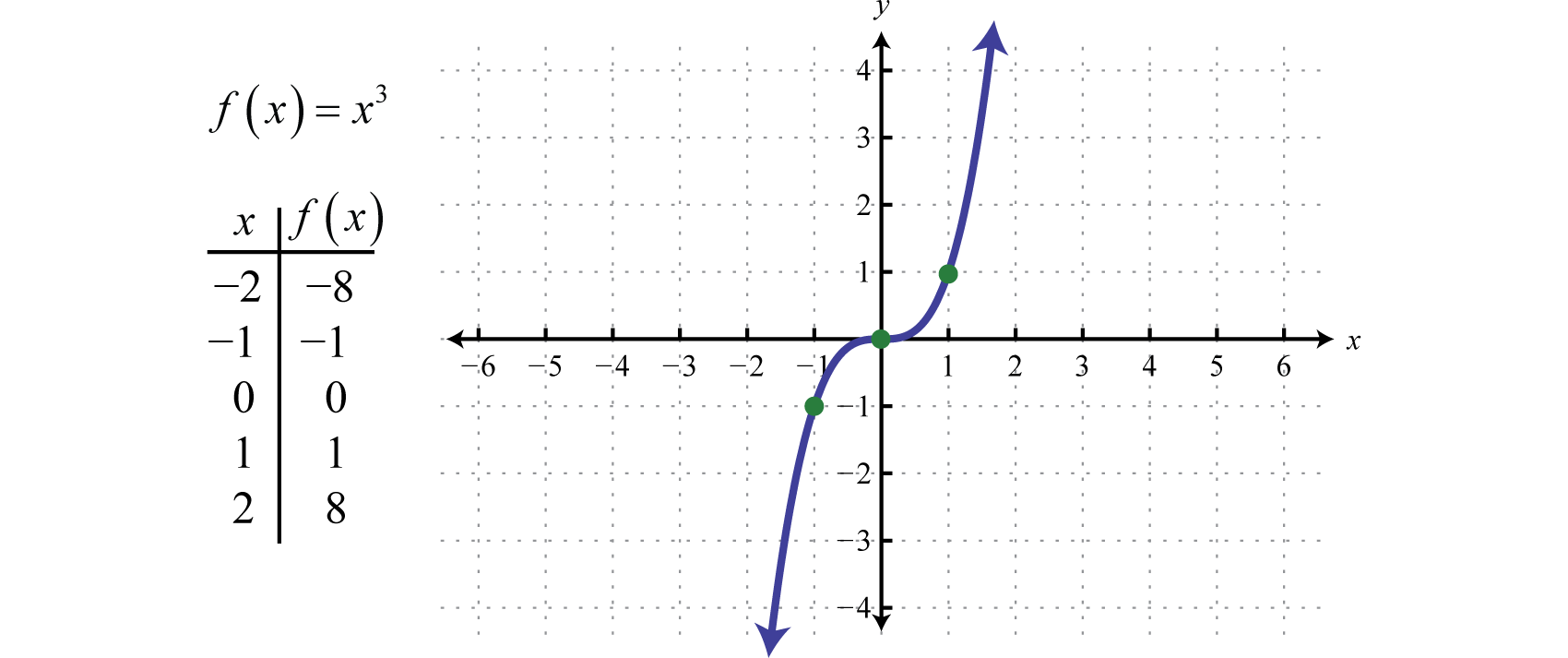
Działka i zakres składają się ze wszystkich liczb rzeczywistych ℝ.
Zauważ, że funkcja stała, funkcja tożsamości, funkcja kwadratowa i funkcja sześcienna są przykładami podstawowych funkcji wielomianowych. Kolejne trzy podstawowe funkcje nie są wielomianami.
Funkcja wartości bezwzględnejFunkcja określona przez f(x)=|x|., określona przez f(x)=|x|, jest funkcją, w której wynik przedstawia odległość do początku na linii liczbowej. Wynik obliczania funkcji wartości bezwzględnej dla dowolnej niezerowej wartości x będzie zawsze dodatni. Na przykład, f(-2)=|-2|=2 i f(2)=|2|=2.
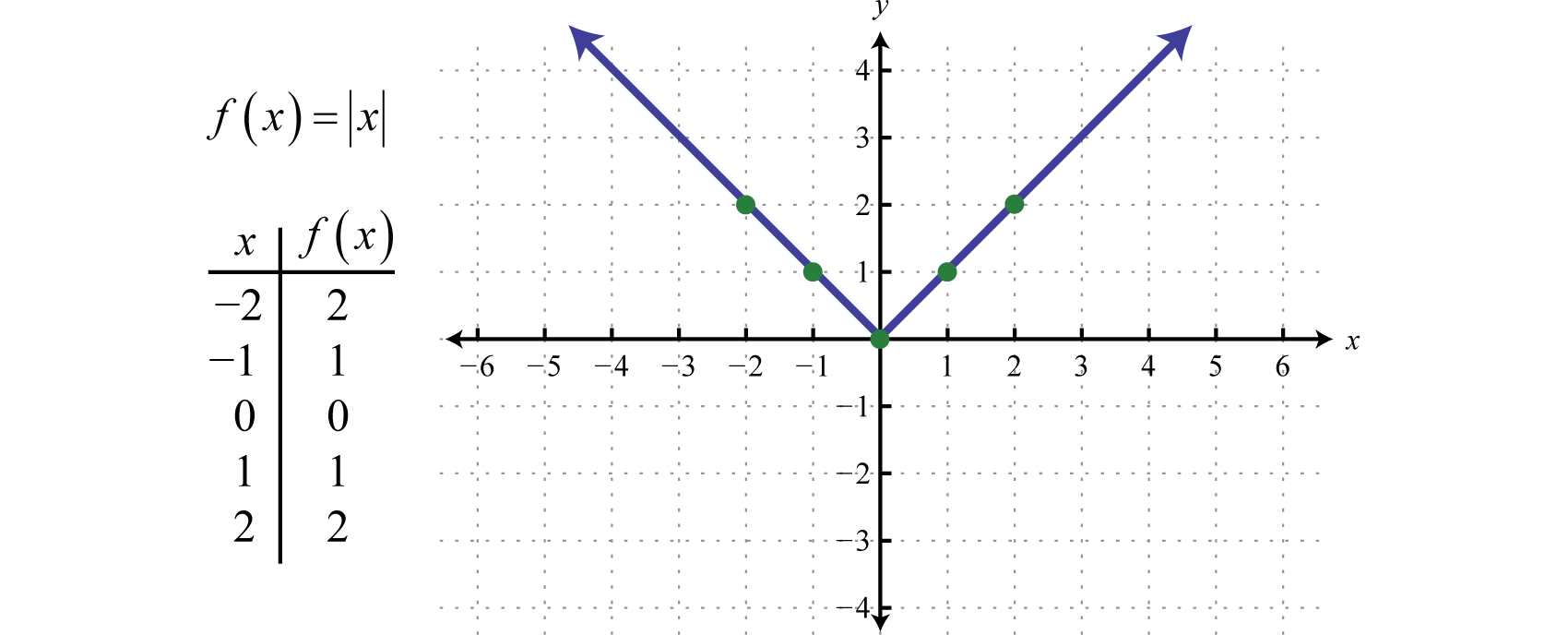
Dziedzina funkcji wartości bezwzględnej składa się ze wszystkich liczb rzeczywistych ℝ, a przedział składa się ze wszystkich wartości y większych lub równych zero [0,∞).
Funkcja pierwiastka kwadratowegoFunkcja zdefiniowana przez f(x)=x.., zdefiniowana przez f(x)=x, nie jest zdefiniowana jako liczba rzeczywista, jeśli wartości x są ujemne. Dlatego najmniejszą wartością w dziedzinie jest zero. Na przykład, f(0)=0=0 i f(4)=4=2.
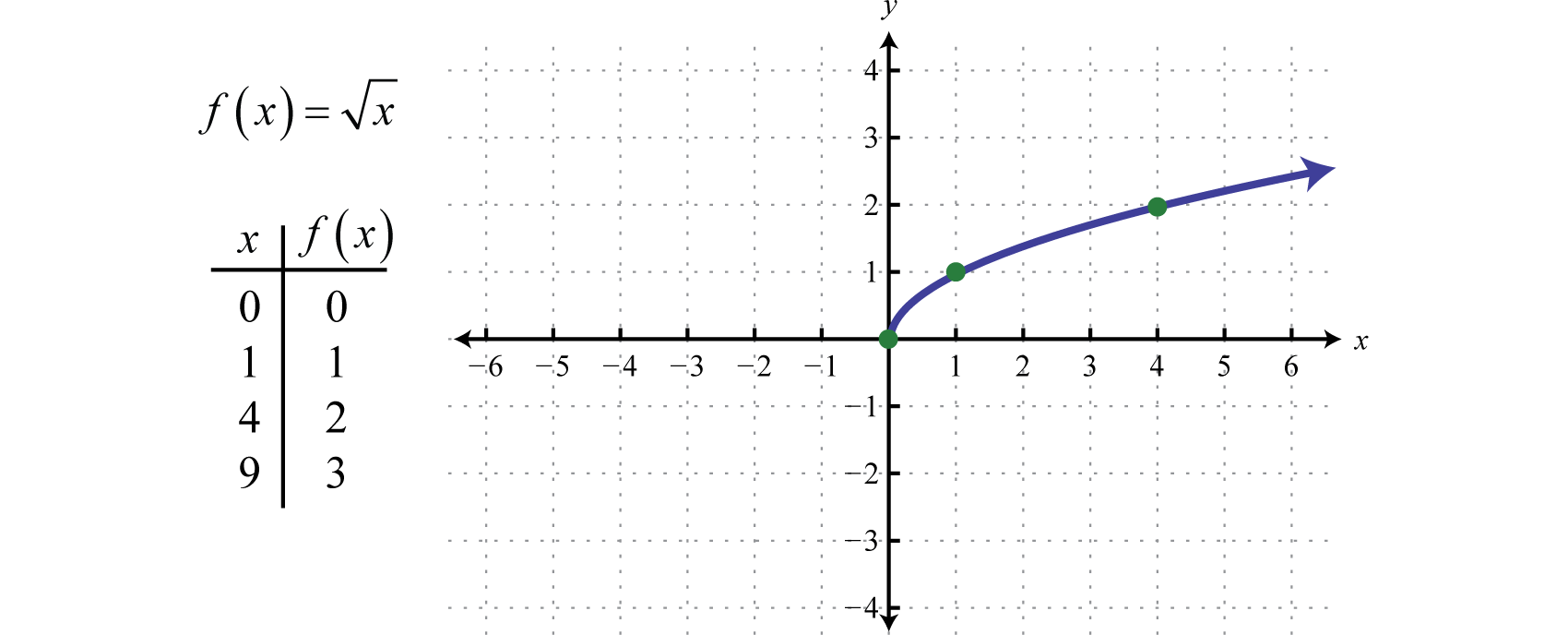
Działka i przedział składają się z liczb rzeczywistych większych lub równych zero [0,∞).
Funkcja odwrotnościFunkcja określona przez f(x)=1x., zdefiniowana przez f(x)=1x, jest funkcją racjonalną z jednym ograniczeniem na dziedzinę, mianowicie x≠0. Odwrotność wartości x bardzo bliskiej zeru jest bardzo duża. Na przykład,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1,000)=1(11,000)=1⋅1,0001=1,000
Innymi słowy, w miarę zbliżania się wartości x do zera ich odwrotności będą dążyły do dodatniej lub ujemnej nieskończoności. Opisuje to pionową asymptotęPionowa linia, do której wykres zbliża się nieskończenie blisko. na osi y. Ponadto, gdy wartości x są bardzo duże, wynik funkcji odwrotności jest bardzo mały.
f(10)=110=0.1f(100)=1100=0.01f(1000)=11,000=0.001
Innymi słowy, gdy wartości x stają się bardzo duże, wynikowe wartości y dążą do zera. Opisuje to asymptotę poziomąPozioma linia, do której wykres zbliża się w nieskończoność, gdy wartości x mają tendencję do ±∞. na osi x. Po wykreśleniu pewnej liczby punktów można określić ogólny kształt funkcji odwrotności.
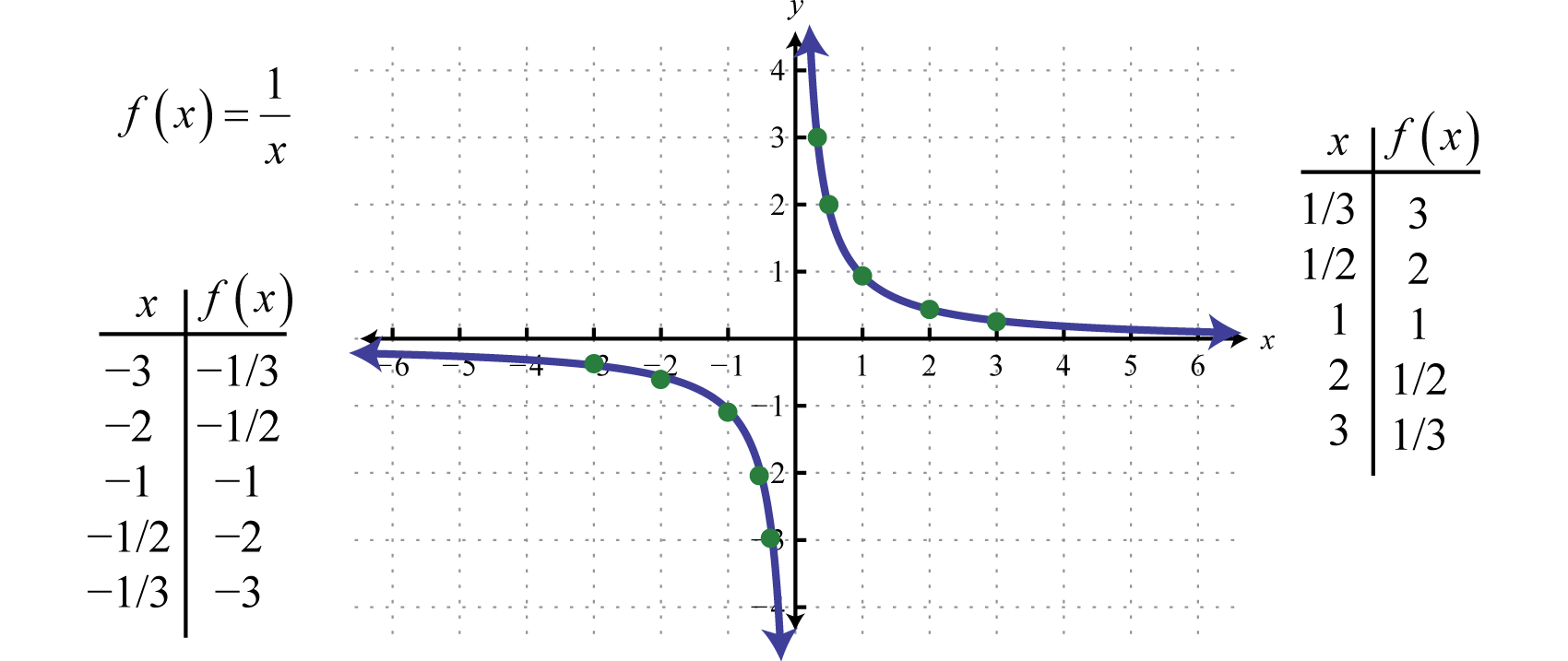
Zarówno dziedzina, jak i zakres funkcji odwrotności składa się ze wszystkich liczb rzeczywistych z wyjątkiem 0, co można wyrazić za pomocą notacji przedziałowej w następujący sposób: (-∞,0)∪(0,∞).
