Funzioni di base
In questa sezione grafichiamo sette funzioni di base che verranno utilizzate durante il corso. Ogni funzione viene rappresentata graficamente tracciando dei punti. Ricordate che f(x)=y e quindi f(x) e y possono essere usati in modo intercambiabile.
Ogni funzione della forma f(x)=c, dove c è un numero reale qualsiasi, è chiamata funzione costanteOgni funzione della forma f(x)=c dove c è un numero reale. Le funzioni costanti sono lineari e possono essere scritte f(x)=0x+c. In questa forma, è chiaro che la pendenza è 0 e l’intercetta y è (0,c). Valutando qualsiasi valore di x, come x = 2, si otterrà c.
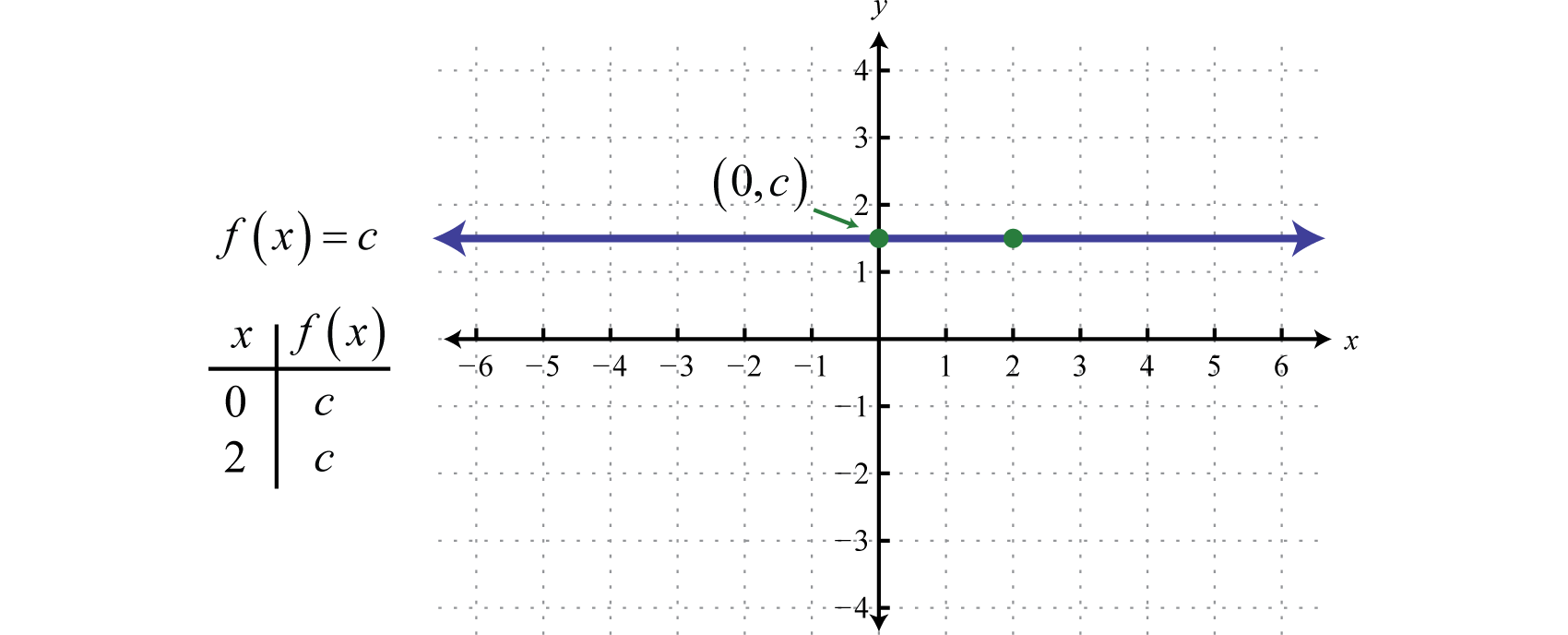
Il grafico di una funzione costante è una linea orizzontale. Il dominio è costituito da tutti i numeri reali ℝ e l’intervallo è costituito dal singolo valore {c}.
Definiremo poi la funzione identitàLa funzione lineare definita da f(x)=x. f(x)=x. Valutando qualsiasi valore per x si otterrà lo stesso valore. Per esempio, f(0)=0 e f(2)=2. La funzione identità è lineare, f(x)=1x+0, con pendenza m=1 e intercetta y (0, 0).
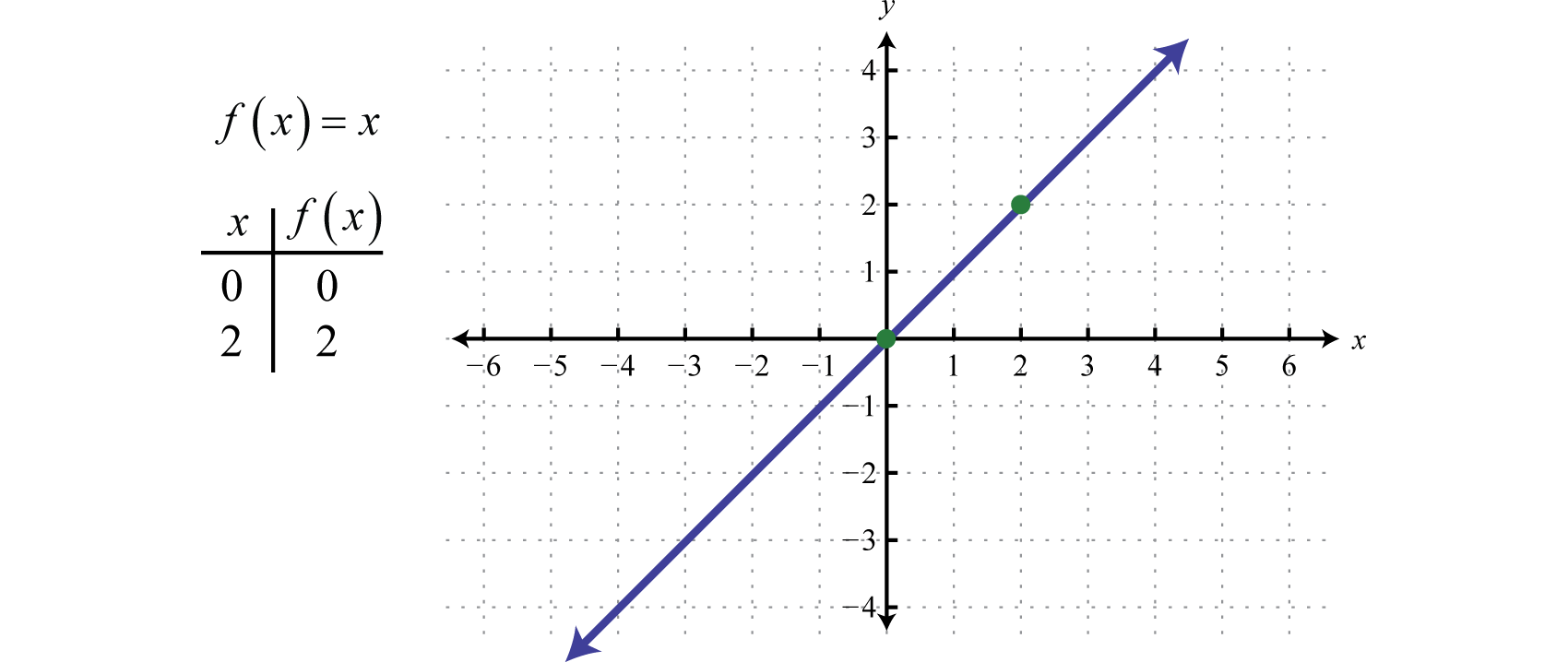
Il dominio e l’intervallo consistono entrambi di tutti i numeri reali.
La funzione quadraticaLa funzione quadratica definita da f(x)=x2., definita da f(x)=x2, è la funzione ottenuta squadrando i valori nel dominio. Per esempio, f(2)=(2)2=4 e f(-2)=(-2)2=4. Il risultato della quadratura dei valori non nulli nel dominio sarà sempre positivo.
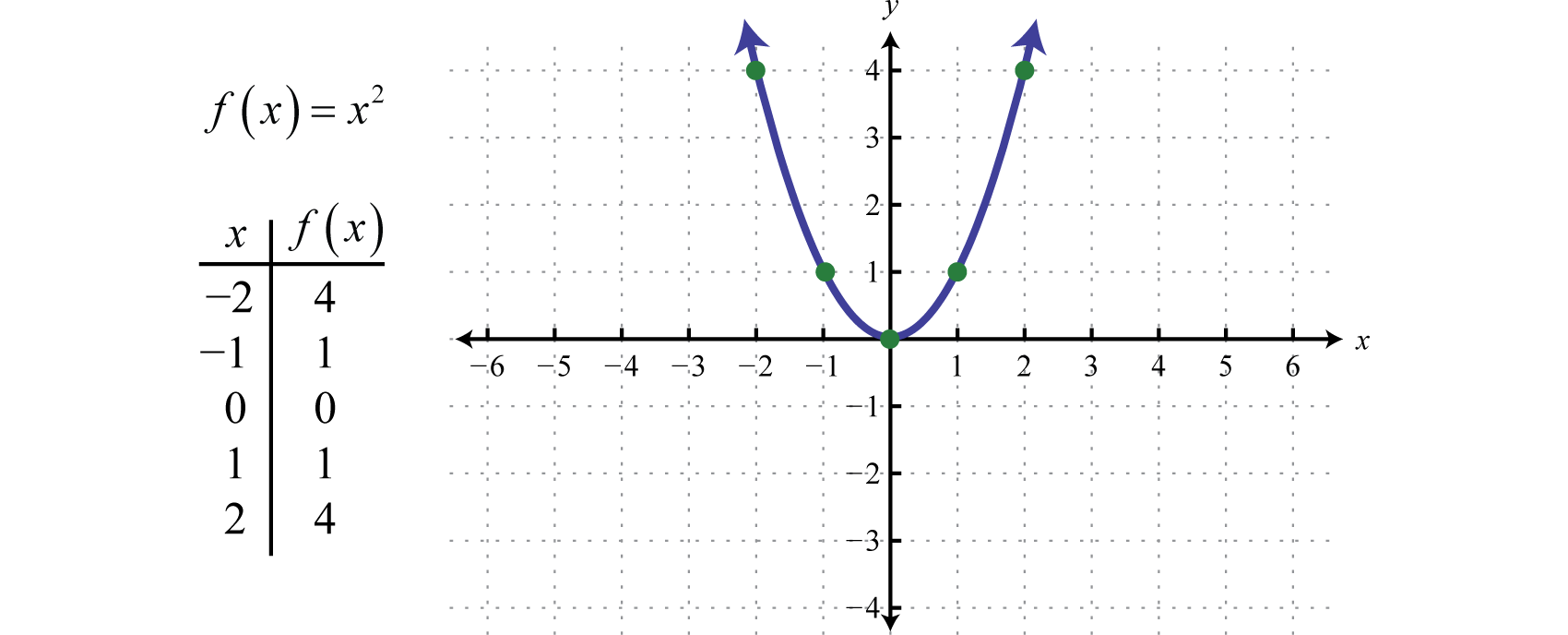
Il grafico curvo risultante è chiamato parabolaIl grafico curvo formato dalla funzione di quadratura. Il dominio è costituito da tutti i numeri reali ℝ e l’intervallo è costituito da tutti i valori di y maggiori o uguali a zero [0,∞).
La funzione cubicaLa funzione cubica definita da f(x)=x3., definita da f(x)=x3, eleva tutti i valori nel dominio alla terza potenza. I risultati possono essere positivi, zero o negativi. Per esempio, f(1)=(1)3=1, f(0)=(0)3=0, e f(-1)=(-1)3=-1.
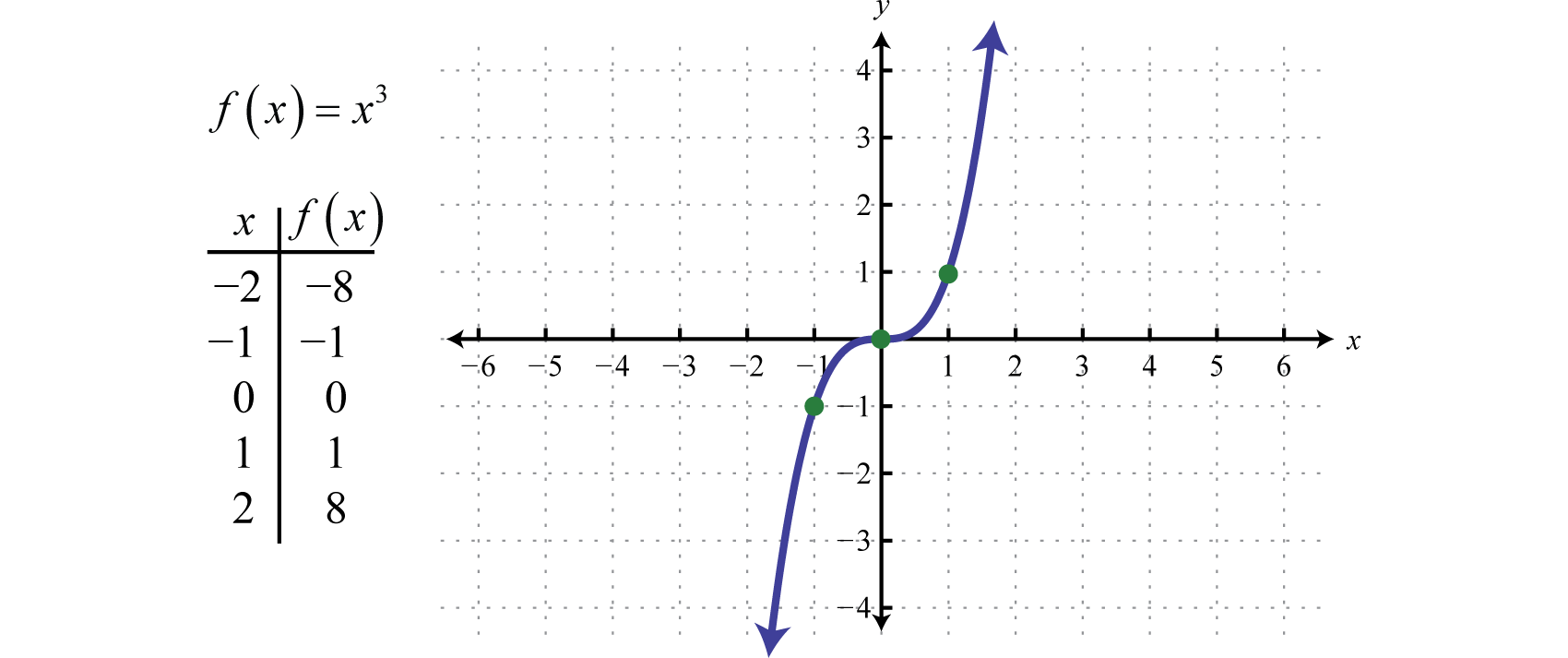
Il dominio e l’intervallo consistono entrambi in tutti i numeri reali ℝ.
Nota che le funzioni costante, identità, quadratura e cubatura sono tutti esempi di funzioni polinomiali di base. Le prossime tre funzioni di base non sono polinomi.
La funzione valore assolutoLa funzione definita da f(x)=|x|., definita da f(x)=|x|, è una funzione dove l’uscita rappresenta la distanza dall’origine su una linea numerica. Il risultato della valutazione della funzione valore assoluto per qualsiasi valore non nullo di x sarà sempre positivo. Per esempio, f(-2)=|-2|=2 e f(2)=|2|=2.
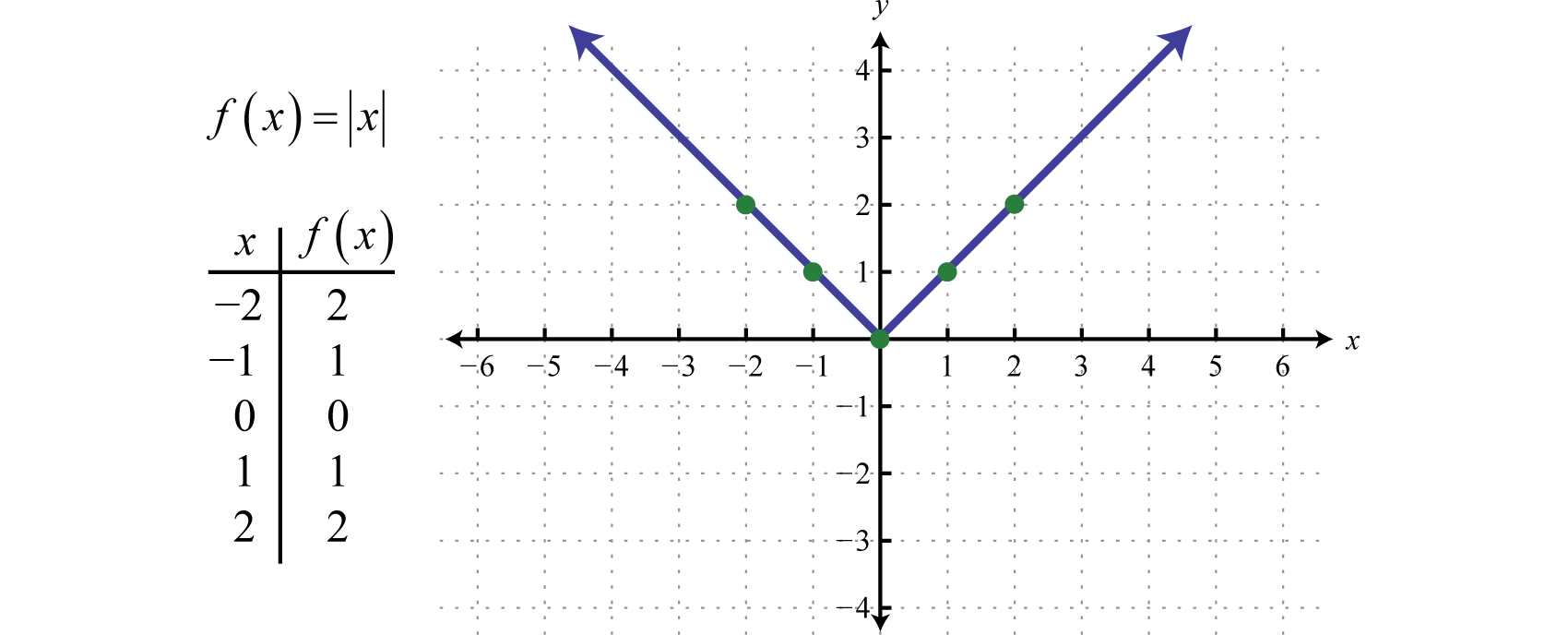
Il dominio della funzione valore assoluto consiste in tutti i numeri reali ℝ e l’intervallo consiste in tutti i valori di y maggiori o uguali a zero [0,∞).
La funzione radice quadrataLa funzione definita da f(x)=x, definita da f(x)=x, non è definita come un numero reale se i valori di x sono negativi. Pertanto, il valore più piccolo nel dominio è zero. Per esempio, f(0)=0=0 e f(4)=4=2.
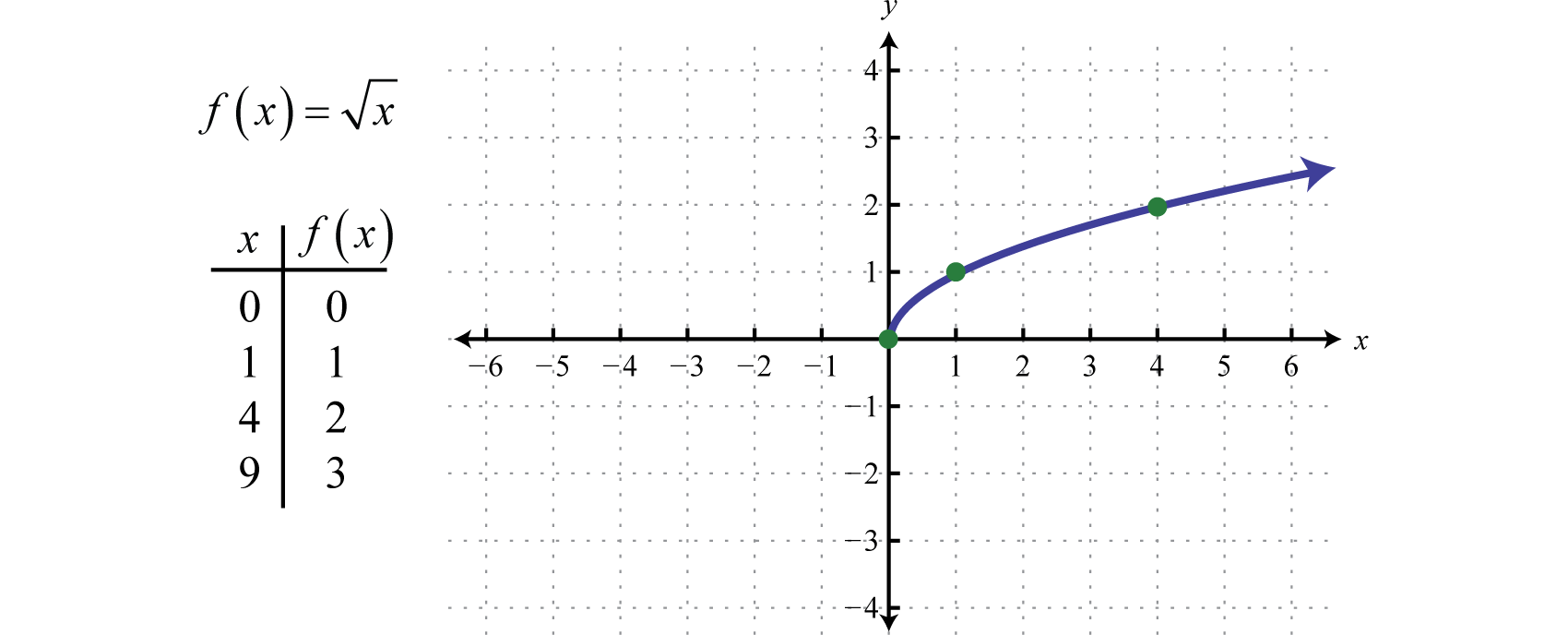
Il dominio e l’intervallo consistono entrambi di numeri reali maggiori o uguali a zero [0,∞).
La funzione reciprocaLa funzione definita da f(x)=1x., definita da f(x)=1x, è una funzione razionale con una restrizione sul dominio, cioè x≠0. Il reciproco di un valore di x molto vicino a zero è molto grande. Per esempio,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1.000)=1(11.000)=1⋅1.0001=1.000
In altre parole, come i valori di x si avvicinano allo zero i loro reciproci tenderanno verso l’infinito positivo o negativo. Questo descrive un asintoto verticaleUna linea verticale a cui un grafico diventa infinitamente vicino. all’asse y. Inoltre, dove i valori x sono molto grandi, il risultato della funzione reciproca è molto piccolo.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11.000=0,001
In altre parole, quando i valori x diventano molto grandi, i valori y risultanti tendono a zero. Questo descrive un asintoto orizzontaleUna linea orizzontale a cui un grafico diventa infinitamente vicino dove i valori x tendono a ±∞. all’asse x. Dopo aver tracciato un certo numero di punti si può determinare la forma generale della funzione reciproca.
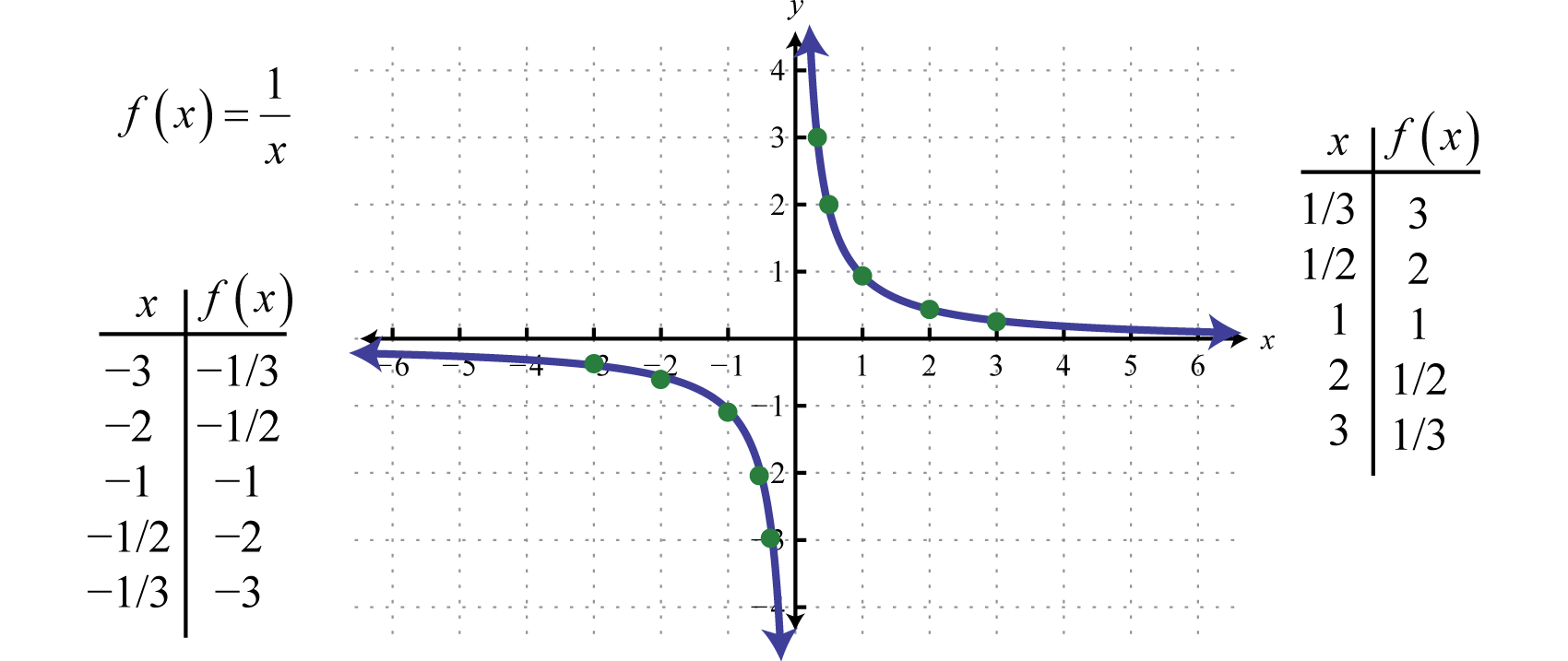
Sia il dominio che l’intervallo della funzione reciproca consistono di tutti i numeri reali tranne 0, che può essere espresso usando la notazione di intervallo come segue: (-∞,0)∪(0,∞).
