Acesso Constante
O movimento do projéctil bidimensional é feito dividindo-o em dois movimentos: ao longo dos eixos horizontal e vertical.
Objectivos de aprendizagem
Analisar um movimento bidimensional do projéctil ao longo dos eixos horizontal e vertical
Requisitos de aprendizagem
Pontos-chave
- A aceleração constante em movimento em duas dimensões segue geralmente um padrão de projéctil.
- Movimento projéctil é o movimento de um objecto lançado ou projectado no ar, sujeito apenas à aceleração (vertical) devido à gravidade.
- Analisamos o movimento bidimensional do projéctil, quebrando-o em dois movimentos unidimensionais independentes ao longo dos eixos vertical e horizontal.
Termos chave
- cinemática: do ou relativo ao movimento ou cinemática
Movimento projéctil é o movimento de um objecto lançado, ou projectado, no ar, sujeito apenas à força da gravidade. O objeto é chamado de projétil, e seu caminho é chamado de trajetória. O movimento dos objetos em queda é um tipo simples de movimento unidimensional do projétil, no qual não há movimento horizontal. No movimento bidimensional do projéctil, tal como o de uma bola de futebol ou outro objecto atirado, há uma componente vertical e uma componente horizontal ao movimento.
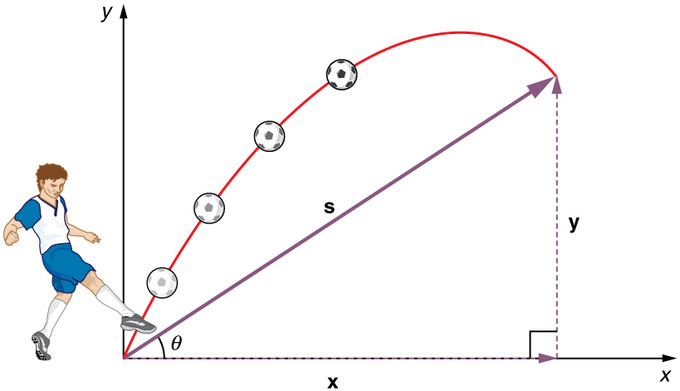
Projectile Motion: Lançar uma pedra ou chutar uma bola geralmente produz um padrão de movimento do projétil que tem um componente vertical e um horizontal.
O fato mais importante a lembrar é que o movimento ao longo dos eixos perpendiculares é independente e, portanto, pode ser analisado separadamente. A chave para analisar o movimento bidimensional do projétil é quebrá-lo em dois movimentos, um ao longo do eixo horizontal e o outro ao longo da vertical. Para descrever o movimento devemos lidar com velocidade e aceleração, bem como com deslocamento.
Assumiremos que todas as forças exceto a gravidade (como a resistência ao ar e o atrito, por exemplo) são insignificantes. Os componentes da aceleração são então muito simples: \texto{a}_texto{y} = -texto{g} = -9,81 {m} ^2} (assumimos que o movimento ocorre em alturas suficientemente pequenas perto da superfície da terra para que a aceleração devida à gravidade seja constante). Como a aceleração devida à gravidade é apenas na direção vertical, {a}_texto{x} = 0. Assim, as equações cinemáticas que descrevem o movimento ao longo das direções {x} e {y} respectivamente, podem ser usadas:
\i>texto{x} = \i>texto{x}_0 + \i>texto{v}_texto{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} O movimento horizontal é simples, porque \text{a}_texto{x} = 0 e \text{v}_texto{x} é assim constante. A velocidade no sentido vertical começa a diminuir à medida que um objeto sobe; no seu ponto mais alto, a velocidade vertical é zero. Quando um objecto cai novamente em direcção à Terra, a velocidade vertical aumenta de novo em magnitude mas aponta no sentido oposto ao da velocidade vertical inicial. Os movimentos \texto{x} e \texto{y} podem ser recombinados para dar a velocidade total em qualquer ponto dado da trajectória.
