Basisfuncties
In dit deel wordt een grafiek gemaakt van zeven basisfuncties die in deze cursus zullen worden gebruikt. Elke functie wordt grafisch weergegeven door punten te plotten. Onthoud dat f(x)=y en dus kunnen f(x) en y door elkaar worden gebruikt.
Een functie van de vorm f(x)=c, waarbij c een reëel getal is, wordt een constante functie genoemdEen functie van de vorm f(x)=c, waarbij c een reëel getal is… Constante functies zijn lineair en kunnen geschreven worden als f(x)=0x+c. In deze vorm is het duidelijk dat de helling 0 is en het y-afsnijpunt (0,c). De evaluatie van een willekeurige waarde voor x, zoals x = 2, levert c op.
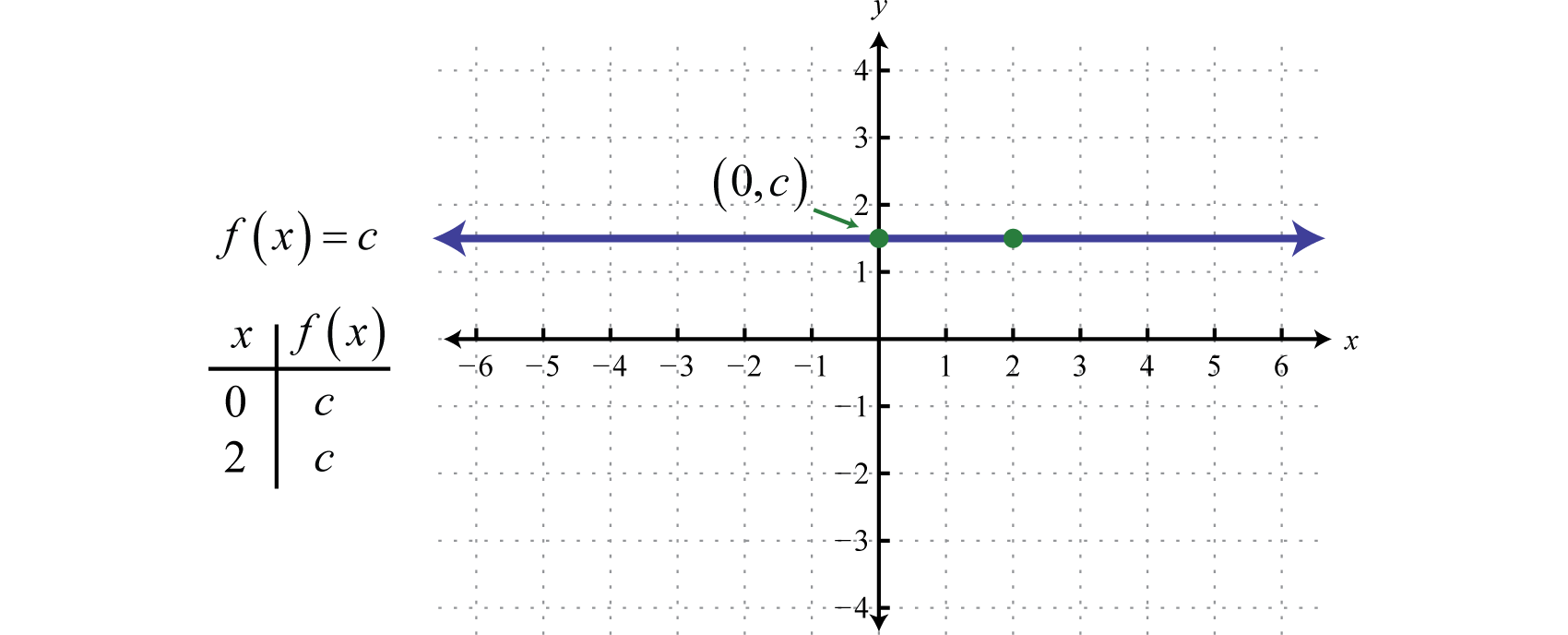
De grafiek van een constante functie is een horizontale lijn. Het domein bestaat uit alle reële getallen ℝ en het bereik uit de enkele waarde {c}.
Wij definiëren nu de identiteitsfunctieDe lineaire functie gedefinieerd door f(x)=x. f(x)=x. De evaluatie van een willekeurige waarde voor x zal resulteren in diezelfde waarde. Bijvoorbeeld, f(0)=0 en f(2)=2. De identiteitsfunctie is lineair, f(x)=1x+0, met helling m=1 en y-afsnijpunt (0, 0).
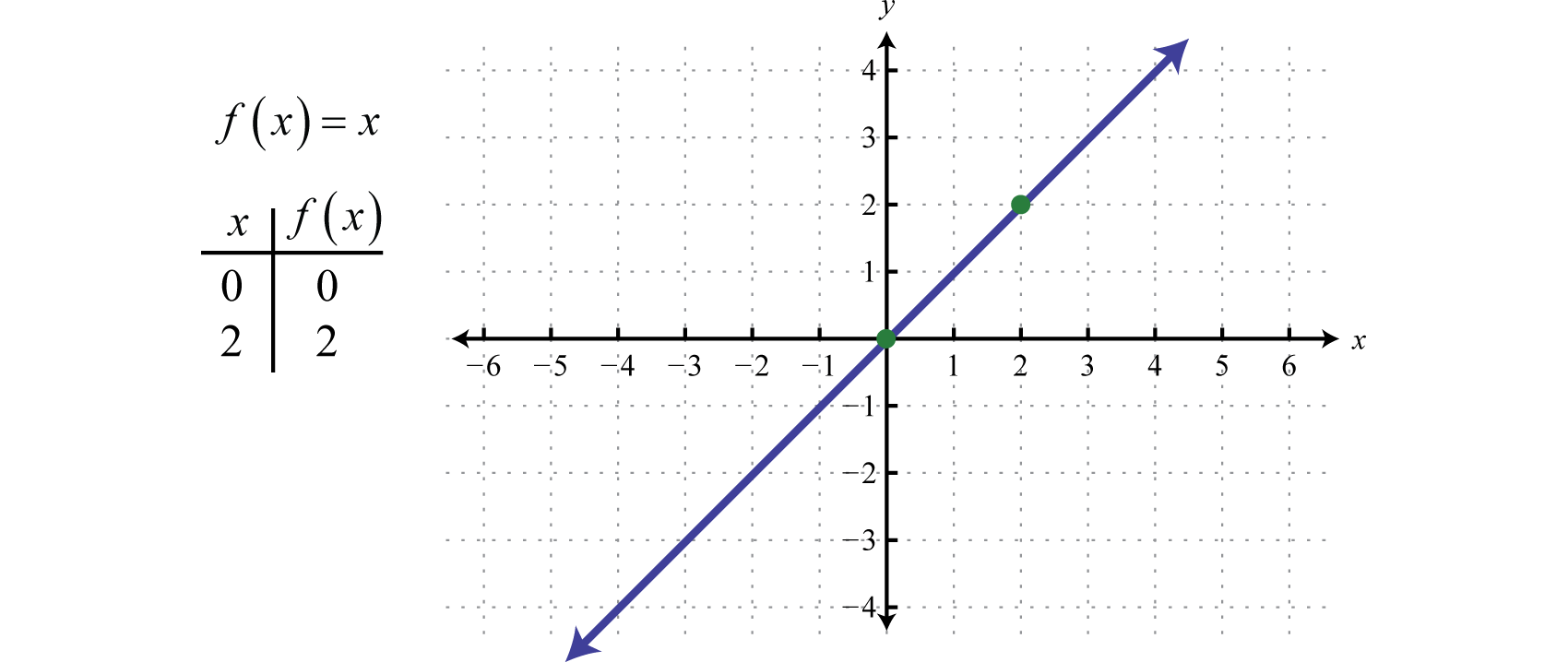
Het domein en bereik bestaan beide uit alle reële getallen.
De kwadratische functieDe kwadratische functie gedefinieerd door f(x)=x2., gedefinieerd door f(x)=x2, is de functie die wordt verkregen door de waarden in het domein te kwadrateren. Bijvoorbeeld, f(2)=(2)2=4 en f(-2)=(-2)2=4. Het resultaat van de kwadratuur van niet-nulwaarden in het domein zal altijd positief zijn.
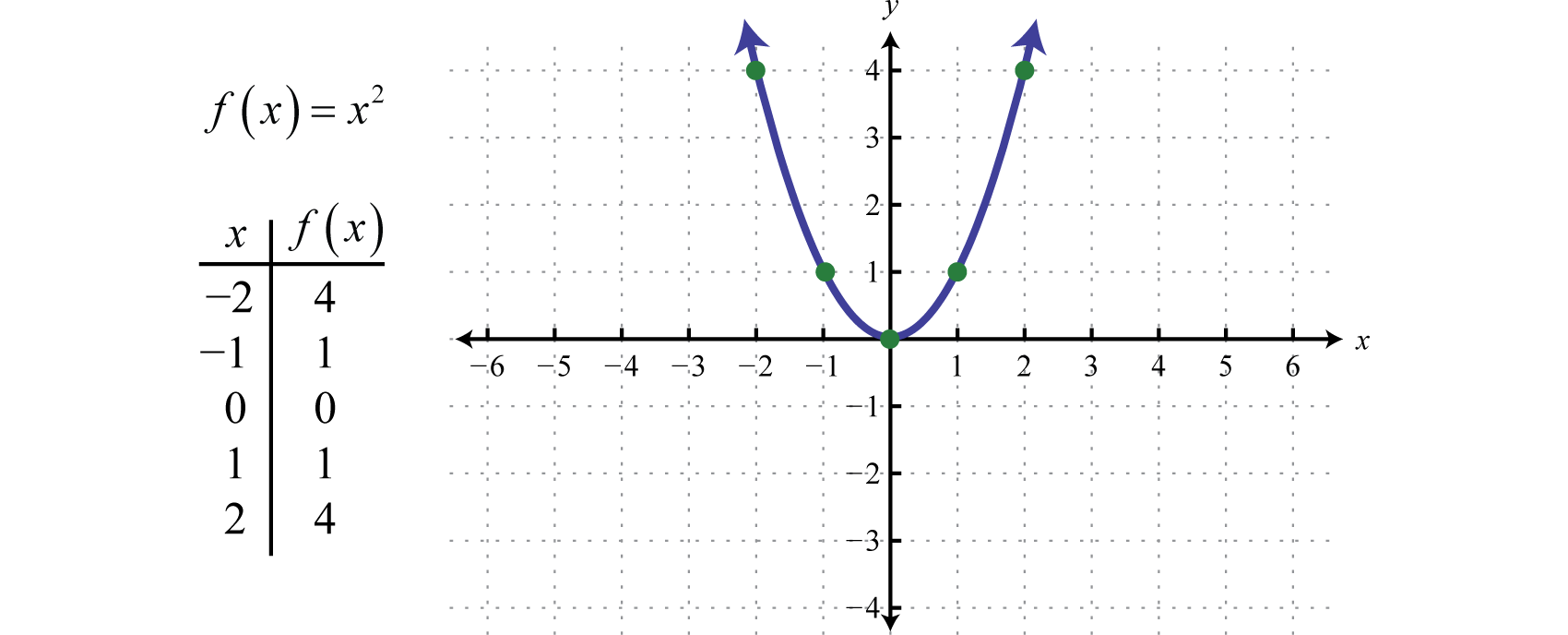
De resulterende kromme grafiek heet een paraboolDe kromme grafiek gevormd door de kwadratuurfunctie.. Het domein bestaat uit alle reële getallen ℝ en het bereik uit alle y-waarden groter dan of gelijk aan nul [0,∞).
De kwadrateerfunctieDe kwadrateerfunctie, gedefinieerd door f(x)=x3., gedefinieerd door f(x)=x3, verheft alle waarden in het domein tot de derde macht. De uitkomst kan zowel positief, nul als negatief zijn. Bijvoorbeeld, f(1)=(1)3=1, f(0)=(0)3=0, en f(-1)=(-1)3=-1.
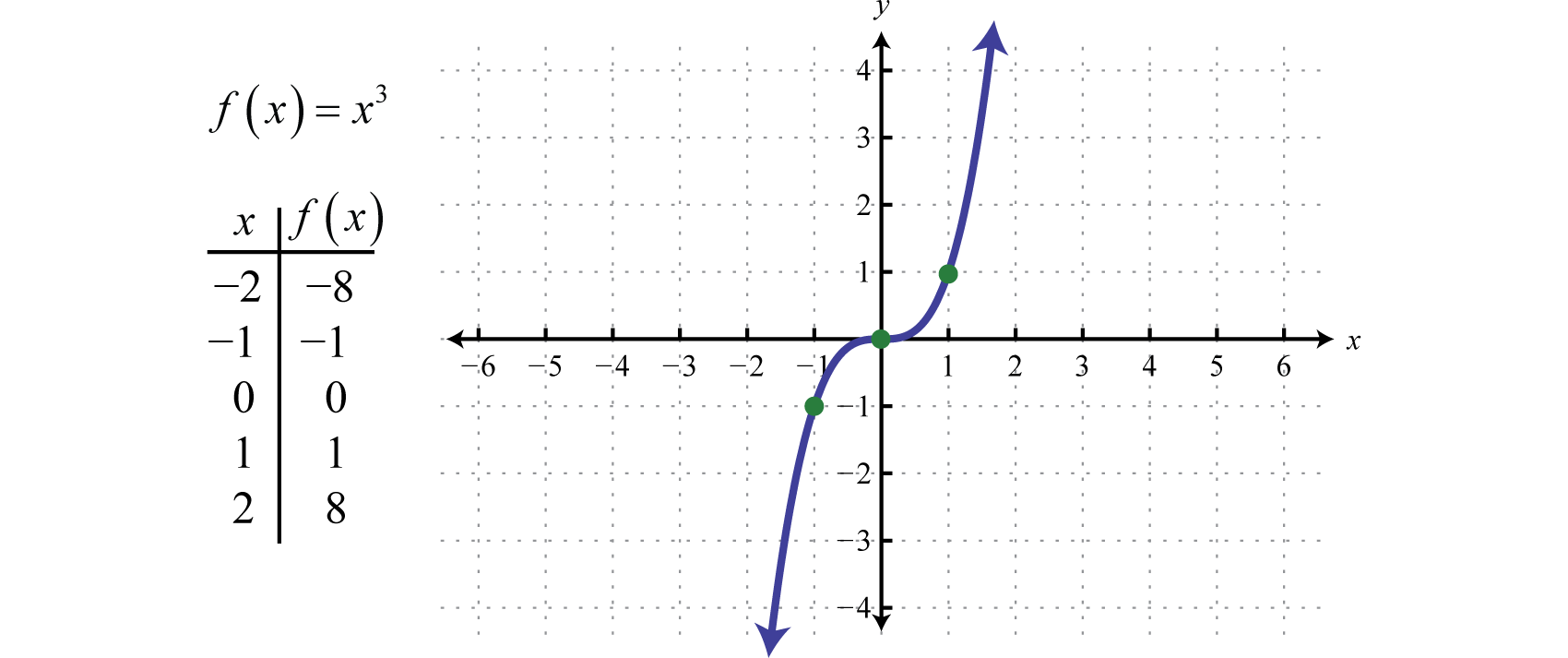
Het domein en bereik bestaan beide uit alle reële getallen ℝ.
Merk op dat de constante, de identiteit, de kwadratuur en de derdemachtsfuncties alle voorbeelden zijn van polynomiale basisfuncties. De volgende drie basisfuncties zijn geen polynomen.
De absolute-waardefunctieDe functie gedefinieerd door f(x)=|x|., gedefinieerd door f(x)=|x|, is een functie waarbij de output de afstand tot de oorsprong op een getallenlijn voorstelt. Het resultaat van de evaluatie van de absolute-waardefunctie voor elke niet-nulwaarde van x zal altijd positief zijn. Bijvoorbeeld, f(-2)=|-2|=2 en f(2)=|2|=2.
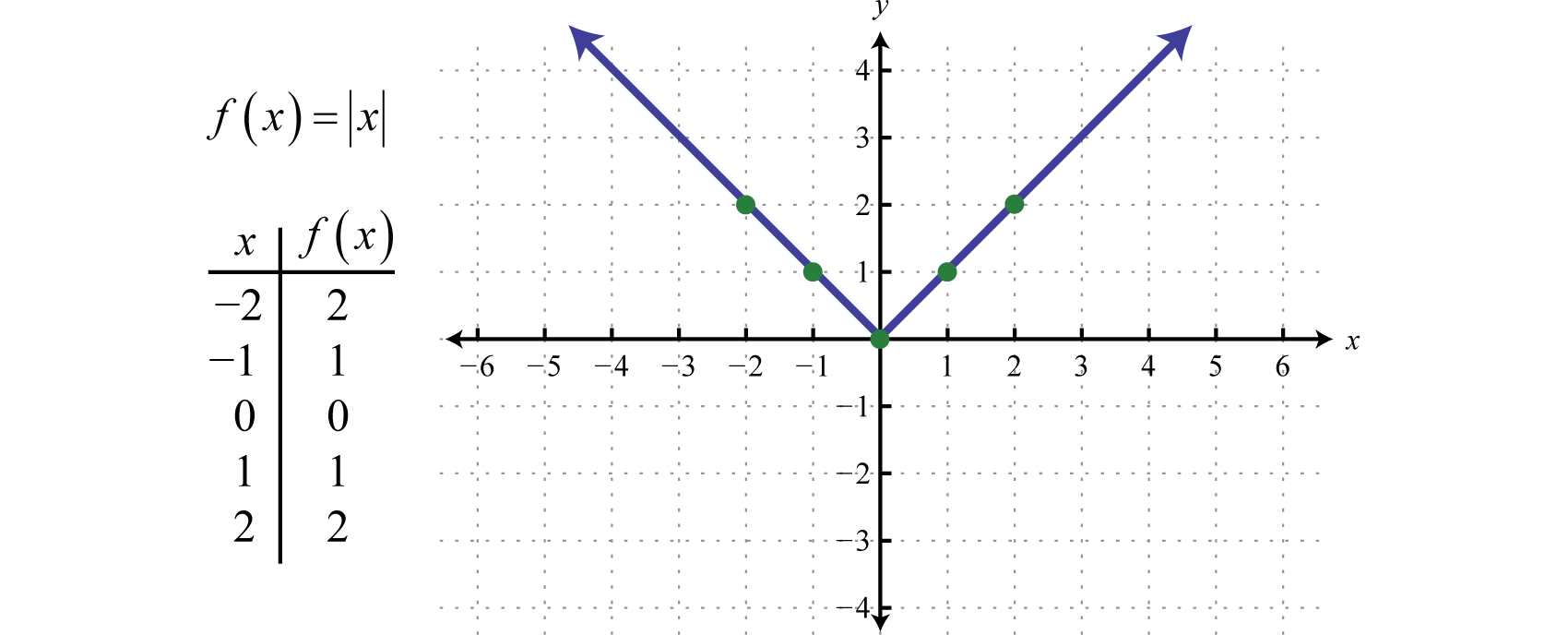
Het domein van de absolute-waardefunctie bestaat uit alle reële getallen ℝ en het bereik bestaat uit alle y-waarden groter dan of gelijk aan nul [0,∞).
De vierkantswortelfunctieDe functie gedefinieerd door f(x)=x, gedefinieerd door f(x)=x, is niet gedefinieerd als een reëel getal als de x-waarden negatief zijn. Daarom is de kleinste waarde in het domein nul. Bijvoorbeeld, f(0)=0=0 en f(4)=4=2.
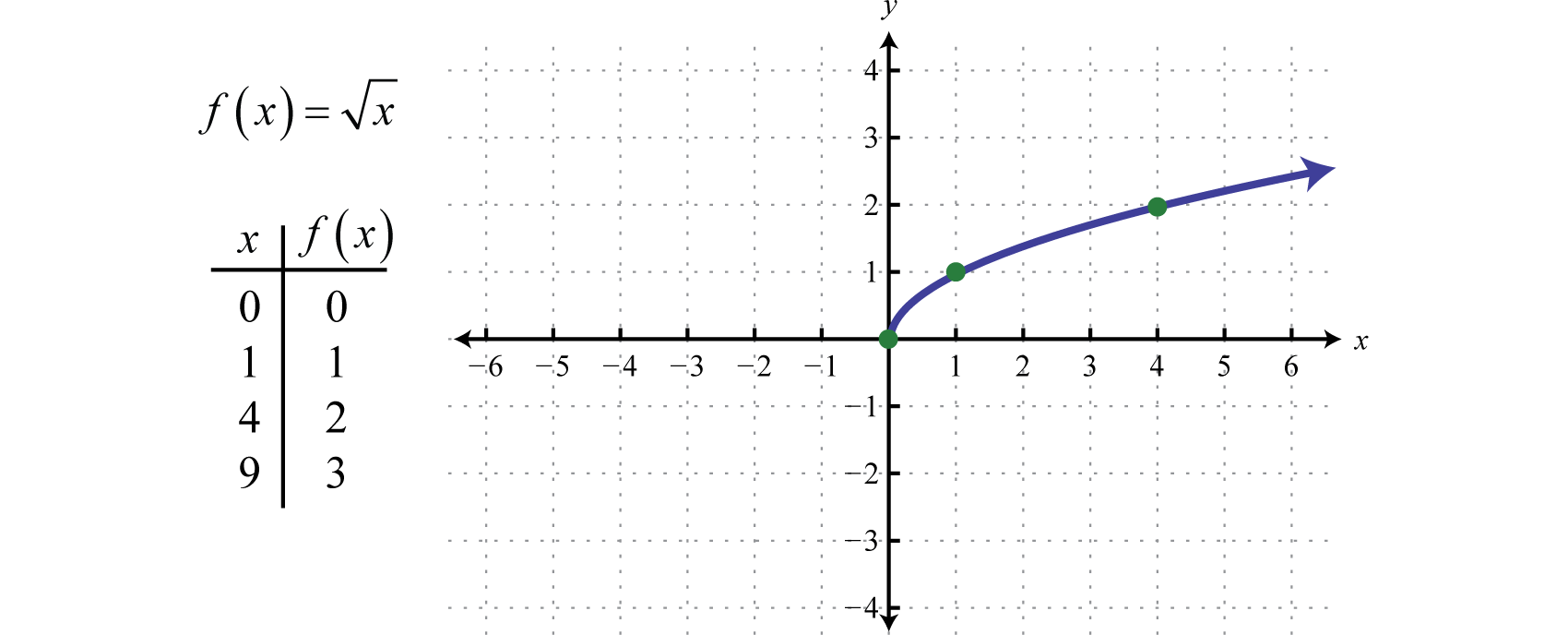
Het domein en bereik bestaan beide uit reële getallen groter dan of gelijk aan nul [0,∞).
De reciproke functieDe functie gedefinieerd door f(x)=1x., gedefinieerd door f(x)=1x, is een rationale functie met één restrictie op het domein, namelijk x≠0. De reciproke van een x-waarde zeer dicht bij nul is zeer groot. Bijvoorbeeld,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1.000)=1(11.000)=1⋅1.0001=1.000
Met andere woorden, naarmate de x-waarden dichter bij nul komen, zullen hun reciprocalen naar ofwel positieve ofwel negatieve oneindigheid neigen. Dit beschrijft een verticale asymptootEen verticale lijn waar een grafiek oneindig dicht bij komt. op de y-as. Bovendien is, wanneer de x-waarden zeer groot zijn, het resultaat van de reciproke functie zeer klein.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11.000=0,001
Met andere woorden, wanneer de x-waarden zeer groot worden, neigen de resulterende y-waarden naar nul. Dit beschrijft een horizontale asymptootEen horizontale lijn waar een grafiek oneindig dicht bij komt te liggen als de x-waarden naar ±∞ neigen. op de x-as. Na het uitzetten van een aantal punten kan de algemene vorm van de reciproke functie worden bepaald.
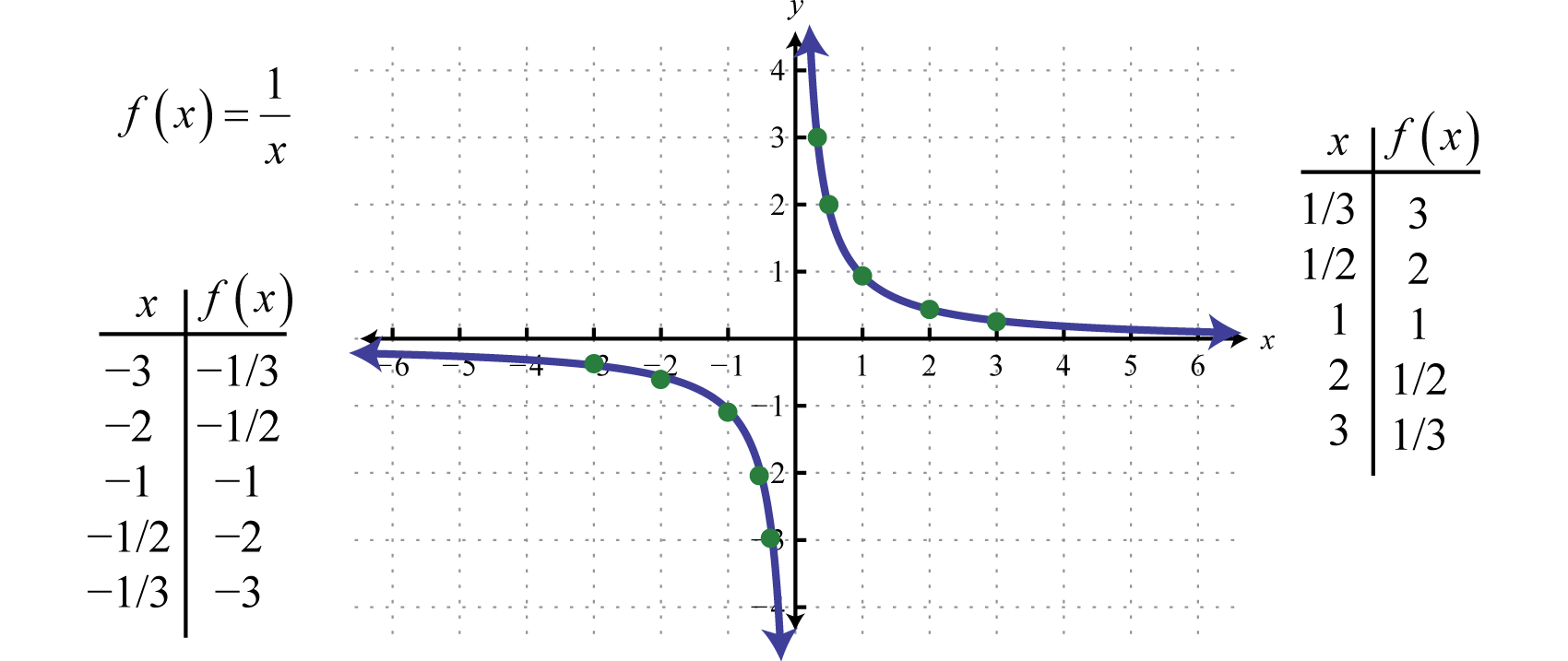
Zowel het domein als het bereik van de reciproke functie bestaat uit alle reële getallen behalve 0, dat als volgt met intervalnotatie kan worden uitgedrukt: (-∞,0)∪(0,∞).
