Accelerazione costante
L’analisi del moto bidimensionale di un proiettile si fa dividendolo in due moti: lungo gli assi orizzontale e verticale.
Obiettivi di apprendimento
Analizzare il moto di un proiettile bidimensionale lungo gli assi orizzontale e verticale
Punti chiave
Punti chiave
- L’accelerazione costante nel moto in due dimensioni segue generalmente un modello di proiettile.
- Il moto del proiettile è il moto di un oggetto lanciato o proiettato in aria, soggetto solo all’accelerazione (verticale) dovuta alla gravità.
- Analizziamo il moto bidimensionale del proiettile scomponendolo in due moti unidimensionali indipendenti lungo gli assi verticale e orizzontale.
Termini chiave
- cinematico: di o relativo al movimento o alla cinematica
Il moto del proiettile è il moto di un oggetto lanciato, o proiettato, in aria, soggetto solo alla forza di gravità. L’oggetto è chiamato proiettile e il suo percorso è chiamato traiettoria. Il moto di caduta degli oggetti è un semplice tipo unidimensionale di moto del proiettile in cui non c’è movimento orizzontale. Nel moto bidimensionale del proiettile, come quello di un pallone da calcio o di un altro oggetto lanciato, c’è sia una componente verticale che una orizzontale del moto.
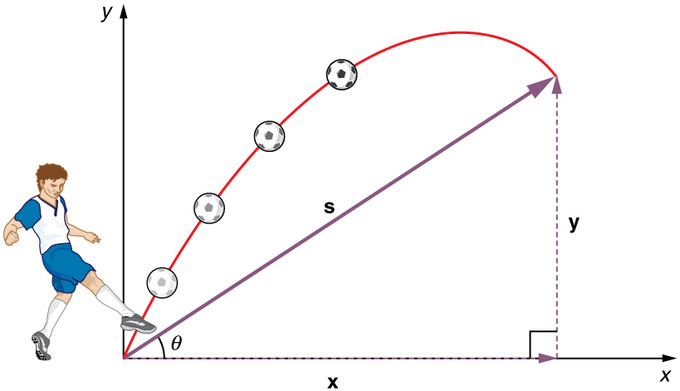
Movimento del proiettile: Lanciare un sasso o calciare un pallone generalmente produce un modello di moto proiettile che ha sia una componente verticale che una orizzontale.
Il fatto più importante da ricordare è che il moto lungo gli assi perpendicolari sono indipendenti e quindi possono essere analizzati separatamente. La chiave per analizzare il moto bidimensionale di un proiettile è di dividerlo in due moti, uno lungo l’asse orizzontale e l’altro lungo quello verticale. Per descrivere il moto dobbiamo occuparci della velocità e dell’accelerazione, oltre che dello spostamento.
Assumiamo che tutte le forze tranne la gravità (come la resistenza dell’aria e l’attrito, per esempio) siano trascurabili. Le componenti dell’accelerazione sono quindi molto semplici: \testo{a}_testo{y} = -\testo{g} = -9,81 \frac{\testo{m}}{\testo{s}^2} (assumiamo che il moto avvenga ad altezze abbastanza piccole vicino alla superficie della terra in modo che l’accelerazione dovuta alla gravità sia costante). Poiché l’accelerazione dovuta alla gravità è solo lungo la direzione verticale, \text{a}_\text{x} = 0. Quindi, le equazioni cinematiche che descrivono il moto lungo le direzioni \text{x} e \text{y} rispettivamente, possono essere usate:
{text{x} = \text{x}_0 + \text{v}_\text{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y}
Si analizza il moto bidimensionale del proiettile scomponendolo in due moti unidimensionali indipendenti lungo gli assi verticale e orizzontale. Il moto orizzontale è semplice, perché \text{a}_\text{x} = 0 e \text{v}_\text{x} è quindi costante. La velocità in direzione verticale comincia a diminuire man mano che un oggetto sale; nel suo punto più alto, la velocità verticale è zero. Quando un oggetto cade di nuovo verso la Terra, la velocità verticale aumenta di nuovo in grandezza ma punta nella direzione opposta alla velocità verticale iniziale. I moti x e y possono essere ricombinati per dare la velocità totale in qualsiasi punto della traiettoria.
