Funciones básicas
En esta sección graficamos siete funciones básicas que se utilizarán a lo largo de este curso. Cada función se grafica trazando puntos. Recuerde que f(x)=y y, por lo tanto, f(x) e y pueden usarse indistintamente.
Cualquier función de la forma f(x)=c, donde c es un número real cualquiera, se llama función constanteCualquier función de la forma f(x)=c donde c es un número real.. Las funciones constantes son lineales y se pueden escribir f(x)=0x+c. En esta forma, está claro que la pendiente es 0 y la intersección y es (0,c). La evaluación de cualquier valor de x, como x = 2, dará como resultado c.
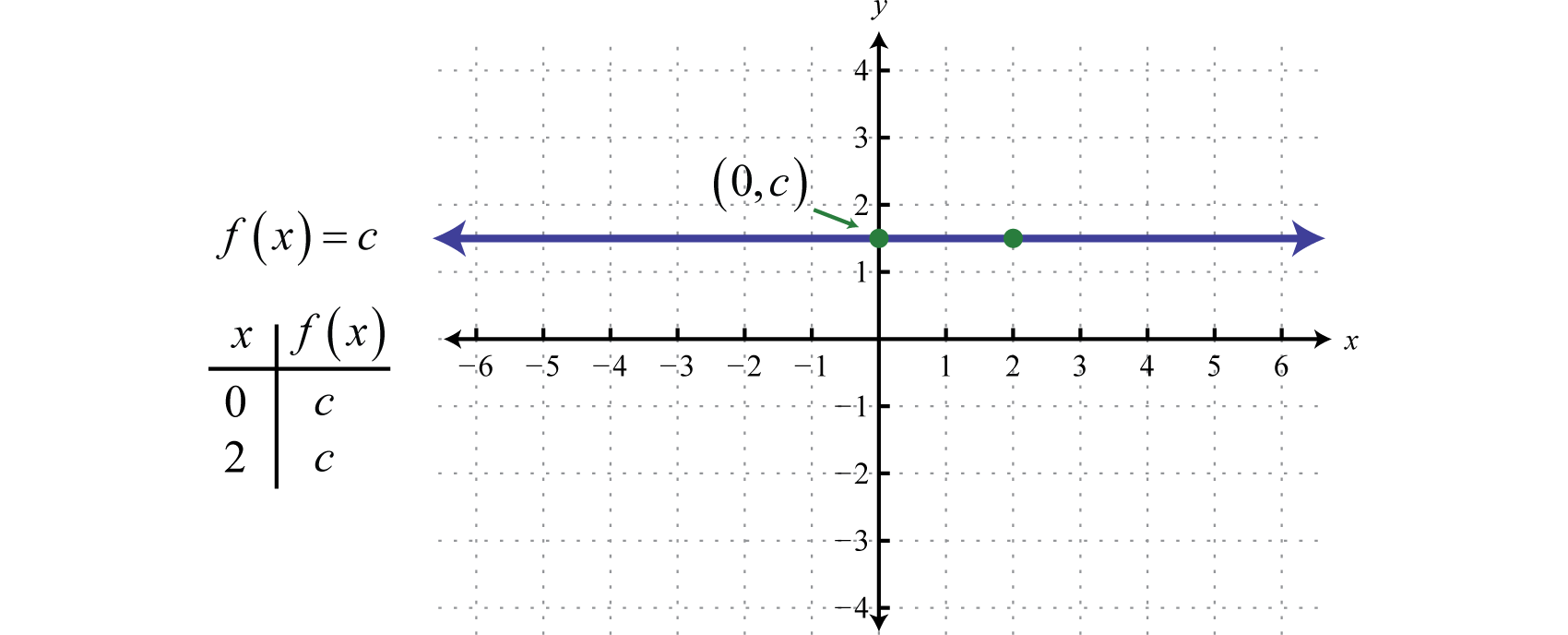
La gráfica de una función constante es una línea horizontal. El dominio consiste en todos los números reales ℝ y el rango consiste en el único valor {c}.
A continuación definimos la función identidadLa función lineal definida por f(x)=x. f(x)=x. La evaluación de cualquier valor de x dará como resultado ese mismo valor. Por ejemplo, f(0)=0 y f(2)=2. La función identidad es lineal, f(x)=1x+0, con pendiente m=1 e intersección y (0, 0).
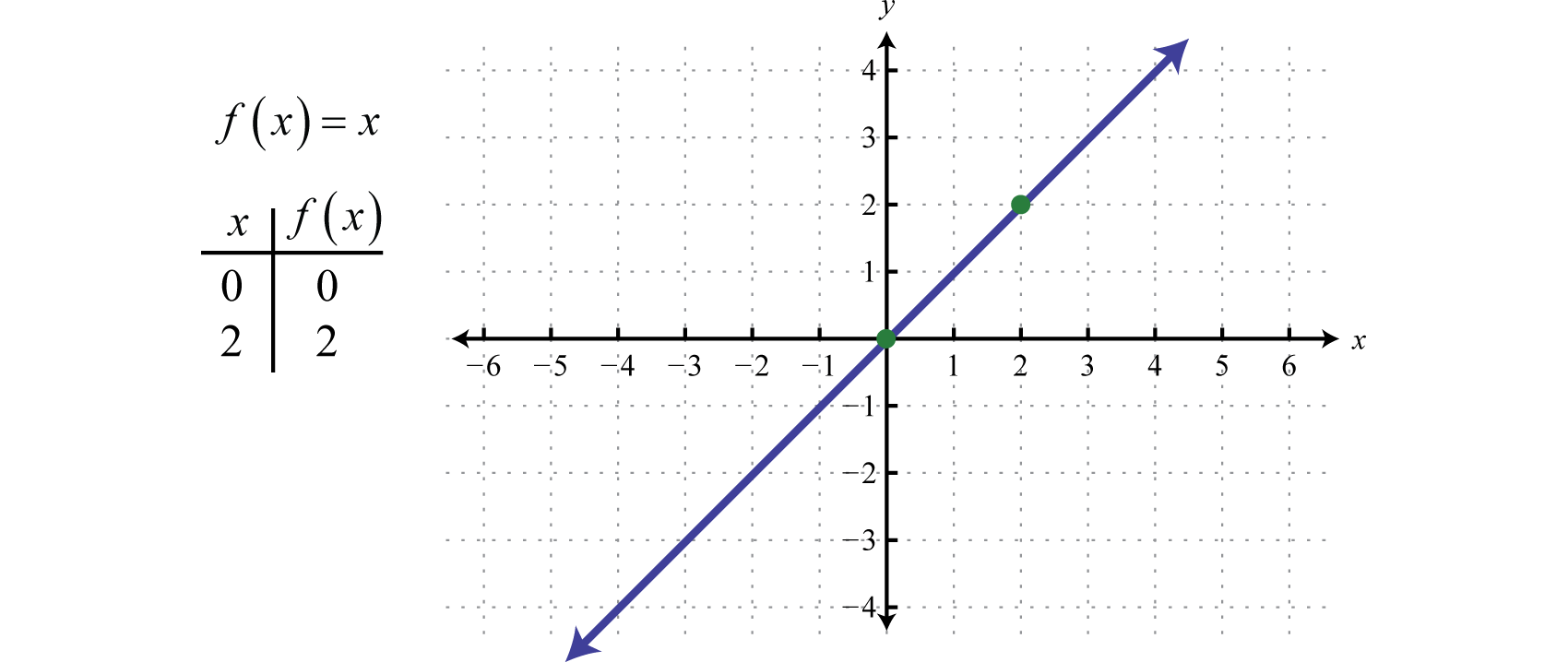
El dominio y el rango consisten en todos los números reales.
La función cuadrática definida por f(x)=x2., definida por f(x)=x2, es la función que se obtiene elevando al cuadrado los valores del dominio. Por ejemplo, f(2)=(2)2=4 y f(-2)=(-2)2=4. El resultado de elevar al cuadrado los valores no nulos del dominio será siempre positivo.
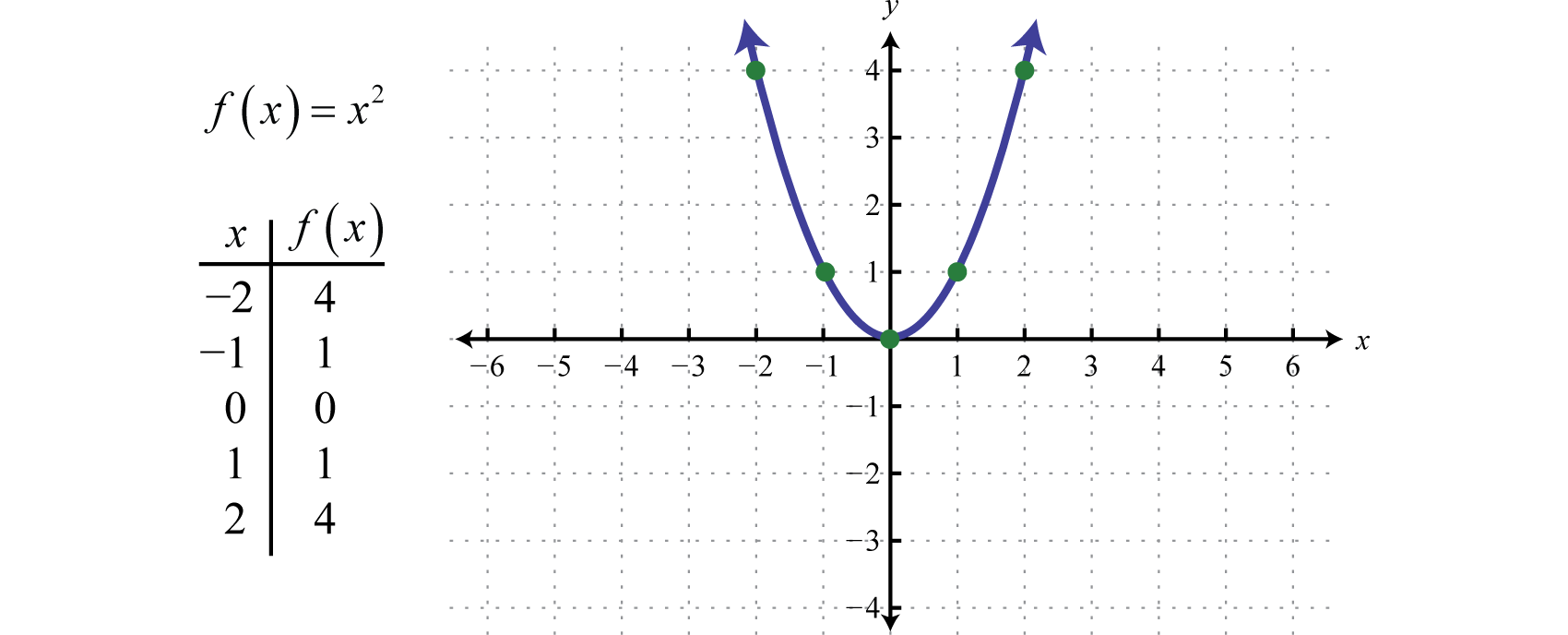
La gráfica curva resultante se llama parábolaLa gráfica curva formada por la función de elevación al cuadrado.. El dominio consiste en todos los números reales ℝ y el rango consiste en todos los valores de y mayores o iguales a cero [0,∞).
La función de cubicaciónLa función cúbica definida por f(x)=x3., definida por f(x)=x3, eleva todos los valores del dominio a la tercera potencia. El resultado puede ser positivo, cero o negativo. Por ejemplo, f(1)=(1)3=1, f(0)=(0)3=0, y f(-1)=(-1)3=-1.
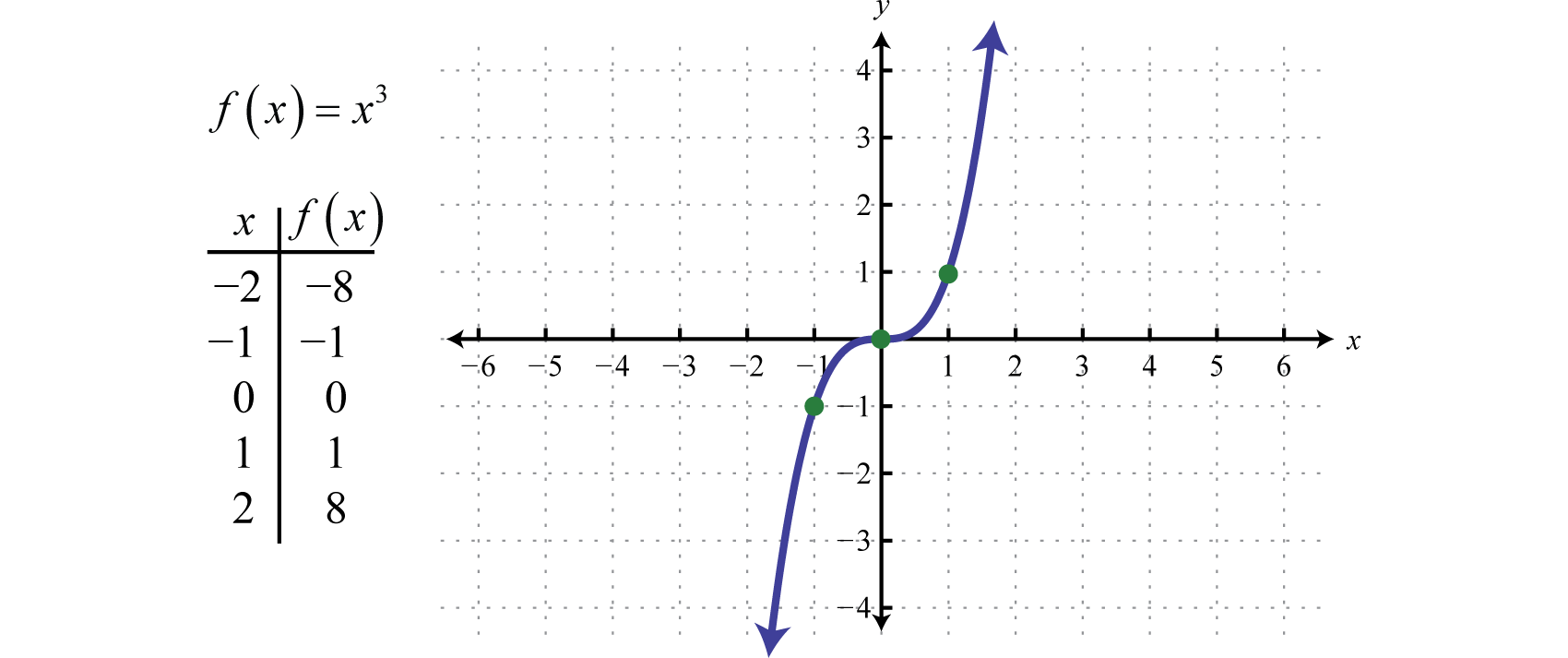
El dominio y el rango consisten en todos los números reales ℝ.
Nótese que la constante, la identidad, el cuadrado y el cubo son ejemplos de funciones polinómicas básicas. Las siguientes tres funciones básicas no son polinomios.
La función de valor absolutoLa función definida por f(x)=|x|., definida por f(x)=|x|, es una función donde la salida representa la distancia al origen en una recta numérica. El resultado de evaluar la función de valor absoluto para cualquier valor no nulo de x será siempre positivo. Por ejemplo, f(-2)=|-2|=2 y f(2)=|2|=2.
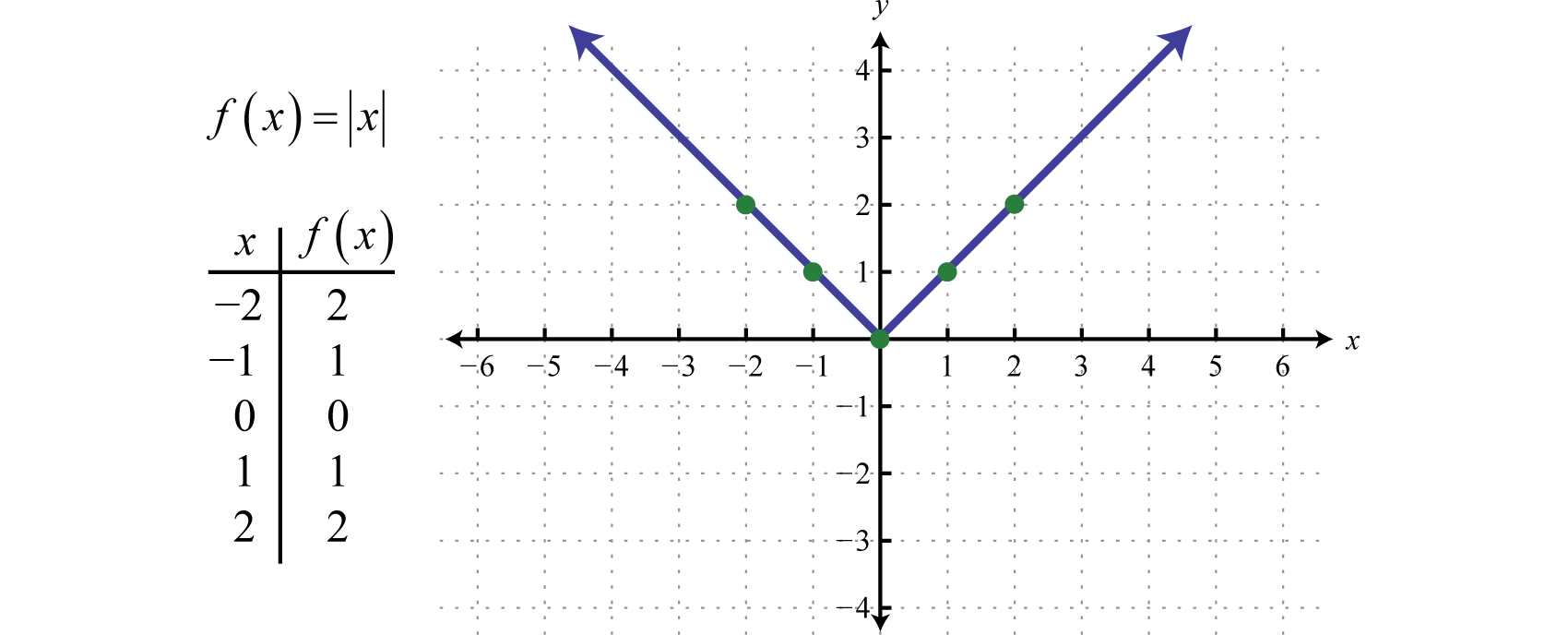
El dominio de la función valor absoluto consiste en todos los números reales ℝ y el rango consiste en todos los valores de y mayores o iguales a cero [0,∞).
La función raíz cuadradaLa función definida por f(x)=x., definida por f(x)=x, no está definida como un número real si los valores de x son negativos. Por lo tanto, el valor más pequeño en el dominio es cero. Por ejemplo, f(0)=0=0 y f(4)=4=2.
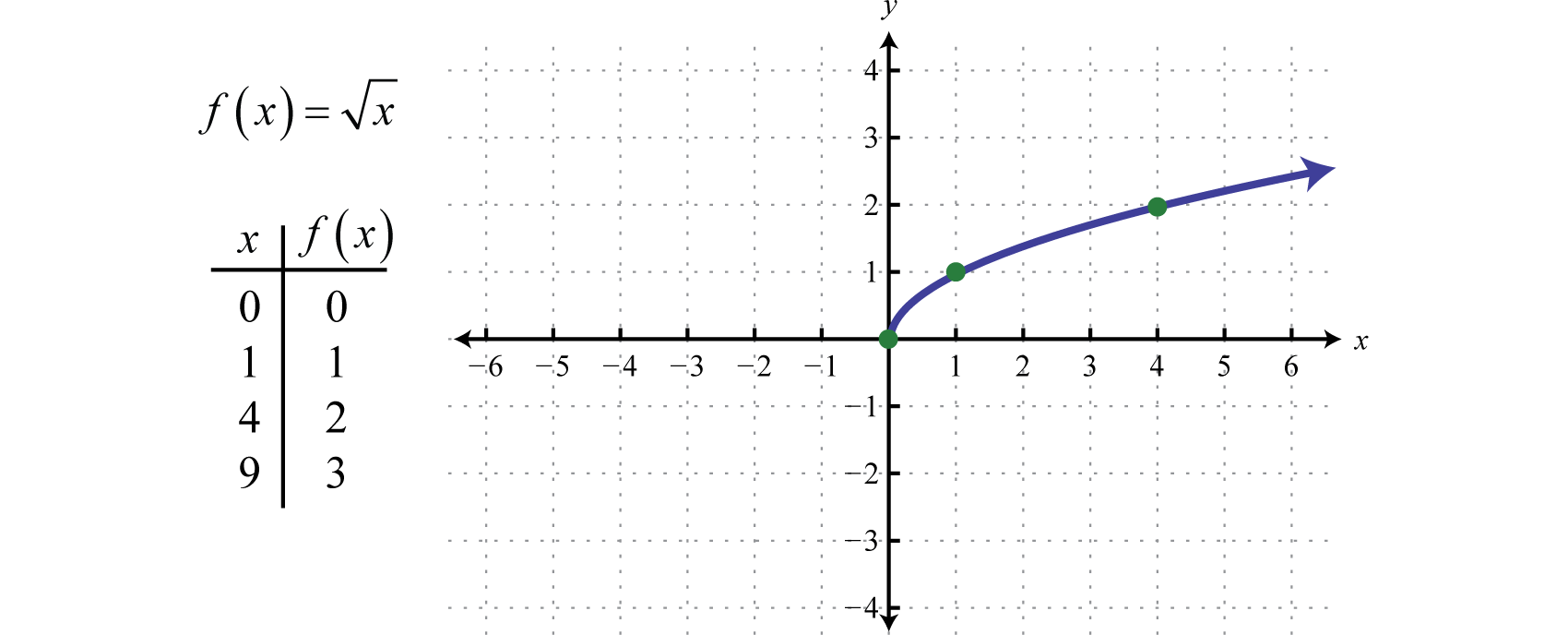
El dominio y el rango están formados por números reales mayores o iguales que cero [0,∞).
La función recíprocaLa función definida por f(x)=1x., definida por f(x)=1x, es una función racional con una restricción en el dominio, concretamente x≠0. El recíproco de un valor de x muy cercano a cero es muy grande. Por ejemplo,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1.000)=1(11.000)=1⋅1.0001=1.000
En otras palabras, a medida que los valores de x se acercan a cero sus recíprocos tenderán hacia el infinito positivo o negativo. Esto describe una asíntota verticalUna línea vertical a la que una gráfica se acerca infinitamente. en el eje y. Además, cuando los valores de x son muy grandes, el resultado de la función recíproca es muy pequeño.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11.000=0,001
En otras palabras, a medida que los valores de x son muy grandes, los valores de y resultantes tienden a cero. Esto describe una asíntota horizontalUna línea horizontal a la que una gráfica se acerca infinitamente donde los valores x tienden hacia ±∞ en el eje x. Después de trazar un número de puntos se puede determinar la forma general de la función recíproca.
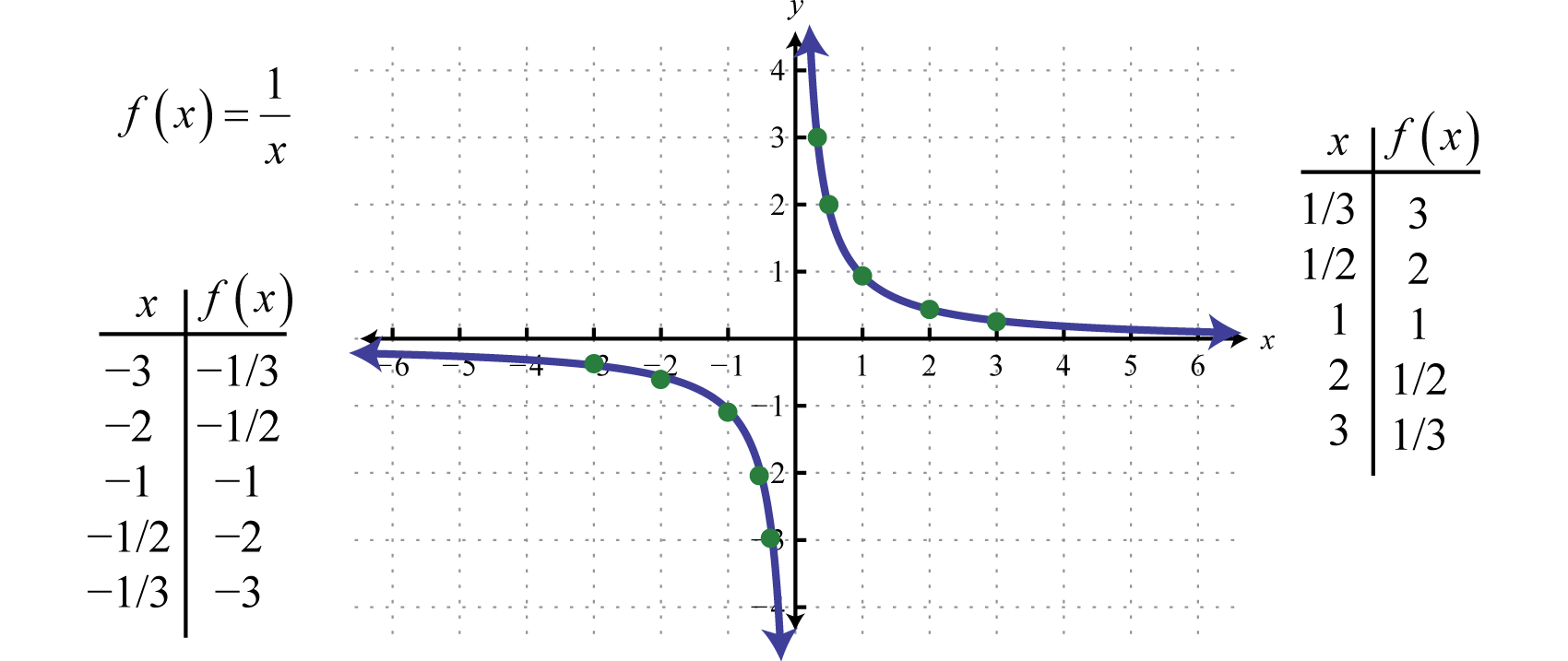
Tanto el dominio como el rango de la función recíproca consisten en todos los números reales excepto el 0, que se puede expresar usando la notación de intervalo como sigue: (-∞,0)∪(0,∞).
