Fonctions de base
Dans cette section, nous graphions sept fonctions de base qui seront utilisées tout au long de ce cours. Chaque fonction est représentée graphiquement en traçant des points. Rappelez-vous que f(x)=y et donc que f(x) et y peuvent être utilisés de façon interchangeable.
Toute fonction de la forme f(x)=c, où c est un nombre réel quelconque, est appelée une fonction constanteToute fonction de la forme f(x)=c où c est un nombre réel…. Les fonctions constantes sont linéaires et peuvent s’écrire f(x)=0x+c. Sous cette forme, il est clair que la pente est 0 et que l’ordonnée à l’origine est (0,c). L’évaluation de n’importe quelle valeur de x, comme x = 2, donnera c.
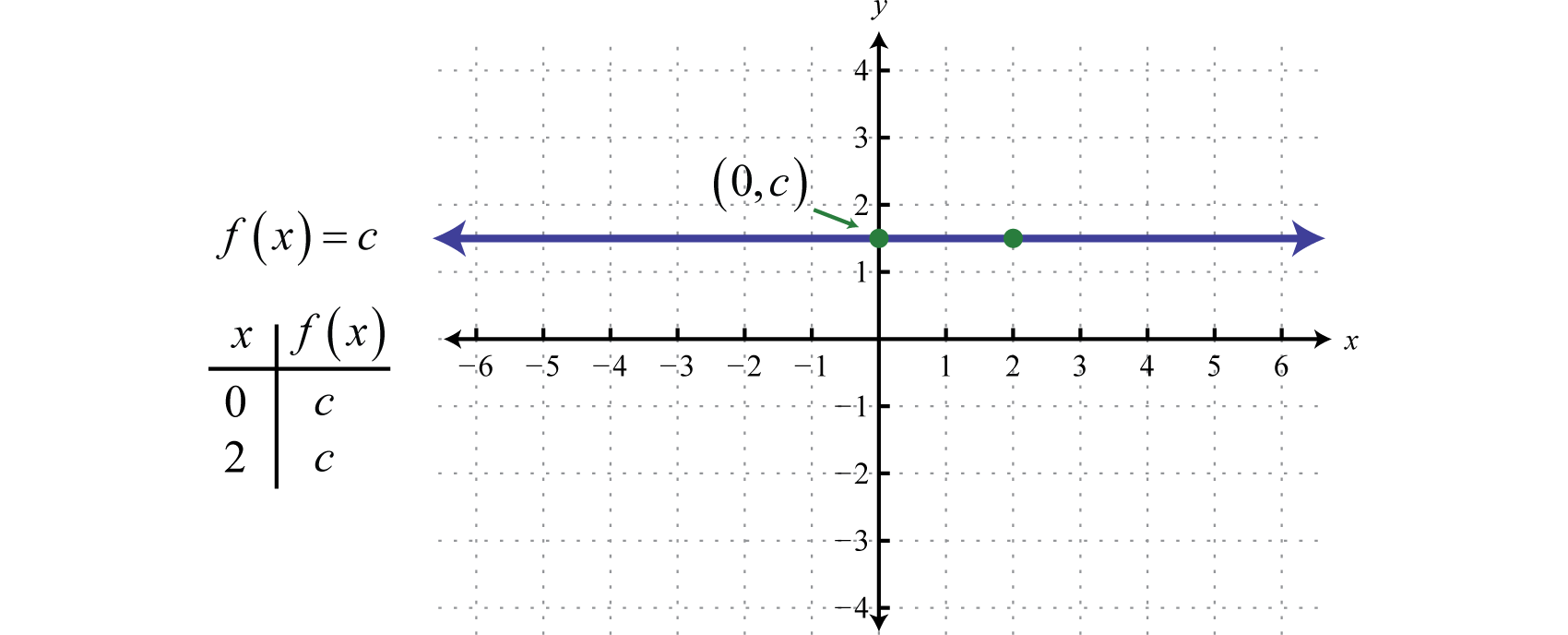
Le graphique d’une fonction constante est une ligne horizontale. Le domaine est constitué de tous les nombres réels ℝ et l’étendue est constituée de la seule valeur {c}.
Nous définissons ensuite la fonction identitéLa fonction linéaire définie par f(x)=x. f(x)=x. L’évaluation de n’importe quelle valeur pour x donnera cette même valeur. Par exemple, f(0)=0 et f(2)=2. La fonction identité est linéaire, f(x)=1x+0, avec une pente m=1 et un ordonnée à l’origine (0, 0).
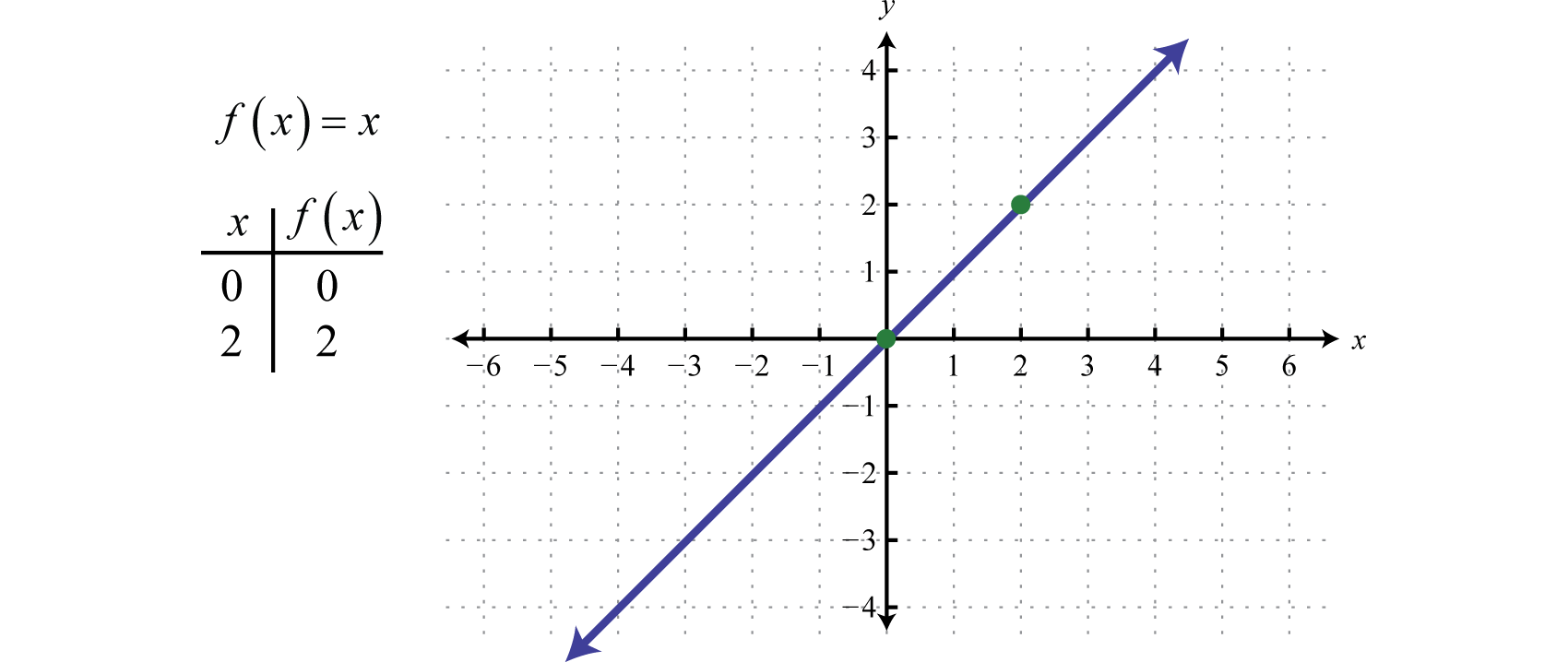
Le domaine et l’étendue consistent tous deux en tous les nombres réels.
La fonction d’élévation au carréLa fonction quadratique définie par f(x)=x2., définie par f(x)=x2, est la fonction obtenue en élevant au carré les valeurs du domaine. Par exemple, f(2)=(2)2=4 et f(-2)=(-2)2=4. Le résultat de l’élévation au carré des valeurs non nulles du domaine sera toujours positif.
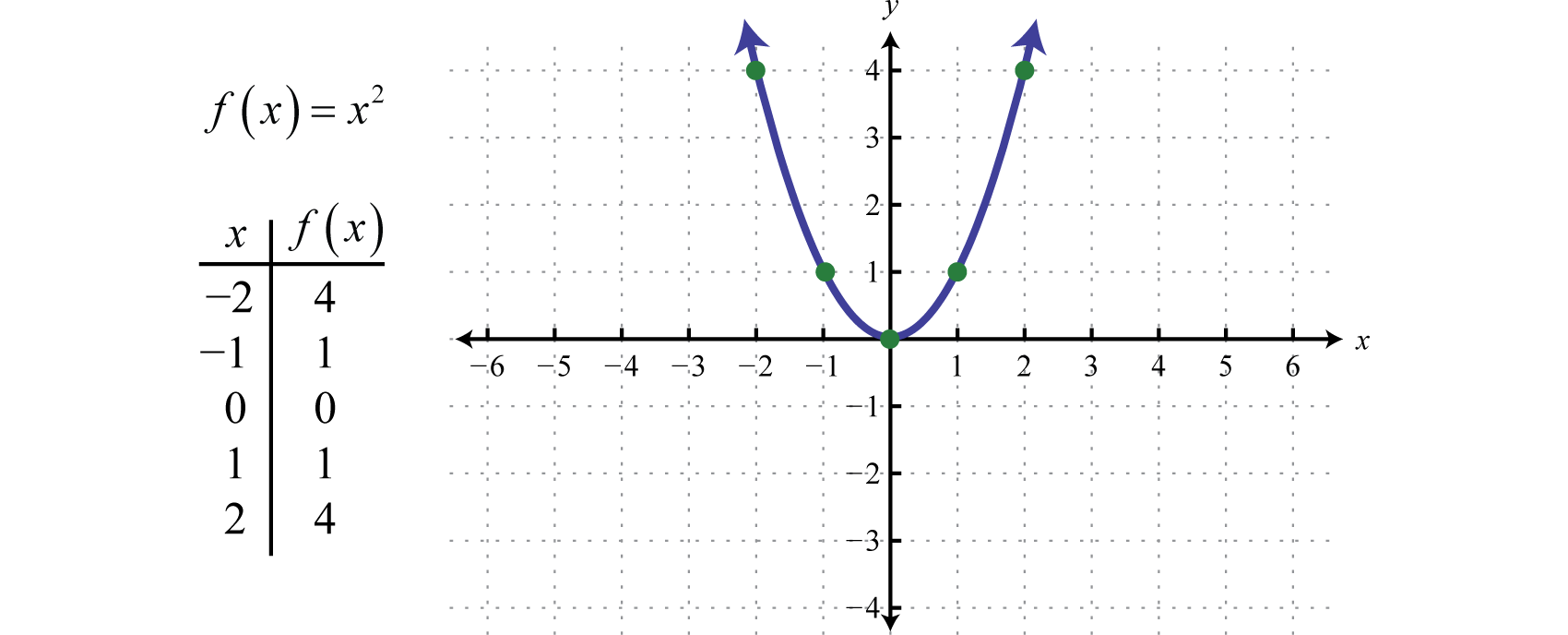
Le graphique courbe résultant est appelé paraboleLe graphique courbe formé par la fonction d’élévation au carré…. Le domaine est constitué de tous les nombres réels ℝ et l’étendue est constituée de toutes les valeurs de y supérieures ou égales à zéro [0,∞).
La fonction cubiqueLa fonction cubique définie par f(x)=x3., définie par f(x)=x3, élève toutes les valeurs du domaine à la troisième puissance. Les résultats peuvent être soit positifs, soit nuls, soit négatifs. Par exemple, f(1)=(1)3=1, f(0)=(0)3=0, et f(-1)=(-1)3=-1.
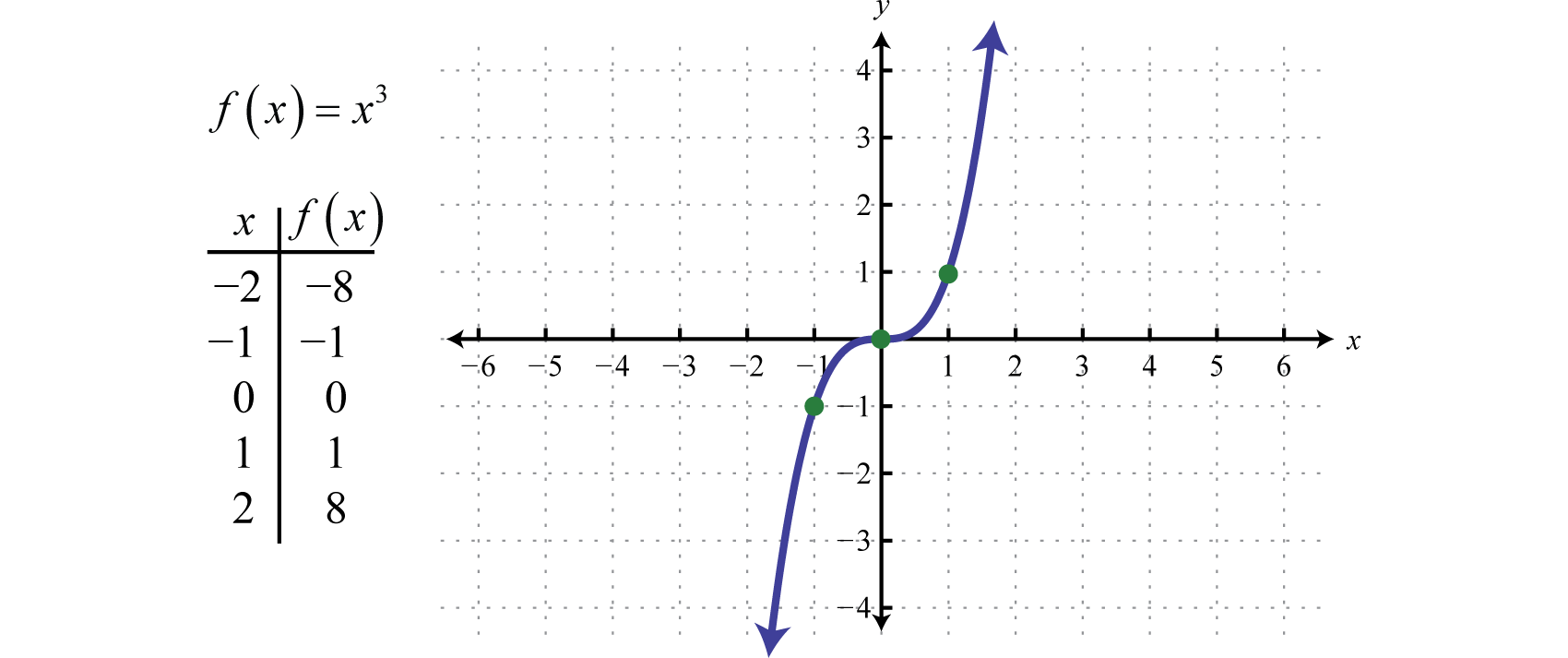
Le domaine et l’étendue sont tous deux constitués de tous les nombres réels ℝ.
Notez que les fonctions constante, identité, quadrature et cubage sont toutes des exemples de fonctions polynomiales de base. Les trois fonctions de base suivantes ne sont pas des polynômes.
La fonction valeur absolueLa fonction définie par f(x)=|x|., définie par f(x)=|x|, est une fonction dont la sortie représente la distance à l’origine sur une droite numérique. Le résultat de l’évaluation de la fonction valeur absolue pour toute valeur non nulle de x sera toujours positif. Par exemple, f(-2)=|-2|=2 et f(2)=|2|=2.
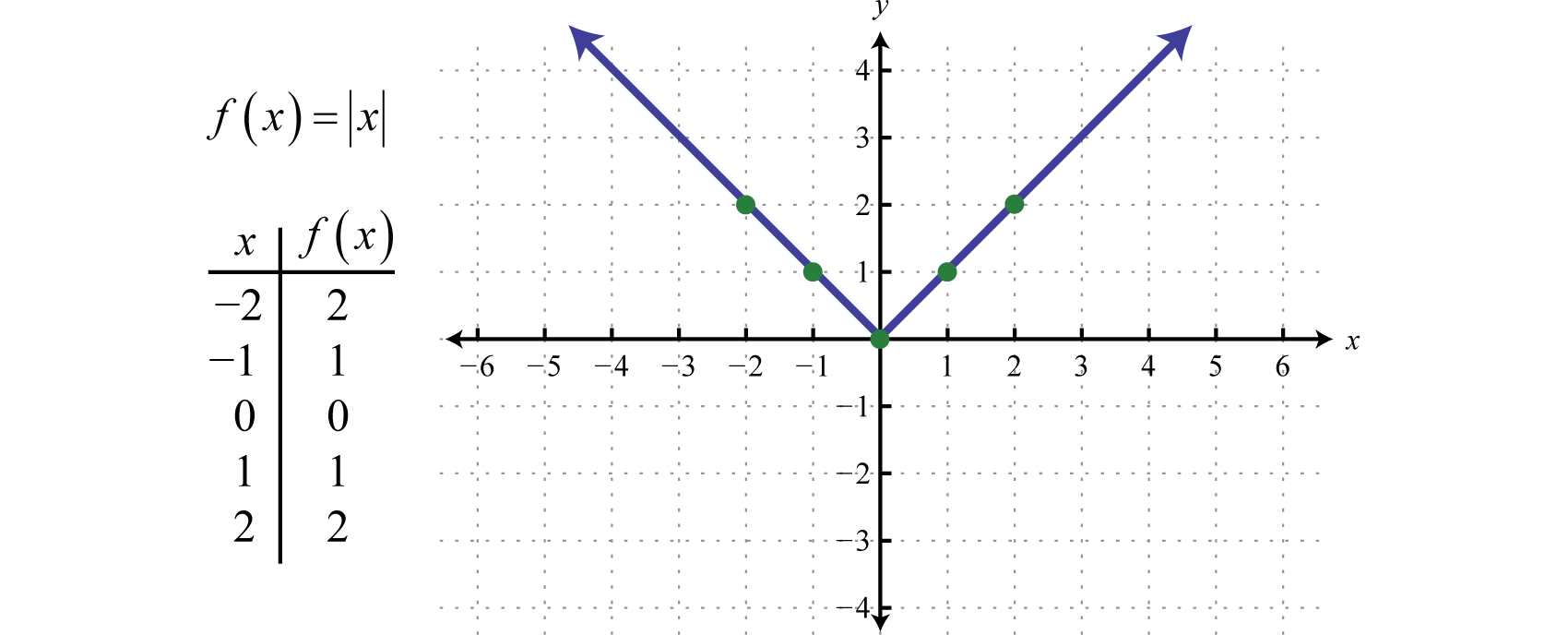
Le domaine de la fonction valeur absolue est constitué de tous les nombres réels ℝ et l’étendue est constituée de toutes les valeurs de y supérieures ou égales à zéro [0,∞).
La fonction racine carréeLa fonction définie par f(x)=x.., définie par f(x)=x, n’est pas définie comme étant un nombre réel si les valeurs de x sont négatives. Par conséquent, la plus petite valeur du domaine est zéro. Par exemple, f(0)=0=0 et f(4)=4=2.
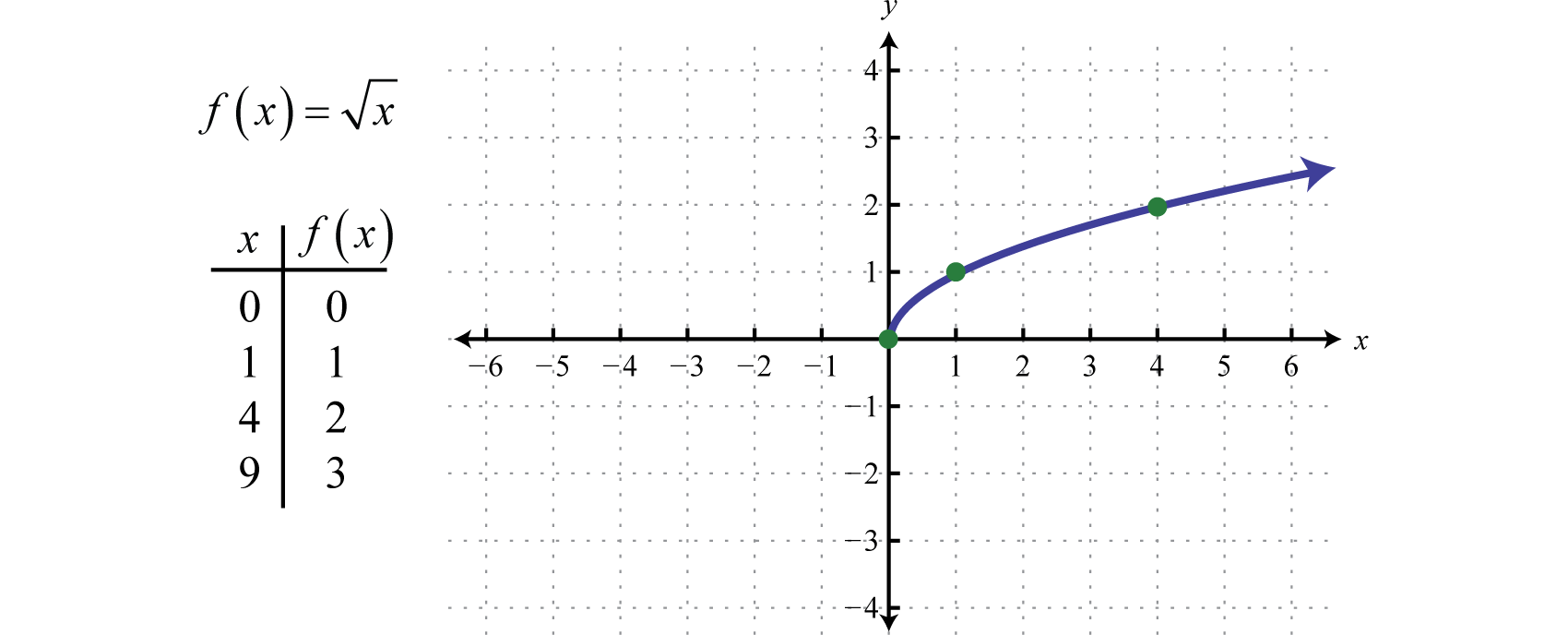
Le domaine et l’étendue sont tous deux constitués de nombres réels supérieurs ou égaux à zéro [0,∞).
La fonction réciproqueLa fonction définie par f(x)=1x., définie par f(x)=1x, est une fonction rationnelle avec une restriction sur le domaine, à savoir x≠0. La réciproque d’une valeur de x très proche de zéro est très grande. Par exemple,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1,000)=1(11,000)=1⋅1,0001=1,000
En d’autres termes, à mesure que les valeurs x s’approchent de zéro, leurs réciproques tendront vers l’infini positif ou négatif. Ceci décrit une asymptote verticaleLigne verticale dont un graphique se rapproche à l’infini. sur l’axe des ordonnées. De plus, lorsque les valeurs x sont très grandes, le résultat de la fonction réciproque est très petit.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11 000=0,001
En d’autres termes, lorsque les valeurs x deviennent très grandes, les valeurs y résultantes tendent vers zéro. Ceci décrit une asymptote horizontaleLigne horizontale dont un graphique se rapproche à l’infini lorsque les valeurs de x tendent vers ±∞. à l’axe des x. Après avoir tracé un certain nombre de points, on peut déterminer la forme générale de la fonction réciproque.
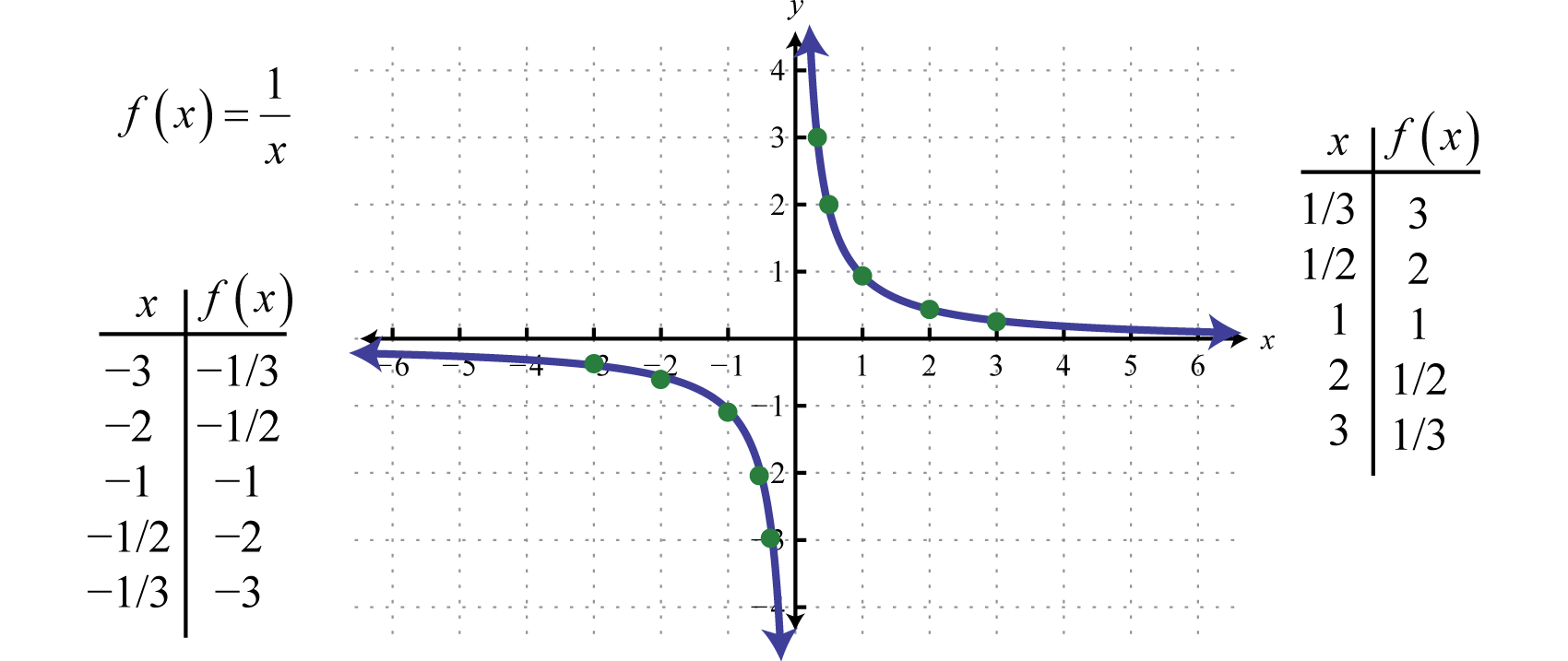
Le domaine et l’étendue de la fonction réciproque sont tous deux constitués de tous les nombres réels sauf 0, qui peut être exprimé en utilisant la notation d’intervalle comme suit : (-∞,0)∪(0,∞).
