Konstantti kiihtyvyys
Kaksiulotteisen ammuksen liikkeen analysointi tapahtuu jakamalla se kahteen liikkeeseen: vaaka- ja pystyakselilla.
Oppimistavoitteet
Analysoidaan kaksiulotteista projektiilin liikettä vaaka- ja pystyakseleita pitkin
Keskeiset opit
Keskeiset kohdat
- Kahdessa ulottuvuudessa tapahtuvassa liikkeessä jatkuva kiihtyvyys noudattelee tavallisesti projektiilin mallia.
- Projektioliike on ilmaan heitetyn tai projisoidun kappaleen liike, johon kohdistuu vain painovoiman aiheuttama (pystysuora) kiihtyvyys.
- Analysoimme kaksiulotteista projektioliikettä pilkkomalla sen kahdeksi itsenäiseksi yksiulotteiseksi liikkeeksi pysty- ja vaaka-akselilla.
Avaintermit
- kinemaattinen: liikettä tai kinematiikkaa koskeva tai siihen liittyvä
Projektioliike on ilmaan heitetyn tai projisoidun kappaleen liikettä, johon kohdistuu vain painovoima. Esinettä kutsutaan ammukseksi, ja sen kulkua kutsutaan sen lentoradaksi. Putoavien kappaleiden liike on yksinkertainen yksiulotteinen ammuksen liiketyyppi, jossa ei ole vaakasuuntaista liikettä. Kaksiulotteisessa projektiilin liikkeessä, kuten jalkapallon tai muun heitetyn esineen liikkeessä, liikkeessä on sekä pysty- että vaakakomponentti.
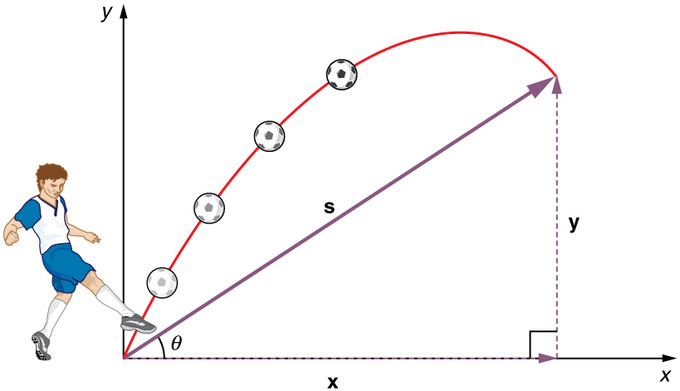
Projektiilin liike: Kiven heittäminen tai pallon potkaiseminen tuottaa yleensä ammuksen kaltaisen liikkeen, jossa on sekä pysty- että vaakakomponentti.
Tärkein muistettava seikka on, että kohtisuoraan toisiaan vastaan kohtisuorassa olevien akselien suuntaiset liikkeet ovat toisistaan riippumattomia, ja siten niitä voidaan analysoida erikseen. Avain kaksiulotteisen ammuksen liikkeen analysointiin on jakaa se kahteen liikkeeseen, joista toinen on vaaka-akselin suuntainen ja toinen pystyakselin suuntainen. Liikkeen kuvaamiseksi meidän on käsiteltävä nopeutta ja kiihtyvyyttä sekä siirtymää.
Oletamme, että kaikki voimat painovoimaa lukuun ottamatta (kuten esimerkiksi ilmanvastus ja kitka) ovat merkityksettömiä. Kiihtyvyyden komponentit ovat tällöin hyvin yksinkertaisia: \text{a}_\text{y} = -\text{g} = -9.81 \frac{\text{m}}{\text{s}^2} (oletamme, että liike tapahtuu riittävän pienillä korkeuksilla lähellä maan pintaa, jotta painovoiman aiheuttama kiihtyvyys on vakio). Koska painovoiman aiheuttama kiihtyvyys on vain pystysuunnassa, \text{a}_\text{x} = 0. Näin ollen voidaan käyttää kinemaattisia yhtälöitä, jotka kuvaavat liikettä \text{x}- ja \text{y}-suunnissa:
\text{x} = \text{x}_0 + \text{v}_\text{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
\text{v}_\text{y}^2=\text{v}_{0\text{y}}^2+2\text{a}_\text{y}(\text{y}-\text{y}_0)
Analysoimme kaksiulotteista ammuksen liikettä pilkkomalla sen kahdeksi itsenäiseksi yksiulotteiseksi liikkeeksi pystysuoralla ja vaakasuoralla akselilla. Vaakasuora liike on yksinkertainen, koska \text{a}_\text{x} = 0 ja \text{v}_\text{x} on siten vakio. Pystysuuntainen nopeus alkaa pienentyä kappaleen noustessa; korkeimmillaan pystynopeus on nolla. Kun kappale putoaa jälleen kohti Maata, pystynopeus kasvaa jälleen suuruudeltaan, mutta osoittaa vastakkaiseen suuntaan kuin alkuperäinen pystynopeus. Liikkeet \text{x} ja \text{y} voidaan yhdistää uudelleen, jolloin saadaan kokonaisnopeus missä tahansa radan pisteessä.
