Grundfunktioner
I dette afsnit graferer vi syv grundfunktioner, som vil blive brugt i hele kurset. Hver funktion grafiseres ved at plotte punkter. Husk, at f(x)=y og dermed kan f(x) og y bruges i flæng.
En funktion af formen f(x)=c, hvor c er et vilkårligt reelt tal, kaldes en konstant funktionEn funktion af formen f(x)=c, hvor c er et reelt tal… Konstante funktioner er lineære og kan skrives f(x)=0x+c. I denne form er det klart, at hældningen er 0 og y-interceptet er (0,c). Evaluering af en hvilken som helst værdi for x, f.eks. x = 2, vil resultere i c.
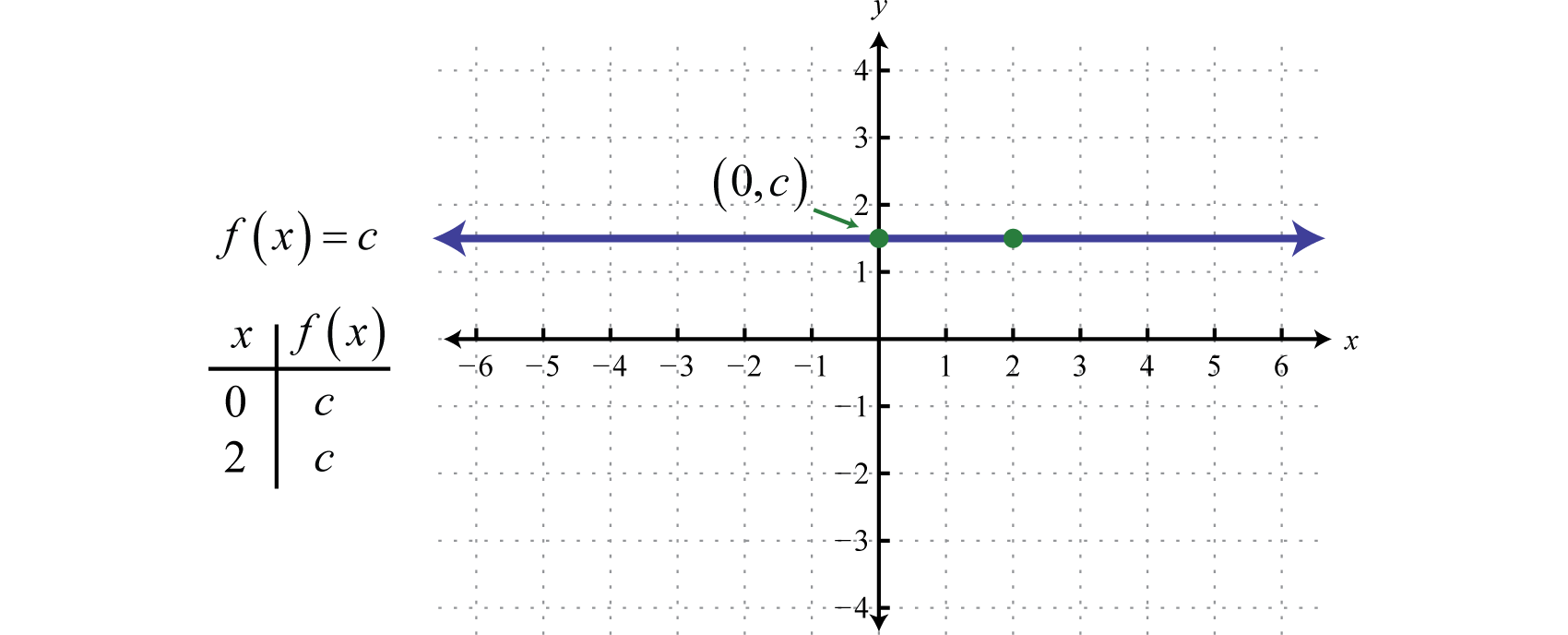
Den graf for en konstant funktion er en vandret linje. Domænet består af alle reelle tal ℝ og området består af den enkelte værdi {c}.
Dernæst definerer vi identitetsfunktionenDen lineære funktion, der er defineret ved f(x)=x. f(x)=x. Evaluering af en hvilken som helst værdi for x vil resultere i den samme værdi. F.eks. f(0)=0 og f(2)=2. Identitetsfunktionen er lineær, f(x)=1x+0, med hældning m=1 og y-intercept (0, 0).
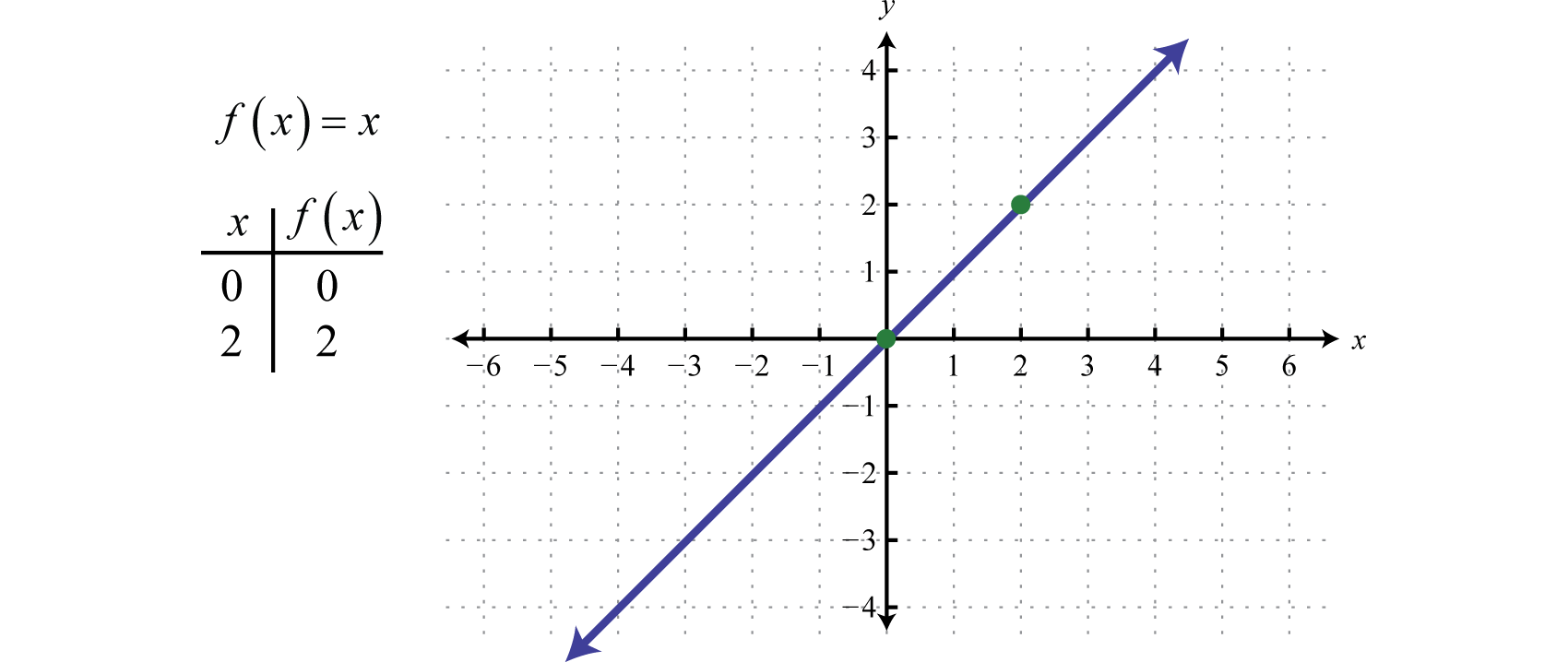
Domænet og området består begge af alle reelle tal.
Den kvadratiske funktionDen kvadratiske funktion, defineret ved f(x)=x2., defineret ved f(x)=x2, er den funktion, der fås ved at kvadrere værdierne i domænet. F.eks. er f(2)=(2)2=4 og f(-2)=(-2)2=4. Resultatet af kvadreringen af værdier, der ikke er nul i domænet, vil altid være positivt.
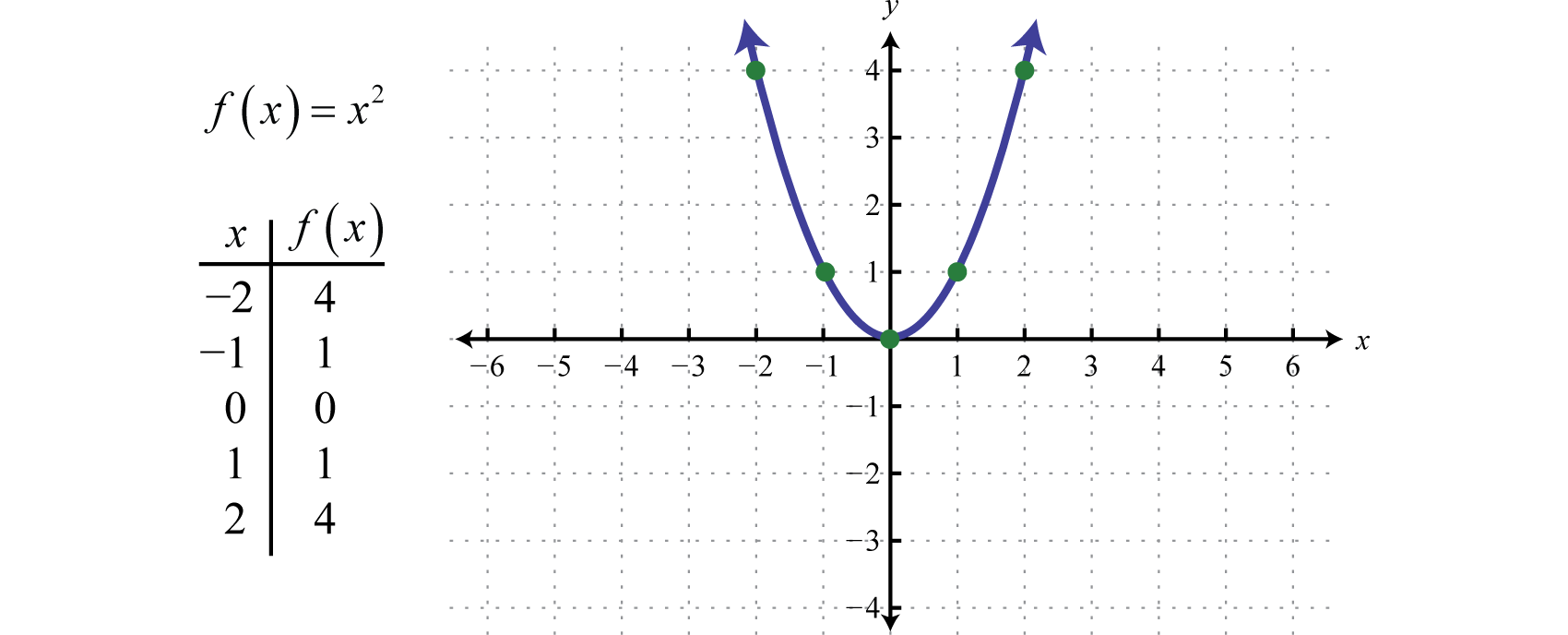
Den resulterende krumme graf kaldes en parabelDen krumme graf, der dannes af kvadreringsfunktionen… Domænet består af alle reelle tal ℝ og området består af alle y-værdier større end eller lig med nul [0,∞).
Den kubiserende funktionDen kubiske funktion, defineret ved f(x)=x3., defineret ved f(x)=x3, hæver alle værdierne i domænet til tredje potens. Resultaterne kan enten være positive, nul eller negative. F.eks. er f(1)=(1)3=1, f(0)=(0)3=0, og f(-1)=(-1)3=-1.
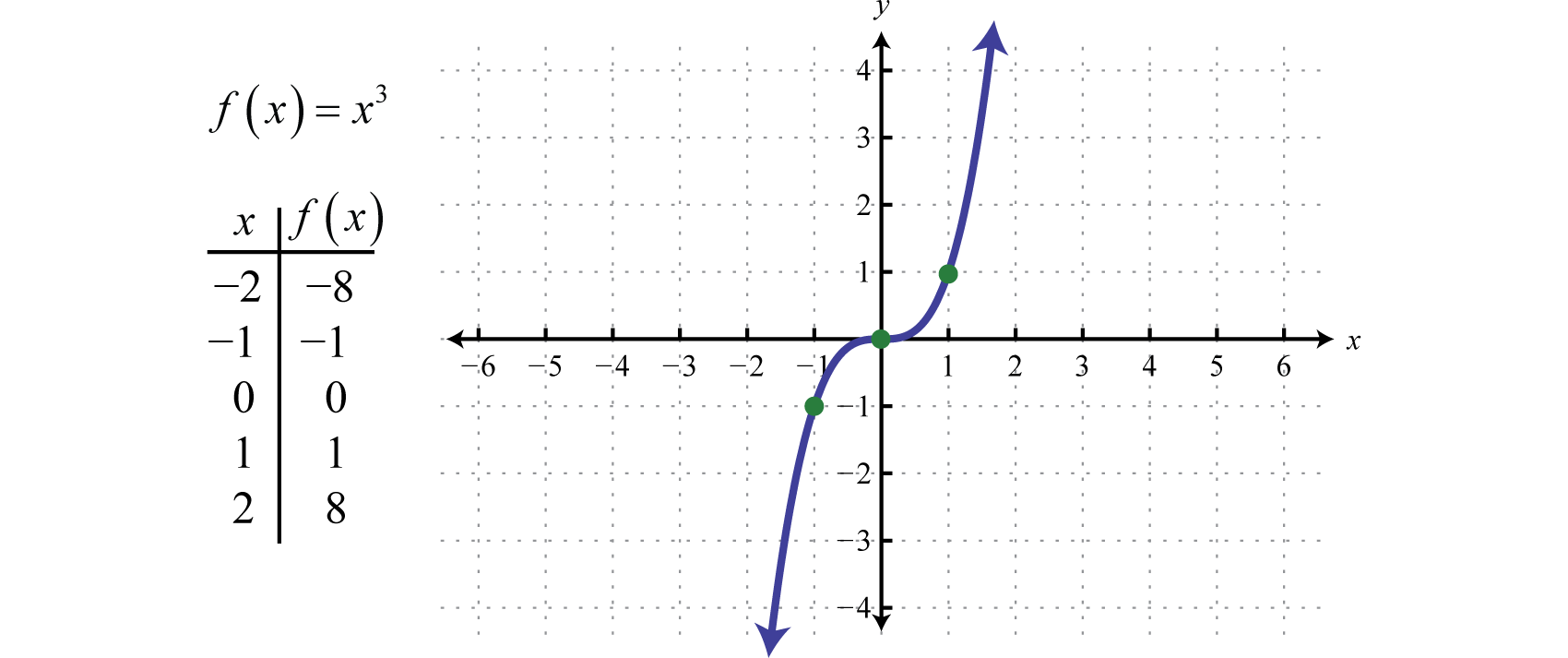
Domænet og området består begge af alle reelle tal ℝ.
Bemærk, at konstant-, identitets-, kvadrerings- og kubikfunktionen alle er eksempler på grundlæggende polynomiske funktioner. De næste tre grundfunktioner er ikke polynomier.
Den absolutte værdifunktionDen funktion, der er defineret ved f(x)=|x|., defineret ved f(x)=|x|, er en funktion, hvor output repræsenterer afstanden til oprindelsen på en tallinje. Resultatet af evalueringen af den absolutte værdifunktion for enhver værdi af x, der ikke er nul, vil altid være positivt. F.eks. er f(-2)=|-2|=2 og f(2)=|2|=2.
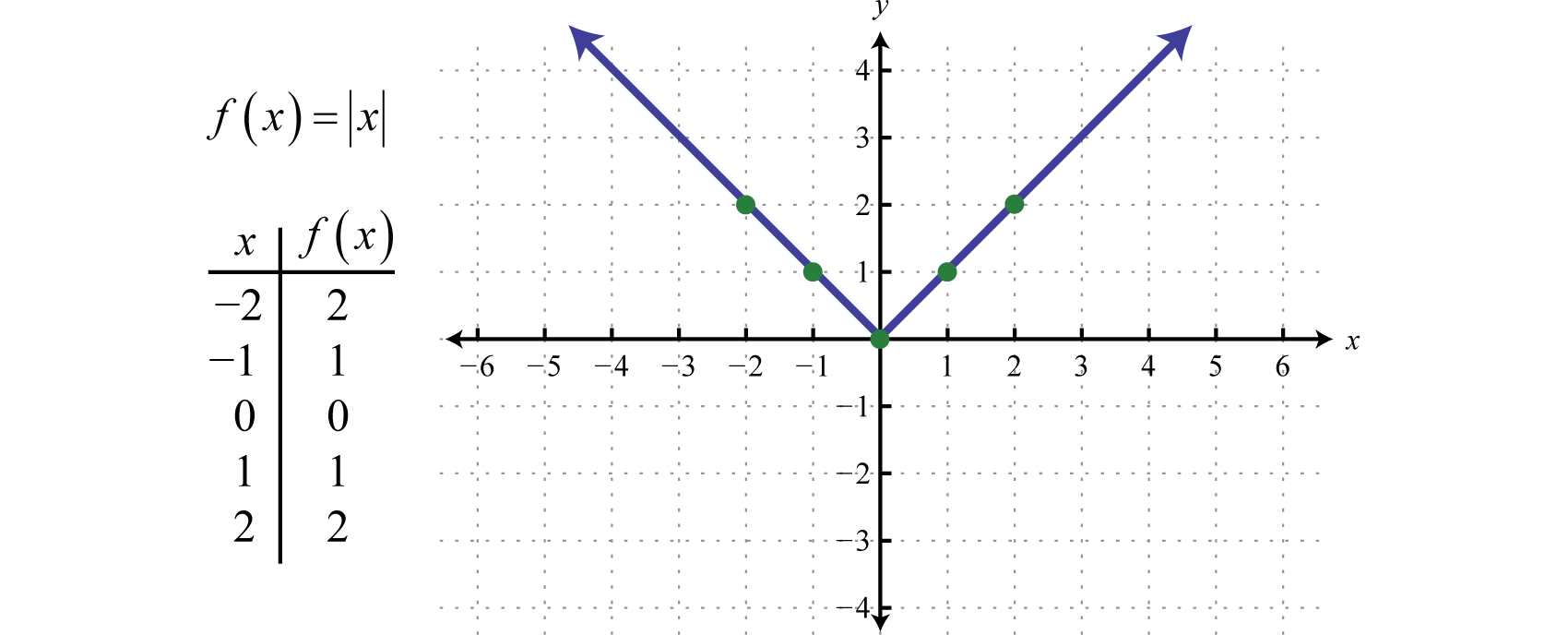
Domænet for den absolutte værdifunktion består af alle reelle tal ℝ og området består af alle y-værdier større end eller lig med nul [0,∞).
Den kvadratiske rodfunktionFunktionen, der er defineret ved f(x)=x., defineret ved f(x)=x, er ikke defineret til at være et reelt tal, hvis x-værdierne er negative. Derfor er den mindste værdi i domænet nul. F.eks. f(0)=0=0 og f(4)=4=2.
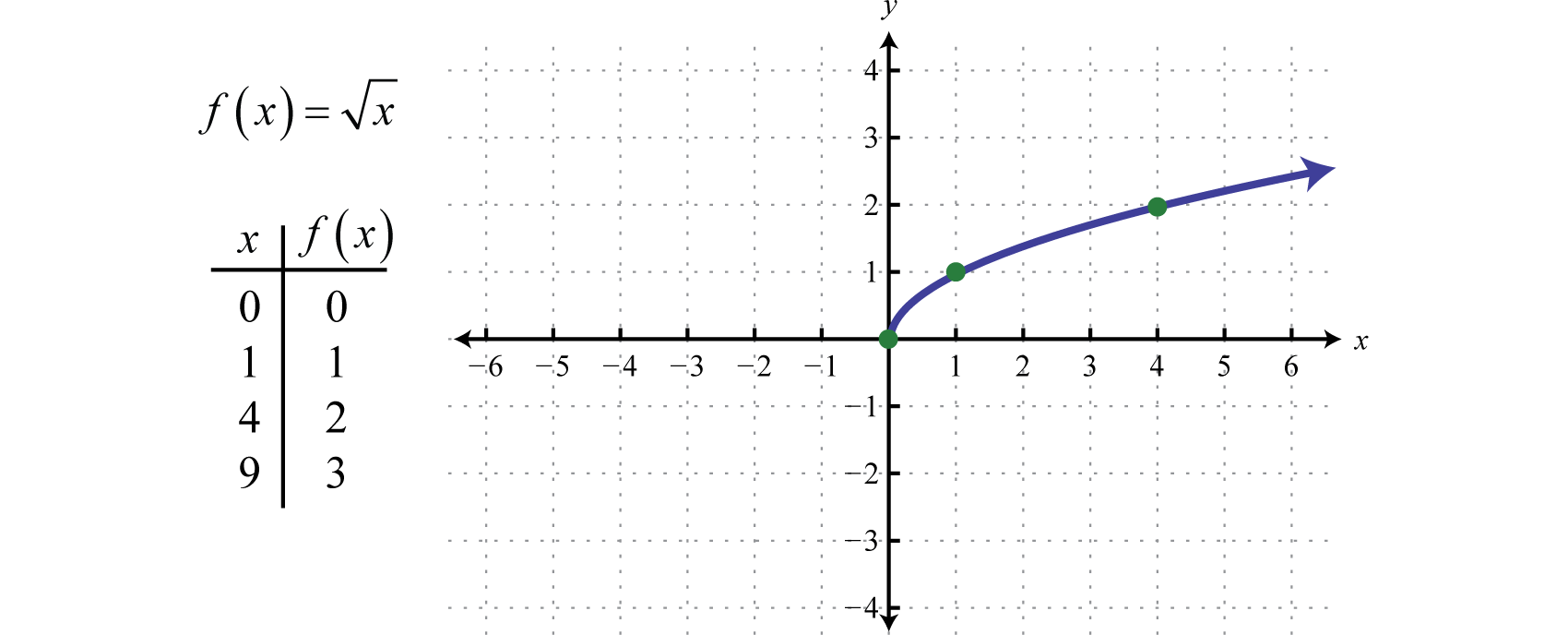
Domænet og intervallet består begge af reelle tal større end eller lig med nul [0,∞).
Den reciprokke funktionDen funktion defineret ved f(x)=1x., defineret ved f(x)=1x, er en rationel funktion med én begrænsning på domænet, nemlig x≠0. Det reciprokke af en x-værdi meget tæt på nul er meget stort. F.eks.
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1.000)=1(11.000)=1⋅1,0001=1.000
Med andre ord vil deres reciprokale værdier, efterhånden som x-værdierne nærmer sig nul, have en tendens mod enten positiv eller negativ uendelighed. Dette beskriver en lodret asymptoteEn lodret linje, som en graf kommer uendeligt tæt på. på y-aksen. Når x-værdierne er meget store, er resultatet af den reciprokke funktion desuden meget lille.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11.000=0,001
Med andre ord, når x-værdierne bliver meget store, tenderer de resulterende y-værdier mod nul. Dette beskriver en horisontal asymptoteEn horisontal linje, som en graf bliver uendeligt tæt på, hvor x-værdierne tenderer mod ±∞. på x-aksen. Efter at have plottet et antal punkter kan den reciprokke funktions generelle form bestemmes.
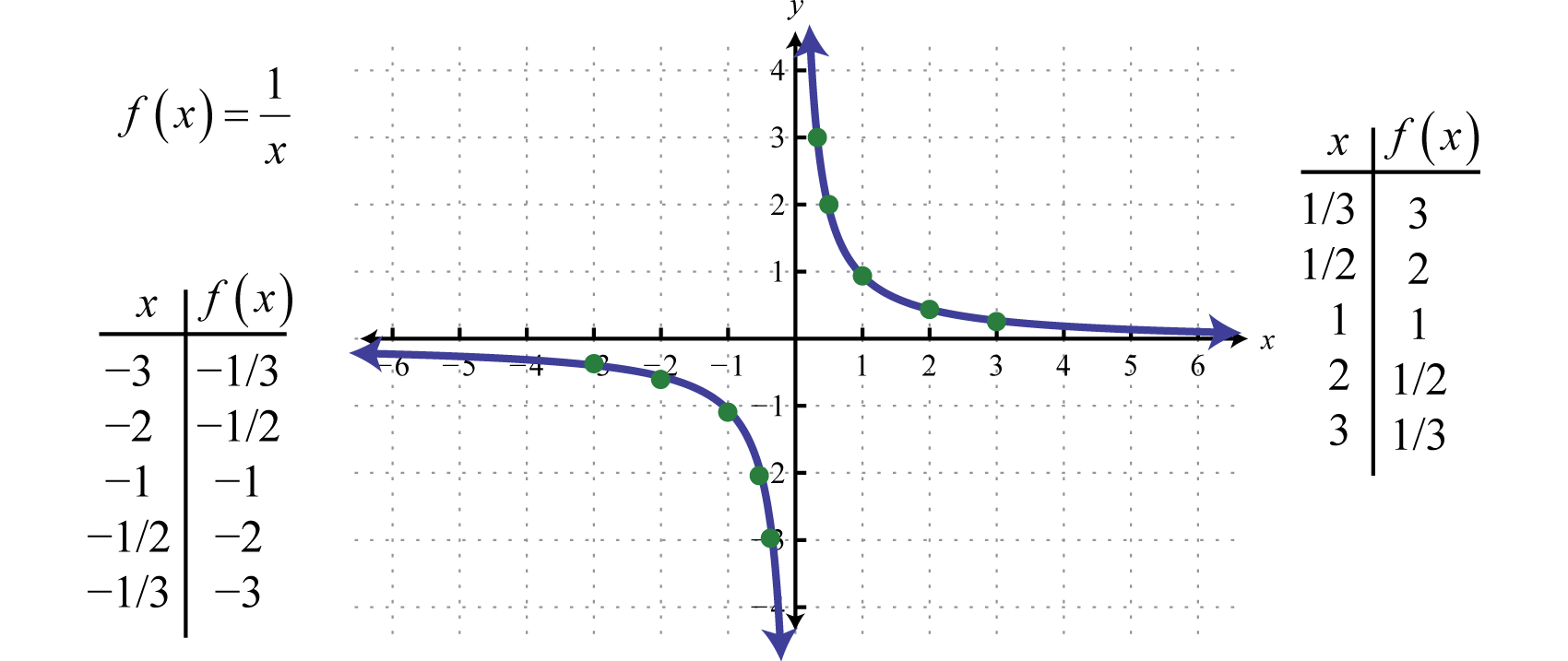
Både den reciprokke funktions domæne og område består af alle reelle tal undtagen 0, som kan udtrykkes ved hjælp af intervalnotation på følgende måde: (-∞,0)∪(0,∞).
