Základní funkce
V této části si vykreslíme sedm základních funkcí, které budeme používat v průběhu celého kurzu. Každá funkce se graficky znázorní vynesením bodů. Nezapomeňte, že f(x)=y, a proto lze f(x) a y používat zaměnitelně.
Každá funkce tvaru f(x)=c, kde c je libovolné reálné číslo, se nazývá konstantní funkceKaždá funkce tvaru f(x)=c, kde c je reálné číslo, se nazývá konstantní funkce a.. Konstantní funkce jsou lineární a lze je zapsat f(x)=0x+c. V tomto tvaru je zřejmé, že sklon je 0 a průsečík y je (0,c). Vyhodnocením libovolné hodnoty pro x, například x = 2, získáme c.
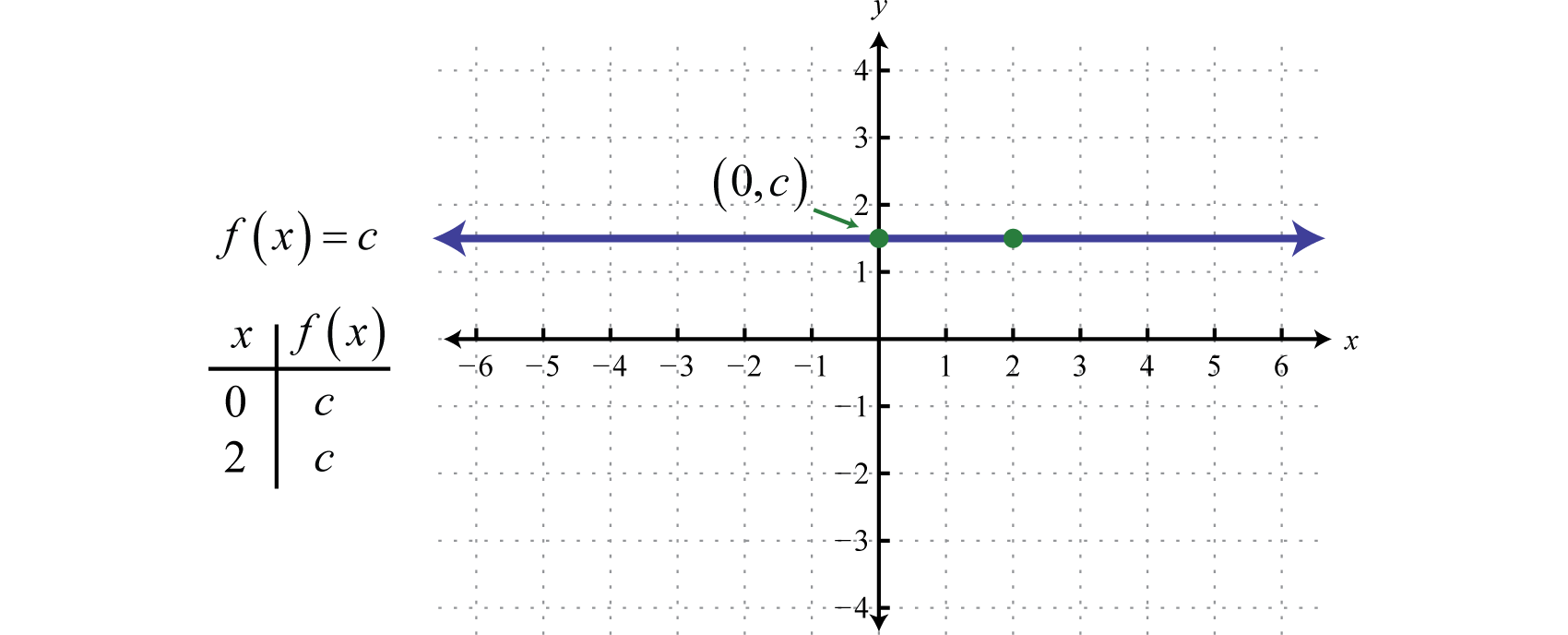
Grafem konstantní funkce je vodorovná přímka. Obor tvoří všechna reálná čísla ℝ a obor tvoří jediná hodnota {c}.
Dále definujeme funkci identityLineární funkce definovaná vztahem f(x)=x. f(x)=x. Vyhodnocením libovolné hodnoty pro x získáme stejnou hodnotu. Například f(0)=0 a f(2)=2. Funkce identity je lineární, f(x)=1x+0, se sklonem m=1 a průsečíkem y (0, 0).
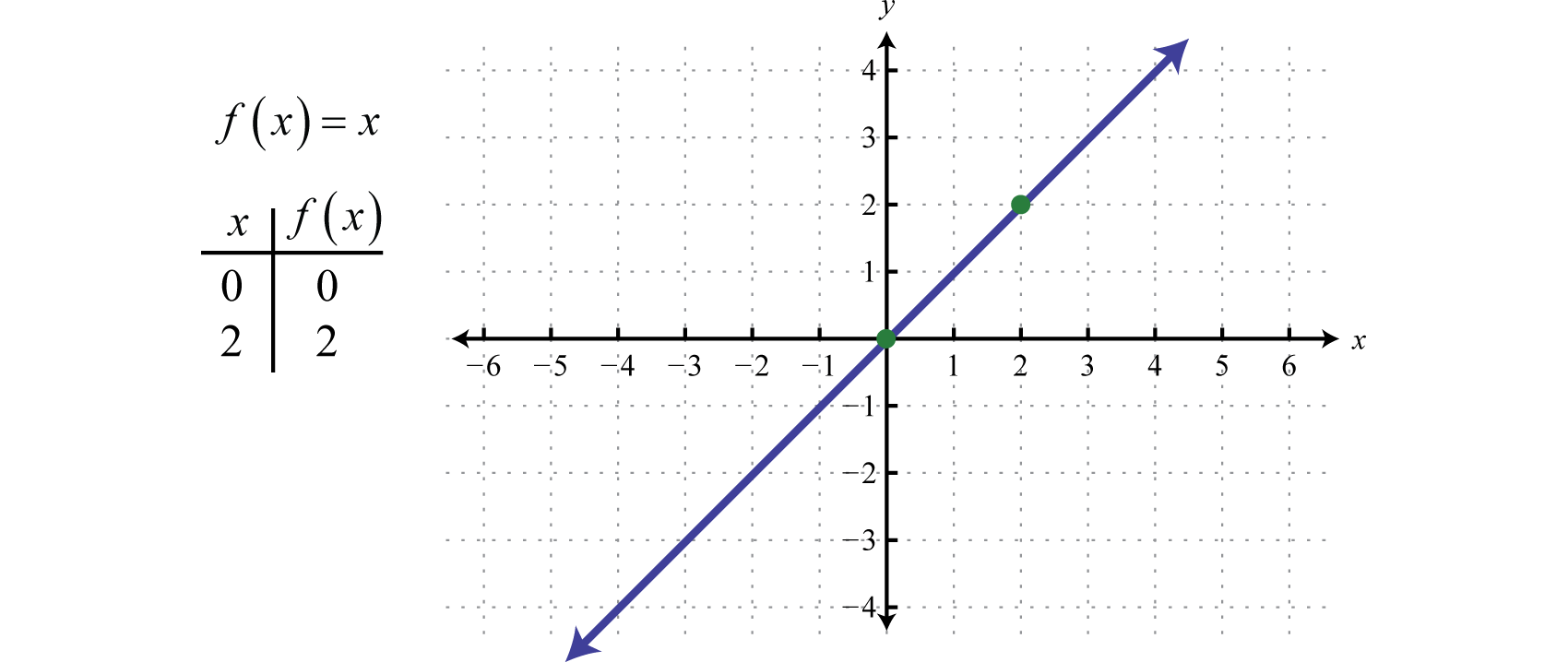
Oblast i rozsah tvoří všechna reálná čísla.
Kvadratická funkceKvadratická funkce definovaná f(x)=x2., definovaná f(x)=x2, je funkce získaná odmocněním hodnot v oboru. Například f(2)=(2)2=4 a f(-2)=(-2)2=4. Výsledek odmocnění nenulových hodnot v oboru bude vždy kladný.
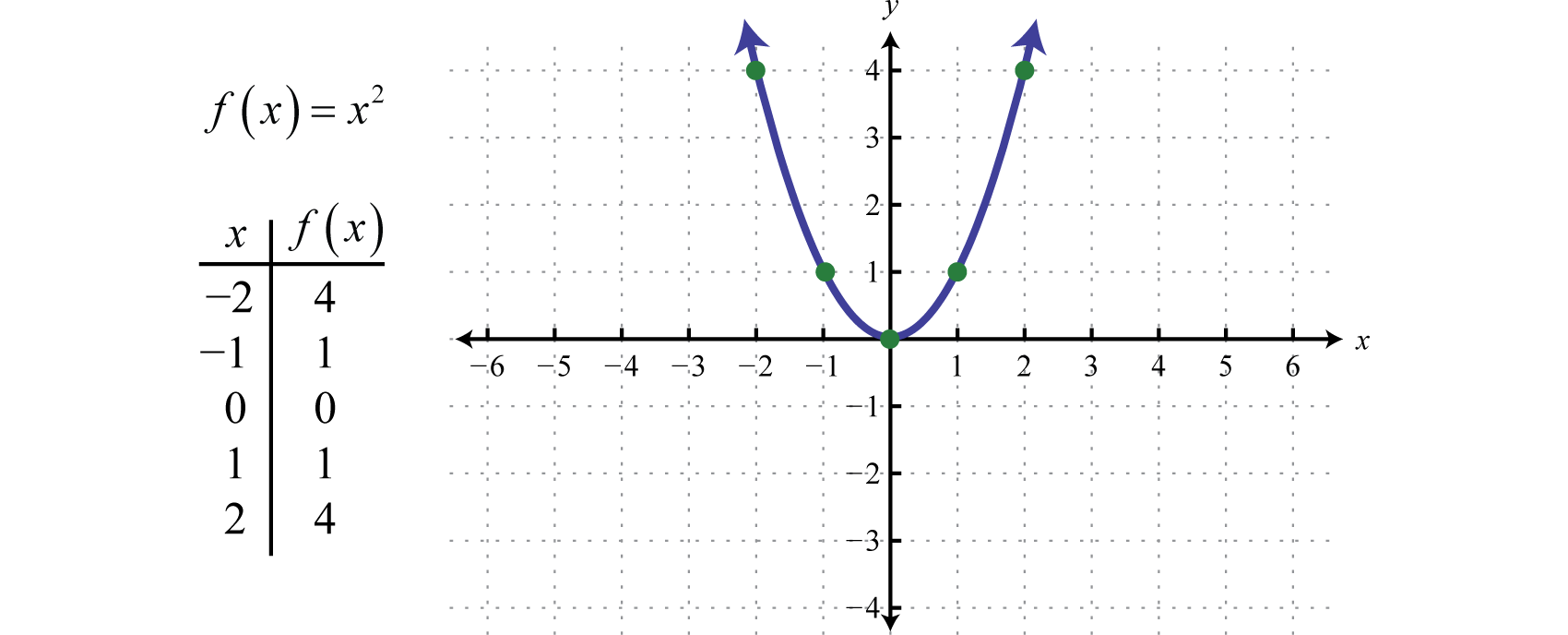
Výsledný zakřivený graf se nazývá parabolaZakřivený graf vzniklý odmocněním funkce se nazývá parabola. Obor tvoří všechna reálná čísla ℝ a obor tvoří všechny hodnoty y větší nebo rovné nule [0,∞).
Kubovací funkceKubovací funkce definovaná f(x)=x3. definovaná f(x)=x3, zvyšuje všechny hodnoty v oboru na třetí mocninu. Výsledek může být buď kladný, nulový, nebo záporný. Například f(1)=(1)3=1, f(0)=(0)3=0 a f(-1)=(-1)3=-1.
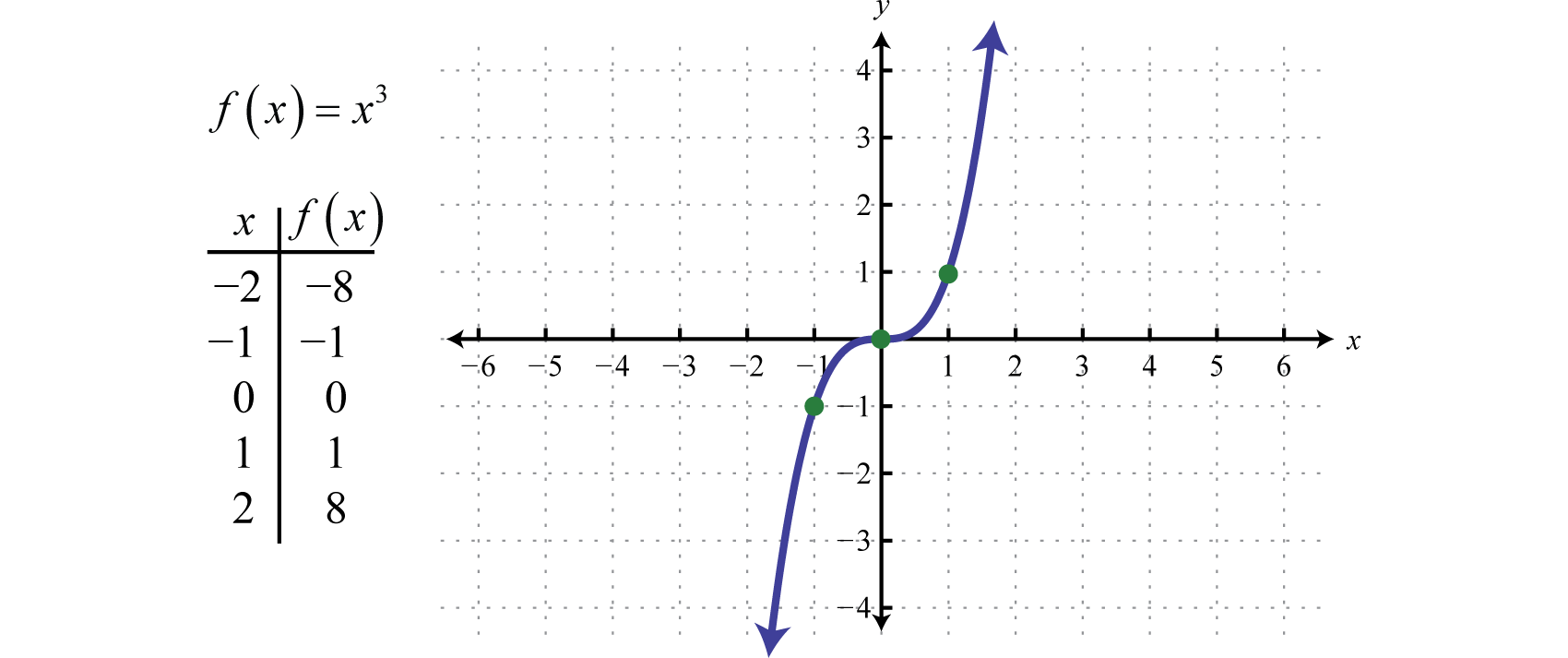
Oblast i rozsah tvoří všechna reálná čísla ℝ.
Všimněte si, že funkce konstanty, identity, odmocňování a kubizace jsou příklady základních polynomů. Další tři základní funkce nejsou polynomy.
Funkce absolutní hodnotyFunkce definovaná f(x)=|x|., definovaná f(x)=|x|, je funkce, jejíž výstup představuje vzdálenost od počátku na číselné přímce. Výsledek vyhodnocení funkce absolutní hodnoty pro libovolnou nenulovou hodnotu x bude vždy kladný. Například f(-2)=|-2|=2 a f(2)=|2|=2.
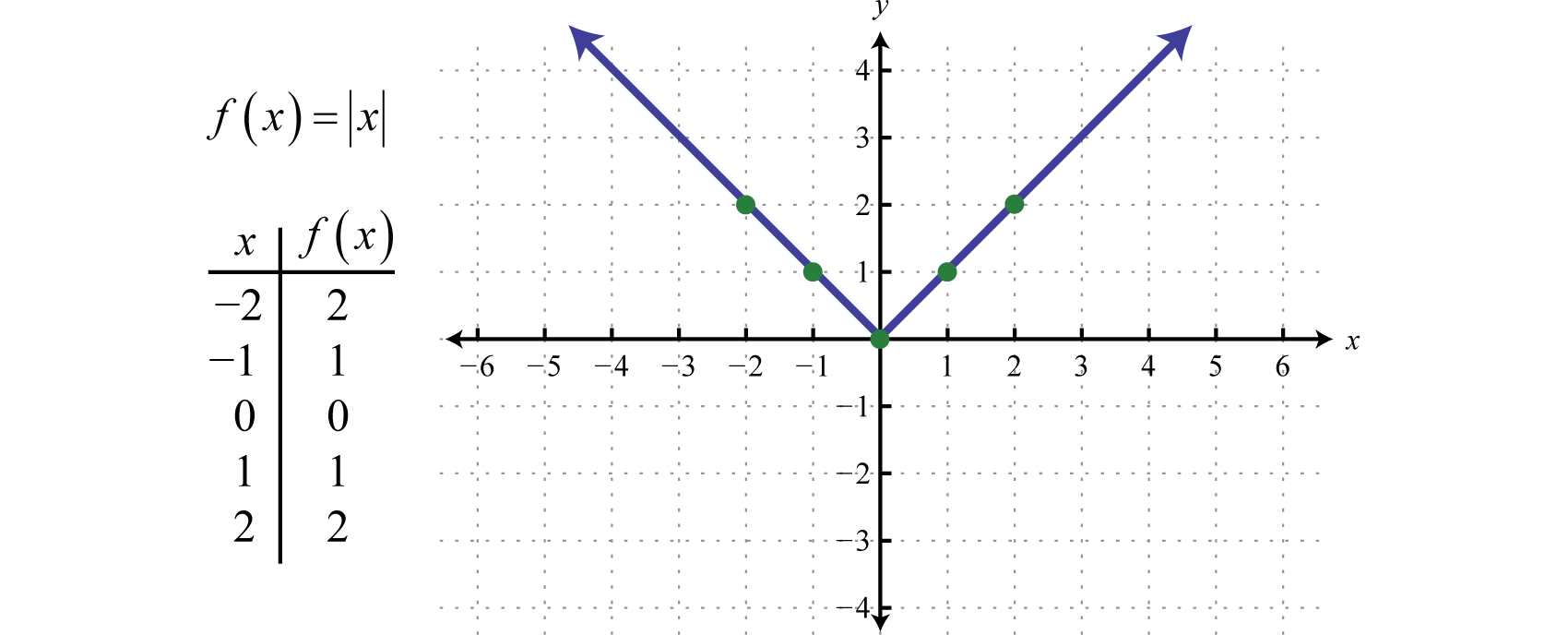
Oblast funkce absolutní hodnoty tvoří všechna reálná čísla ℝ a obor tvoří všechny hodnoty y větší nebo rovné nule [0,∞).
Funkce odmocninyFunkce definovaná vztahem f(x)=x., definovaná pomocí f(x)=x, není definována jako reálné číslo, pokud jsou hodnoty x záporné. Nejmenší hodnota v oboru je tedy nula. Například f(0)=0=0 a f(4)=4=2.
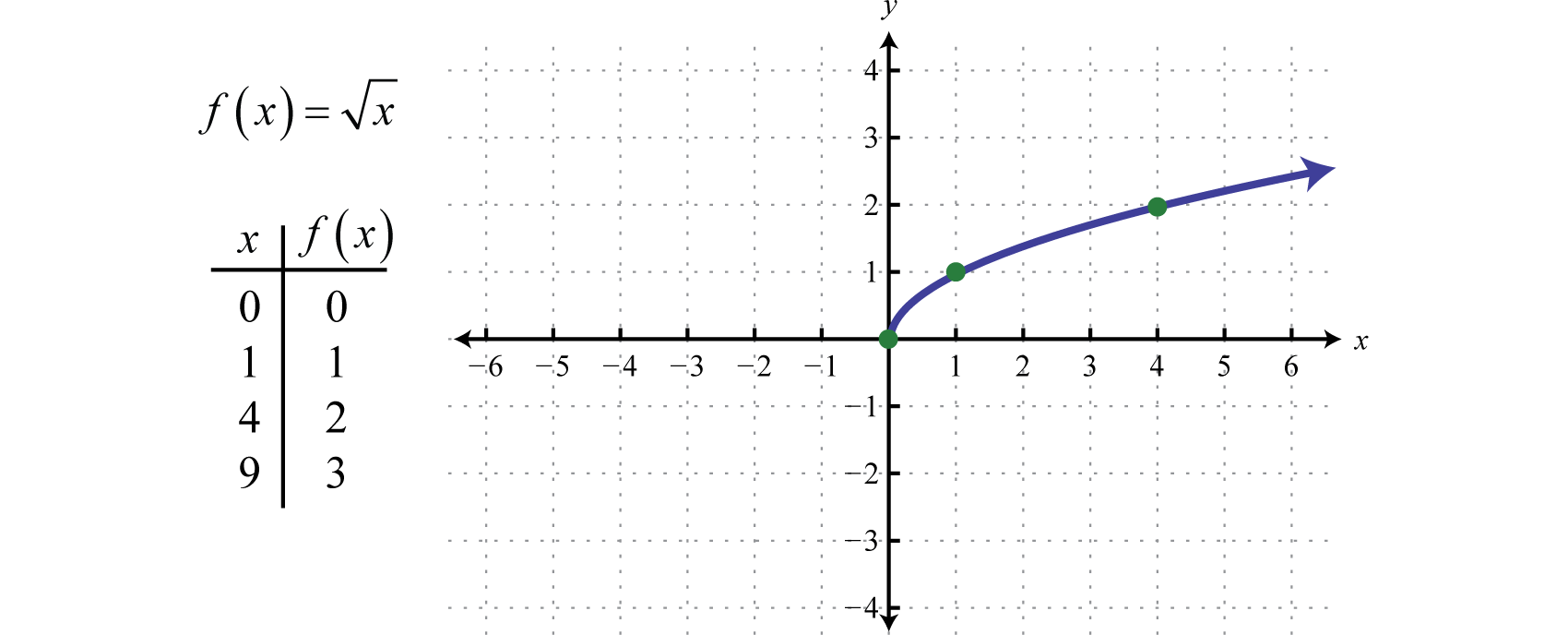
Oblast i obor se skládají z reálných čísel větších nebo rovných nule [0,∞).
Reciproční funkceFunkce definovaná f(x)=1x., definovaná f(x)=1x, je racionální funkce s jedním omezením na oblast, a to x≠0. Funkce f(x)=1x, definovaná f(x)=1x, je racionální funkce s jedním omezením na oblast. Reciproční hodnota x velmi blízká nule je velmi velká. Například,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1 000)=1(11 000)=1⋅1 0001=1 000
Jinými slovy, jak se hodnoty x blíží nule, jejich reciproké hodnoty budou směřovat buď ke kladnému, nebo zápornému nekonečnu. To popisuje svislou asymptotuSvislá čára, ke které se graf nekonečně přibližuje. na ose y. Navíc tam, kde jsou hodnoty x velmi velké, je výsledek reciproké funkce velmi malý.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11 000=0,001
Jinými slovy, jakmile jsou hodnoty x velmi velké, výsledné hodnoty y směřují k nule. To popisuje horizontální asymptotuVodorovná čára, ke které se graf nekonečně přibližuje, když hodnoty x směřují k ±∞. na ose x. Po vynesení řady bodů lze určit obecný tvar reciproké funkce.
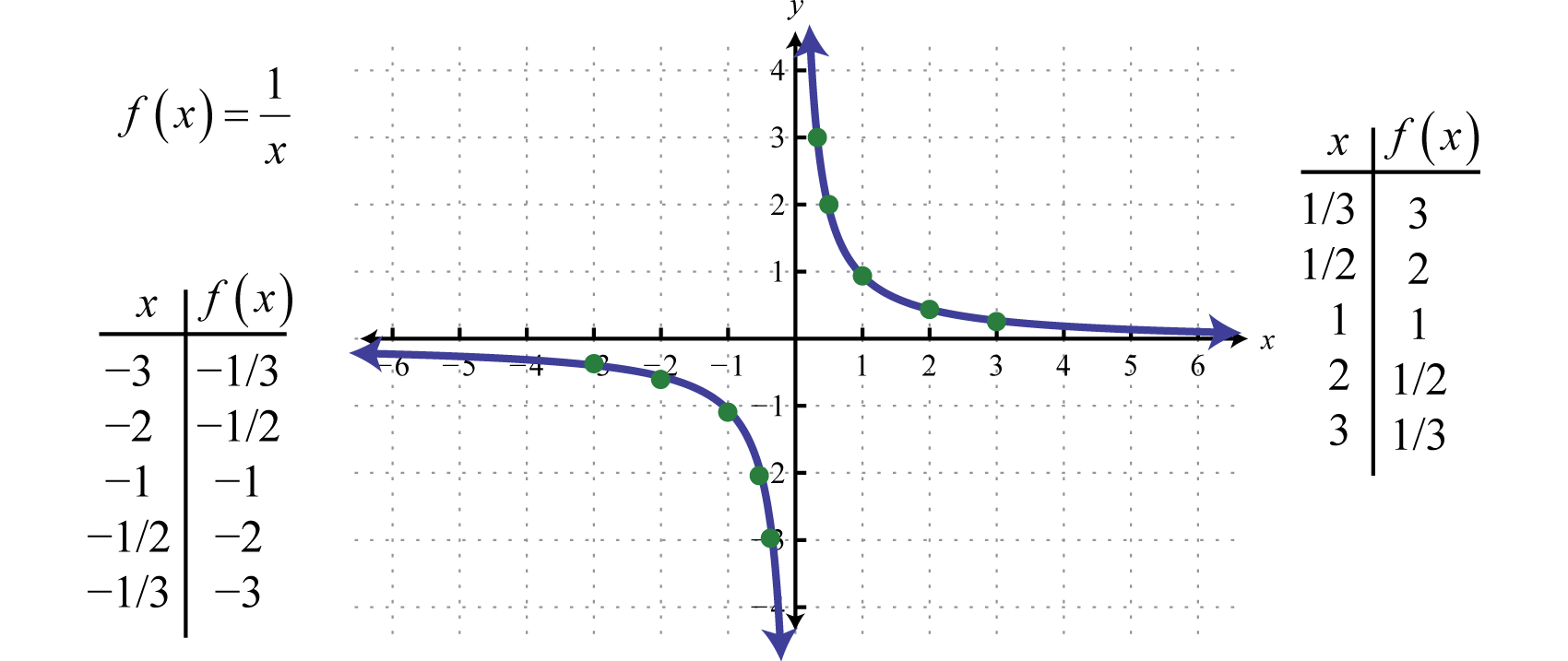
Oblast i obor reciproké funkce tvoří všechna reálná čísla kromě 0, což lze vyjádřit pomocí intervalového zápisu takto: (-∞,0)∪(0,∞).
