Wald-test: Definition, exempel, hur man utför testet

Hypotesprövning > Wald-test

Vad är Wald-testet?

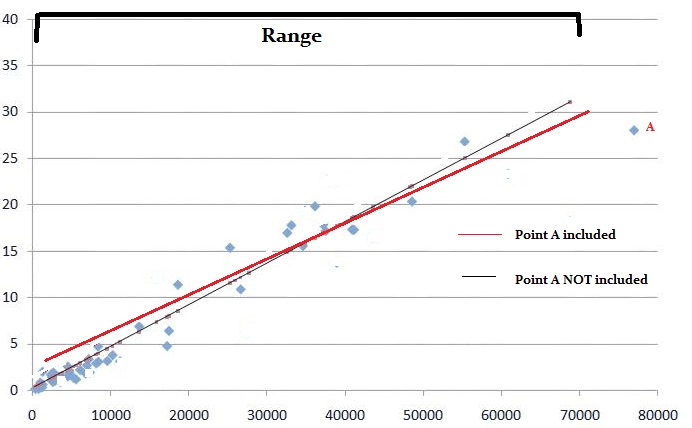
Wald-testet kan tala om för dig vilka modellvariabler som bidrar med något signifikant.

Wald-testet (även kallat Wald Chi-Squared Test) är ett sätt att ta reda på om förklarande variabler i en modell är signifikanta. ”Signifikant” betyder att de bidrar med något till modellen; variabler som inte bidrar med något kan tas bort utan att påverka modellen på något meningsfullt sätt. Testet kan användas för en mängd olika modeller, inklusive modeller med binära variabler eller kontinuerliga variabler.
Nollhypotesen för testet är: någon parameter = något värde. Du kanske till exempel studerar om vikten påverkas av att äta skräpmat två gånger i veckan. ”Vikt” skulle vara din parameter. Värdet kan vara noll (vilket indikerar att du inte tror att vikten påverkas av att äta skräpmat). Om nollhypotesen förkastas tyder det på att variablerna i fråga kan tas bort utan större skada för modellens passform.

• Om Wald-testet visar att parametrarna för vissa förklarande variabler är noll kan du ta bort variablerna från modellen.
• Om testet visar att parametrarna inte är noll bör du inkludera variablerna i modellen.

Vald-testet brukar man tala om i termer av chi-kvadrat, eftersom provtagningsfördelningen (när n närmar sig oändligheten) vanligtvis är känd. Denna variant av testet kallas ibland Wald Chi-Squared Test för att skilja det från Wald Log-Linear Chi-Square Test, som är en icke-parametrisk variant baserad på log odds ratios.

Bjämförelse med andra test

Wald-testet är en grov approximation av Likelihood Ratio Test. Du kan dock köra det med en enda modell (LR-testet kräver minst två). Det är också mer allmänt tillämpbart än LRT: ofta kan man köra ett Wald-test i situationer där inget annat test kan köras.

För stora värden på n är Wald-testet ungefär likvärdigt med t-testet; båda testerna förkastar samma värden för stora urvalsstorlekar. Wald-, LRT- och Lagrange-multiplikatortestet är alla likvärdiga när provstorlekarna närmar sig oändligheten (kallas ”asymptotiskt likvärdiga”). Urval av ändlig storlek, särskilt mindre urval, kommer dock sannolikt att ge mycket olika resultat.

Agresti (1990) föreslår att du bör använda LRT i stället för Wald-testet för små urvalsstorlekar eller om parametrarna är stora. En ”liten” provstorlek är mindre än 30.

Körning av testet

Behövs hjälp med en läxfråga? Kolla in vår handledningssida!

Formeln för statistiken för Wald-testet är: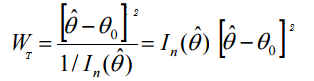

Varvid:

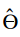• = Maximum Likelihood Estimator (MLE),
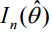• = förväntad Fisher-information (utvärderad vid MLE).

Testet letar i princip efter skillnader: Θ0 – Θ. De allmänna stegen är:

1. Hitta MLE.
2. Hitta den förväntade Fisher-informationen.
3. Utvärdera Fisher-informationen vid MLE.

Med kombinationen av MLE- och Fisher-informationen är Wald-testet mycket komplext att arbeta med och brukar inte beräknas för hand. Många programvaror kan köra testet.

• Stata: använd kommandot test.
• R: se WALD-testinstruktioner för R (laddar ner en PDF) från University of Toronto.
• SAS: Använd TEST-kommandot. WALD är standard om inget test anges.

Reference:
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.

——————————————————————————

Har du behov av hjälp med en läxa eller en provfråga? Med Chegg Study kan du få steg-för-steg-lösningar på dina frågor från en expert inom området. Dina första 30 minuter med en Chegg-handledare är gratis!