
Pythagoras av Samos (ca.570-495 BCE)
Biografi – Vem var Pythagoras
Det hävdas ibland att vi har Pythagoras att tacka för den rena matematiken, och han kallas ofta för den första ”sanna” matematikern. Men även om hans bidrag uppenbarligen var viktigt förblir han ändå en kontroversiell person.
Han lämnade själv inga matematiska skrifter efter sig, och mycket av det vi vet om det pythagoreiska tänkandet kommer till oss från Philolaus’ och andra senare pythagoreiska lärdas skrifter. Det är faktiskt inte alls klart om många (eller ens några) av de satser som tillskrivs honom faktiskt löstes av Pythagoras personligen eller av hans anhängare.
Skolan som han grundade i Croton i södra Italien omkring 530 f.v.t. var kärnan i en ganska bisarr pythagoreisk sekt. Även om det pythagoreiska tänkandet till stor del dominerades av matematik var det också djupt mystiskt, och Pythagoras införde sina kvasireligiösa filosofier, sin strikta vegetarism, sitt gemensamma liv, sina hemliga riter och sina märkliga regler för alla medlemmar i sin skola (inklusive bisarra och till synes slumpmässiga påbud om att man aldrig får urinera mot solen, att man aldrig får gifta sig med en kvinna som bär guldsmycken, att man aldrig får gå förbi en åsna som ligger på gatan, att man aldrig får äta eller ens röra vid svarta favabönor, etc.) .
Medlemmarna delades upp i ”mathematikoi” (eller ”lärarna”), som utökade och utvecklade det mer matematiska och vetenskapliga arbete som Pythagoras själv påbörjade, och ”akousmatikoi” (eller ”lyssnarna”), som fokuserade på de mer religiösa och rituella aspekterna av hans läror. Det fanns alltid ett visst mått av friktion mellan de två grupperna och så småningom blev sekten indragen i några häftiga lokala strider och upplöstes slutligen. Det byggdes upp ett missnöje mot pythagoréernas hemlighetsmakeri och exklusivitet, och 460 f.Kr. brändes och förstördes alla deras mötesplatser, och minst 50 medlemmar dödades bara i Croton.
Den övergripande devisen i Pythagoras skola var ”Allt är tal” eller ”Gud är tal”, och pythagoréerna praktiserade i själva verket ett slags numerologi eller taldyrkan, och ansåg att varje tal hade sin egen karaktär och betydelse. Till exempel var talet ett generatorn för alla tal; två representerade åsikt; tre, harmoni; fyra, rättvisa; fem, äktenskap; sex, skapelse; sju, de sju planeterna eller ”vandrande stjärnorna”; osv. Udda tal betraktades som kvinnliga och jämna tal som manliga.
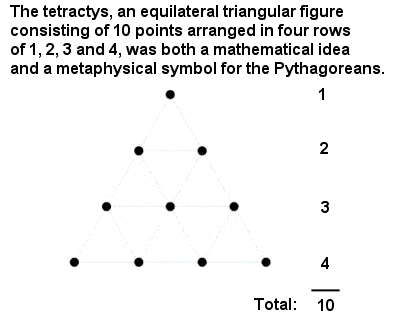
Den pythagoreiska Tetractys
Det heligaste talet av alla var ”Tetractys” eller tio, ett triangulärt tal som består av summan av ett, två, tre och fyra. Det är en stor hyllning till pythagoréernas intellektuella prestationer att de härledde talets särskilda plats till talet 10 från ett abstrakt matematiskt argument snarare än från något så vardagligt som att räkna fingrarna på två händer.
Pythagoras och hans skola – liksom en handfull andra matematiker i det antika Grekland – var dock till stor del ansvariga för att införa en strängare matematik än vad som hade funnits tidigare, som byggde på första principer med hjälp av axiom och logik. Före Pythagoras hade till exempel geometrin endast varit en samling regler som härletts genom empiriska mätningar.
Pythagoras upptäckte att det gick att konstruera ett komplett matematiskt system där geometriska element motsvarade tal och där heltal och deras förhållanden var allt som krävdes för att upprätta ett helt system av logik och sanning.
Pythagoras sats
Han är främst ihågkommen för det som blivit känt som Pythagoras sats (eller Pythagoras sats): att för varje rätvinklig triangel är kvadraten på längden av hypotenusan (den längsta sidan, mittemot den räta vinkeln) lika med summan av kvadraten på de andra två sidorna (eller ”benen”).
Skrivet som en ekvation: a2 + b2 = c2.
Vad Pythagoras och hans anhängare inte insåg är att detta också fungerar för vilken form som helst: således är arean av en femhörning på hypotenusan lika med summan av femhörningarna på de andra två sidorna, precis som för en halvcirkel eller någon annan regelbunden (eller till och med oregelbunden( form.
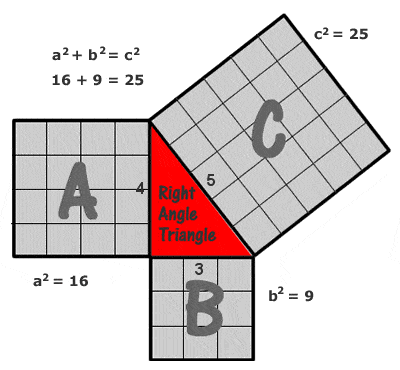
Pythagoras (Pythagoras) sats
Det enklaste och mest citerade exemplet på en Pythagoras triangel är en triangel med sidorna 3, 4 och 5 enheter (32 + 42 = 52, vilket kan ses genom att rita ett rutnät av enhetsrutor på varje sida som i diagrammet till höger), men det finns ett potentiellt oändligt antal andra heltaliga ”pythagoriska tripplar”, som börjar med (5, 12, 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), osv. Det bör dock noteras att (6, 8, 10) inte är vad som kallas en ”primitiv” pythagorisk trippel, eftersom den bara är en multipel av (3, 4, 5).
Pythagoras sats och egenskaperna hos rätvinkliga trianglar tycks vara den äldsta och mest utbredda matematiska utvecklingen efter den grundläggande aritmetiken och geometrin och den berördes i några av de äldsta matematiska texterna från Babylon och Egypten, som härrör från över tusen år tidigare. Ett av de enklaste bevisen kommer från det gamla Kina och är troligen från långt före Pythagoras födelse. Det var dock Pythagoras som gav satsen dess slutgiltiga form, även om det inte är klart om Pythagoras själv slutgiltigt bevisade den eller bara beskrev den. Hur som helst har det blivit en av de mest kända matematiska satserna, och det finns nu så många som 400 olika bevis, en del geometriska, en del algebraiska, en del med hjälp av avancerade differentialekvationer, etc.
Det blev dock snart uppenbart att det också var möjligt med icke heltalslösningar, så att en likbent triangel med sidorna 1, 1 och √2, till exempel, också har en rätvinklig vinkel, vilket babylonierna hade upptäckt flera århundraden tidigare. När Pythagoras’ elev Hippasus försökte beräkna värdet av √2 fann han dock att det inte gick att uttrycka det som en bråkdel, vilket visade på den potentiella existensen av en helt ny värld av tal, de irrationella talen (tal som inte kan uttryckas som enkla bråkdelar av heltal). Denna upptäckt krossade ganska mycket den eleganta matematiska värld som Pythagoras och hans anhängare hade byggt upp, och existensen av ett tal som inte kunde uttryckas som kvoten mellan två av Guds skapelser (vilket är hur de tänkte sig heltalen) äventyrade hela sektens trossystem.
Den stackars Hippasus dränktes tydligen av de hemlighetsfulla pythagoréerna för att han hade spridit denna viktiga upptäckt till omvärlden. Men att ersätta idén om helheternas gudomlighet med det rikare begreppet kontinuum var en viktig utveckling inom matematiken. Det markerade den grekiska geometrins verkliga födelse, som handlar om linjer, plan och vinklar, som alla är kontinuerliga och inte diskreta.
Enligt sina andra prestationer inom geometrin insåg Pythagoras (eller åtminstone hans efterföljare, pythagoréerna) också att summan av vinklarna i en triangel är lika med två rätvinkliga vinklar (180°), och troligen också den generalisering som säger att summan av de inre vinklarna i en polygon med n sidor är lika med (2n – 4) rätvinkliga vinklar, och att summan av de yttre vinklarna är lika med 4 rätvinkliga vinklar. De kunde konstruera figurer med en given area och använda enkel geometrisk algebra, till exempel lösa ekvationer som a(a – x) = x2 med geometriska medel.
Pythagoréerna lade också grunden för talteori, med sina undersökningar av triangulära, kvadratiska och även perfekta tal (tal som är summan av sina divisorer). De upptäckte flera nya egenskaper hos kvadratiska tal, t.ex. att kvadraten på ett tal n är lika med summan av de första n udda talen (t.ex. 42 = 16 = 1 + 3 + 5 + 7). De upptäckte också åtminstone det första paret av amicabla tal, 220 och 284 (amicabla tal är talpar för vilka summan av divisorerna i det ena talet är lika med det andra talet, t.ex. är de egentliga divisorerna i 220 1, 2, 4, 4, 5, 10, 11, 20, 22, 44, 55 och 110, varav summan är 284, och de egentliga divisorerna i 284 är 1, 2, 4, 71 och 142, varav summan är 220).
Musikteori
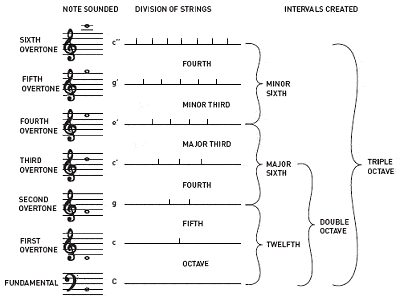
Pythagoras tillskrivs upptäckten av förhållandet mellan harmoniska musikaliska toner
Pythagoras tillskrivs också upptäckten att intervallen mellan harmoniska musikaliska toner alltid har hela tals förhållande. Om man till exempel spelar en halv längd på en gitarrsträng ger det samma ton som den öppna strängen, men en oktav högre; en tredjedels längd ger en annan men harmonisk ton; osv.
Nej helhetsförhållanden tenderar å andra sidan att ge dissonanta klanger. På detta sätt beskrev Pythagoras de fyra första övertonerna som skapar de gemensamma intervall som har blivit de primära byggstenarna i musikalisk harmoni: oktaven (1:1), den perfekta kvinten (3:2), den perfekta fjärdedelen (4:3) och den stora tertialen (5:4). Det äldsta sättet att stämma den kromatiska skalan med 12 toner är känt som den pythagoriska stämningen, och den bygger på en stapel perfekta kvinter, var och en stämd i förhållandet 3:2.
Den mystiske Pythagoras blev så upphetsad av denna upptäckt att han blev övertygad om att hela universum byggde på siffror och att planeterna och stjärnorna rörde sig enligt matematiska ekvationer som motsvarade musikaliska toner, och på så sätt producerade han ett slags symfoni, den ”Musical Universalis” eller ”Spheres of the Music”.
| << Tillbaka till grekisk matematik | Framåt till Platon >> |
.
