I det här avsnittet kommer vi att bekanta oss med mängdoperationer och notationer, så att vi kan tillämpa dessa begrepp på både räkne- och sannolikhetsproblem. Vi börjar med att definiera några termer.
En mängd är en samling objekt, och dess medlemmar kallas för mängdens element. Vi benämner mängden genom att använda stora bokstäver och omsluter dess medlemmar i svängda parenteser. Anta att vi behöver lista medlemmarna i schackklubben. Vi använder följande mängdnotation:
C ={Ken, Bob, Tran, Shanti, Eric}
En mängd som inte har några medlemmar kallas en tom mängd. Den tomma mängden betecknas med symbolen Ø.
Två mängder är lika om de har samma element.
En mängd A är en delmängd av en mängd B om varje medlem i A också är medlem i B.
Antag att C = {Al, Bob, Chris, David, Ed} och A = {Bob, David}. Då är A en delmängd av C, skriven som 
.
Varje mängd är en delmängd av sig själv, och den tomma mängden är en delmängd av varje mängd.
Union Of Two Sets
Låtsas A och B vara två mängder, så är unionen av A och B, skriven som 
, mängden av alla element som antingen ingår i A eller i B, eller i både A och B.
Intersektion av två mängder
Låt A och B vara två mängder, då är intersektionen av A och B, skriven som 
, mängden av alla element som är gemensamma för båda mängderna A och B.
En universell mängd U är den mängd som består av alla element under övervägande.
Komplement till en mängd
Låt A vara vilken mängd som helst, då är komplementet till mängden A, skrivet som 
, den mängd som består av element i den universella mängden U som inte finns i A.
Disjoint Sets
Två mängder A och B kallas disjoint sets om deras skärningspunkt är en tom mängd.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {orange, grönt, indigo, violett}För att uppnå en bättre förståelse kan vi anta att den universella mängden U representerar spektralfärgerna och P de primära färgerna, då representerar de spektralfärger som inte är primära färger.
.
= {röd, gul, blå, grön}
= {orange, indigo, violett}
= {röd, gul, blå, violett} = {violett}Venndiagram
Vi använder nu Venndiagram för att illustrera sambanden mellan mängder. I slutet av 1800-talet utvecklade en engelsk logiker vid namn John Venn en metod för att representera förhållandet mellan mängder. Han representerade dessa relationer med hjälp av diagram, som nu är kända som Venn-diagram. Ett Venn-diagram representerar en mängd som det inre av en cirkel. Ofta är två eller flera cirklar inneslutna i en rektangel där rektangeln representerar den universella mängden. Det är enkelt att visualisera en skärning eller union av en mängd. I det här avsnittet kommer vi främst att använda Venn-diagram för att sortera olika populationer och räkna föremål.
|
(a) |
(b) |
(c) |
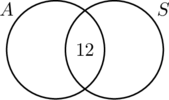
För att 30 personer körde bilar med automatisk växellåda, måste cirkeln A innehålla 30 element. Det betyder att x + 12 = 30, eller x = 18. På samma sätt, eftersom 20 personer körde bilar med standardväxellåda måste cirkeln B innehålla 20 element, eller y +12 = 20 vilket i sin tur gör att y = 8.
Nu när all information är sorterad är det lätt att utläsa av diagrammet att 18 personer körde bilar med enbart automatiska växellådor, 12 personer körde båda typerna av bilar och 8 personer körde bilar med enbart standardväxellådor. Därför deltog 18 + 12 + 8 = 38 personer i undersökningen.
|
(a) |
(b) |
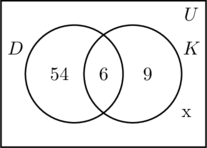
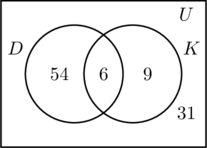
Vi fyller de tre regionerna som är kopplade till mängderna D och K på samma sätt som tidigare. Eftersom 100 personer deltog i undersökningen måste rektangeln som representerar den universella mängden U innehålla 100 objekt. Låt x representera de personer i den universella mängden som varken ingår i mängden D eller K. Detta innebär att 54 + 6 + 9 + x = 100, eller x = 31.
Därmed finns det 31 personer i undersökningen som inte har besökt någon av de båda platserna.
- 50 joggar, 30 simmar och 35 cyklar
- 14 joggar och simmar
- 7 simmar och cyklar
- 9 joggar och cyklar
- 3 personer deltar i alla tre aktiviteter
Lösning
|
(a) |
(b) |
(c) |
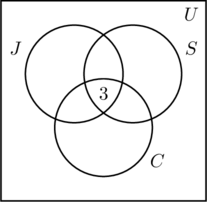
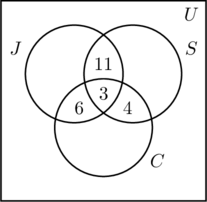
Vi placerar en 3 i den innersta regionen i figur (a) eftersom den representerar antalet personer som deltar i alla tre aktiviteter. Därefter beräknar vi x, y och z.
- Eftersom 14 personer joggar och simmar blir x +3 = 14, eller x = 11.
- Det faktum att 9 personer joggar och cyklar resulterar i y + 3 = 9, eller y = 6.
- Då 7 personer simmar och cyklar blir z + 3 = 7, eller z = 4.
- Denna information visas i figur (b).
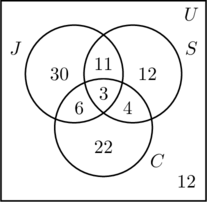
- Då 50 personer joggar, blir m + 11 + 6 + 3 = 50, eller m = 30.
- 30 personer simmar, därför är n + 11 + 4 + 3 = 30, eller n = 12.
- 35 personer cyklar, därför är p + 6 + 4 + 3 = 35, eller p = 22.
- Om vi adderar alla poster i alla tre uppsättningarna får vi summan 88. Eftersom 100 personer har undersökts är antalet inom den universella uppsättningen men utanför alla tre uppsättningarna 100 – 88 eller 12.
- I figur (c) är informationen sorterad och frågorna kan lätt besvaras.
Praktikfrågor
1. Låt den universella mängden U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h} och W = {a, c, e, g, i}. Ange medlemmarna i följande uppsättningar:
a. 
b. 
2. Överväg följande mängder: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, influensa, Norovirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella} och C = {SARS, Listeria, Tuberkulos, H5N1, Salmonella, HIV, COVID-19}. Ange medlemmarna i följande uppsättningar:
a. 
b. 
3. En undersökning bland idrottare visade att för sina mindre värk och smärtor använde 30 aspirin, 50 ibuprofen och 15 både och. Alla tillfrågade idrottare använde minst ett av de två smärtstillande läkemedlen. Hur många idrottare tillfrågades?
4. En undersökning av 150 gymnasieelever visade att 25 rapporterade att de tidigare haft en hjärnskakning eller huvudskada, 52 rapporterade att de upplevt psykisk ohälsa och 15 rapporterade båda resultaten. Hur många elever rapporterade inte något av resultaten?
5. En undersökning av 100 studenter vid Ryerson University visar att 50 prenumererar på Netflix, 40 prenumererar på Amazon Prime och 30 prenumererar på Disney+. Av dessa prenumererar 15 på både Netflix och Amazon Prime, 10 på både Amazon Prime och Disney+, 10 på både Netflix och Disney+ och 5 har alla tre prenumerationstjänsterna. Rita ett Venn-diagram och bestäm följande:
a. Antalet elever som prenumererar på Amazon Prime men inte på de två andra streamingtjänsterna.
b. Antalet studenter som prenumererar på Netflix eller Amazon Prime men inte på Disney+.
c. Antalet studenter som inte prenumererar på någon av dessa tjänster.