Inter-rater agreement Kappas

i.a.k.a. inter-rater reliability eller concordance

I statistik är inter-rater reliability, inter-rater agreement eller concordance graden av överensstämmelse mellan bedömare. Den ger en poäng på hur mycket homogenitet, eller konsensus, det finns i de betyg som bedömarna ger.

De Kappas som behandlas här är mest lämpliga för ”nominella” data. Den naturliga ordningen i uppgifterna (om någon sådan finns) ignoreras av dessa metoder. Om du ska använda dessa metoder ska du se till att du är medveten om begränsningarna.

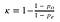
Det finns två delar till detta:

1. Beräkna observerad överensstämmelse
2. Beräkna slumpmässig överensstämmelse

Låt oss säga att vi har att göra med ”ja”- och ”nej”-svar och två bedömare. Här är bedömningarna:

rater1 = 
rater2 = 

Omvandla dessa bedömningar till en förvirringsmatris:

Observed agreement = (6 + 1) / 10 = 0.7
Chance agreement = probability of randomly saying yes (P_yes) + probability of randomly saying no (P_no)
P_yes = (6 + 1) / 10 * (6 + 1) / 10 = 0.49
P_no = (1 + 1) / 10 * (1 + 1) / 10 = 0.04
Chance agreement = 0.49 + 0.04 = 0.53

Då den observerade överensstämmelsen är större än slumpmässigt uppnådda överensstämmelser får vi en positiv Kappa.

kappa = 1 - (1 - 0.7) / (1 - 0.53) = 0.36

Och använd bara sklearns implementering

from sklearn.metrics import cohen_kappa_scorecohen_kappa_score(rater1, rater2)

som ger 0,35714.

Tolkning av Kappa

Specialfall

Mindre än slumpmässigt överensstämmande

rater1 = 
rater2 = 
cohen_kappa_score(rater1, rater2)
-0.2121

Om alla betyg är lika och motsatta

Detta fall ger tillförlitligt ett kappa på 0

rater1 = * 10
rater2 = * 10
cohen_kappa_score(rater1, rater2)
0.0

Random betyg

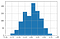
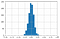
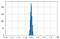
För slumpmässiga betyg följer Kappa en normalfördelning med ett medelvärde omkring noll.

När antalet betyg ökar finns det mindre variabilitet i värdet av Kappa i fördelningen.

Du kan hitta mer information här

Bemärk att Cohen’s Kappa endast gällde för två bedömare som bedömde exakt samma objekt.