En grupp 
är en ändlig eller oändlig mängd element tillsammans med en binär operation (kallad gruppoperation) som tillsammans uppfyller de fyra grundläggande egenskaperna slutenhet, associativitet, identitetsegenskap och inversegenskap. Den operation med avseende på vilken en grupp definieras kallas ofta ”gruppoperation”, och en mängd sägs vara en grupp ”under” denna operation. Elementen 
, 
, 
, … med binär operation mellan 
och 
betecknad 
bildar en grupp om
1. Stängning: Om 
och 
är två element i 
, så är produkten 
också i 
.
2. Associativitet: Den definierade multiplikationen är associativ, dvs. för alla 
, 
.
3. Identitet: Det finns ett identitetselement 
(även kallat 1, 
eller 
) så att 
för varje element 
.
4. Invers: Det måste finnas en invers (även kallad reciprok) till varje element. Därför innehåller mängden för varje element 
av 
ett element 
så att 
.
En grupp är en monoid vars alla element är inverterbara.
En grupp måste innehålla minst ett element, med den unika (upp till isomorfism) enelementgruppen som kallas trivialgruppen.
Studien av grupper kallas gruppteori. Om det finns ett ändligt antal element kallas gruppen för en ändlig grupp och antalet element kallas för gruppens gruppordning. En delmängd av en grupp som är sluten under gruppoperationen och den omvända operationen kallas en undergrupp. Undergrupper är också grupper, och många vanligt förekommande grupper är i själva verket speciella undergrupper till någon mer allmän större grupp.
Ett grundläggande exempel på en ändlig grupp är den symmetriska gruppen 
, som är gruppen av permutationer (eller ”under permutation”) av 
objekt. Den enklaste oändliga gruppen är mängden av heltal under vanlig addition. För kontinuerliga grupper kan man betrakta de reella talen eller mängden 
inverterbara matriser. De två sistnämnda är exempel på Lie-grupper.
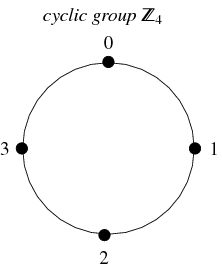
En mycket vanlig typ av grupp är de cykliska grupperna. Denna grupp är isomorf till gruppen av heltal (modulo 
), betecknas 
, 
eller 
och är definierad för varje heltal 
. Den är sluten under addition, associativ och har unika inverser. Talen från 0 till 
representerar dess element, där identitetselementet representeras av 0, och inversen av 
representeras av 
.
En karta mellan två grupper som bevarar identiteten och gruppoperationen kallas en homomorfism. Om en homomorfism har en invers som också är en homomorfism kallas den en isomorfism och de två grupperna kallas isomorfa. Två grupper som är isomorfa till varandra anses vara ”samma” när de betraktas som abstrakta grupper. Till exempel är gruppen av rotationer av en kvadrat, som illustreras nedan, den cykliska gruppen 
.
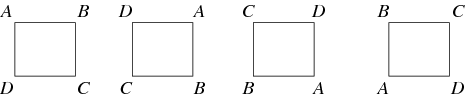
I allmänhet är en gruppaktion när en grupp agerar på en mängd, genom att permutera dess element, så att kartan från gruppen till permutationsgruppen för mängden är en homomorfism. Till exempel är rotationerna av en kvadrat en undergrupp till permutationerna av dess hörn. En viktig grupphandling för varje grupp 
är dess handling på sig själv genom konjugering. Detta är bara några av de möjliga gruppautomorfismerna. En annan viktig typ av gruppverkan är en grupprepresentation, där gruppen verkar på ett vektorrum genom inverterbara linjära kartor. När vektorrummets fält är de komplexa talen kallas ibland en representation för en CG-modul.
Grupphandlingar, och i synnerhet representationer, är mycket viktiga i tillämpningar, inte bara inom gruppteorin, utan även inom fysik och kemi. Eftersom en grupp kan betraktas som ett abstrakt matematiskt objekt kan samma grupp förekomma i olika sammanhang. Det är därför användbart att tänka på en representation av gruppen som en särskild inkarnation av gruppen, som också kan ha andra representationer. En irreducible representation av en grupp är en representation för vilken det inte finns någon enhetlig transformation som omvandlar representationsmatrisen till blockdiagonal form. De irreducerbara representationerna har ett antal anmärkningsvärda egenskaper, som formaliserats i grupportogonalitetssatsen.