Articles

Fysik

admin0

Lärandemål

I slutet av det här avsnittet kommer du att kunna:

  • Beskriv ett typiskt experiment med fotoelektrisk effekt.
  • Bestämma den maximala kinetiska energin hos fotoelektroner som kastas ut av fotoner med en viss energi eller våglängd, när man får den maximala kinetiska energin hos fotoelektroner för en annan fotonenergi eller våglängd.

När ljus träffar material kan det kasta ut elektroner från dem. Detta kallas den fotoelektriska effekten, vilket innebär att ljus (foto) producerar elektricitet. En vanlig användning av den fotoelektriska effekten är i ljusmätare, t.ex. de som justerar den automatiska irisen på olika typer av kameror. På ett liknande sätt är en annan användning solceller, som du förmodligen har i din miniräknare eller har sett på ett hustak eller en skylt vid vägkanten. Dessa utnyttjar den fotoelektriska effekten för att omvandla ljus till elektricitet för att driva olika apparater.

Figur 1. Den fotoelektriska effekten kan observeras genom att låta ljus falla på metallplattan i detta evakuerade rör. Elektroner som kastas ut av ljuset samlas in på kollektortråden och mäts som en ström. En fördröjningsspänning mellan kollektortråden och plattan kan sedan justeras för att bestämma energin hos de utskjutna elektronerna. Om spänningen till exempel är tillräckligt negativ kommer inga elektroner att nå ledningen. (kredit: P.P. Urone)

Denna effekt har varit känd i mer än ett sekel och kan studeras med hjälp av en anordning som den som visas i figur 1. Denna figur visar ett evakuerat rör med en metallplatta och en kollektortråd som är anslutna till en variabel spänningskälla, med kollektorn mer negativ än plattan. När ljus (eller annan EM-strålning) träffar plattan i det evakuerade röret kan den kasta ut elektroner. Om elektronerna har en energi i elektronvolt (eV) som är större än potentialdifferensen mellan plattan och ledningen i volt, kommer en del elektroner att samlas på ledningen. Eftersom elektronenergin i eV är eV, där q är elektronladdningen och V är potentialskillnaden, kan elektronenergin mätas genom att justera fördröjningsspänningen mellan tråden och plattan. Den spänning som hindrar elektronerna från att nå tråden är lika med energin i eV. Om t.ex. -3,00 V knappt stoppar elektronerna är deras energi 3,00 eV. Antalet elektroner som kastas ut kan bestämmas genom att mäta strömmen mellan tråden och plattan. Ju mer ljus, desto fler elektroner; en liten krets gör att den här apparaten kan användas som en ljusmätare.

Vad som verkligen är viktigt med den fotoelektriska effekten är vad Albert Einstein härledde ur den. Einstein insåg att det fanns flera egenskaper hos den fotoelektriska effekten som endast kunde förklaras om EM-strålning i sig är kvantiserad: den till synes kontinuerliga strömmen av energi i en EM-våg består i själva verket av energikvanter som kallas fotoner. I sin förklaring av den fotoelektriska effekten definierade Einstein en kvantiserad enhet eller kvantum av EM-energi, som vi nu kallar en foton, med en energi som är proportionell mot EM-strålningens frekvens. I ekvationsform är fotonenergin E = hf, där E är energin hos en foton med frekvensen f och h är Plancks konstant. Denna revolutionerande idé ser ut att likna Plancks kvantisering av energitillstånd i svartkroppsoscillatorer, men den är helt annorlunda. Det är kvantiseringen av själva EM-strålningen. EM-vågor består av fotoner och är inte kontinuerliga jämna vågor som beskrivs i tidigare kapitel om optik. Deras energi absorberas och avges i klumpar, inte kontinuerligt. Detta stämmer exakt överens med Plancks kvantisering av energinivåer i svartkroppsoscillatorer, eftersom dessa oscillatorer ökar och minskar sin energi i steg om hf genom att absorbera och avge fotoner som har E = hf. Vi observerar inte detta med våra ögon, eftersom det finns så många fotoner i vanliga ljuskällor att enskilda fotoner går obemärkt förbi. (Se figur 2.) Nästa avsnitt i texten (Fotonenergier och det elektromagnetiska spektrumet) ägnas åt en diskussion om fotoner och några av deras egenskaper och konsekvenser. Tills vidare kommer vi att använda fotonbegreppet för att förklara den fotoelektriska effekten, ungefär som Einstein gjorde.

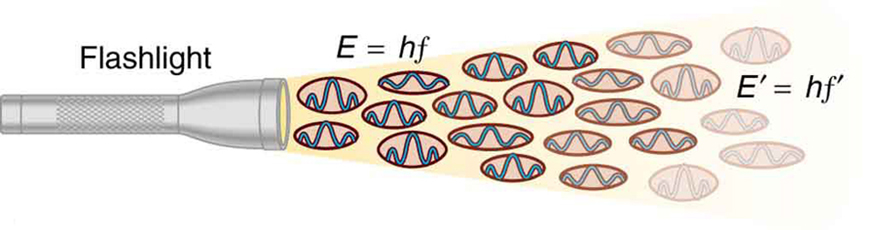
Figur 2. En EM-våg med frekvensen f består av fotoner, eller enskilda kvanta av EM-strålning. Energin för varje foton är E = hf, där h är Plancks konstant och f är frekvensen för EM-strålningen. Högre intensitet innebär fler fotoner per ytenhet. Ficklampan avger ett stort antal fotoner med många olika frekvenser, därför har andra fotoner energi E′ = hf′, och så vidare.

Den fotoelektriska effekten har de egenskaper som diskuteras nedan. Alla dessa egenskaper stämmer överens med tanken att enskilda fotoner av EM-strålning absorberas av enskilda elektroner i ett material, varvid elektronen får fotons energi. Några av dessa egenskaper är oförenliga med idén att EM-strålning är en enkel våg. Låt oss för enkelhetens skull betrakta vad som händer med monokromatisk EM-strålning där alla fotoner har samma energi hf.

  1. Om vi varierar frekvensen av den EM-strålning som faller på ett material finner vi följande: För ett givet material finns det en tröskelfrekvens f0 för EM-strålningen under vilken inga elektroner skjuts ut, oavsett intensitet. Enskilda fotoner interagerar med enskilda elektroner. Om fotonenergin är för liten för att bryta loss en elektron, kommer inga elektroner att skjutas ut. Om EM-strålning var en enkel våg skulle tillräcklig energi kunna erhållas genom att öka intensiteten.
  2. När EM-strålning faller på ett material kastas elektroner ut utan fördröjning. Så snart en enskild foton med tillräckligt hög frekvens absorberas av en enskild elektron kastas elektronen ut. Om EM-strålningen vore en enkel våg skulle det krävas flera minuter för att tillräcklig energi ska deponeras på metallytan för att kasta ut en elektron.
  3. Antalet elektroner som kastas ut per tidsenhet är proportionellt mot EM-strålningens intensitet och inte mot någon annan egenskap. EM-strålning med hög intensitet består av ett stort antal fotoner per ytenhet, där alla fotoner har samma karakteristiska energi hf.
  4. Om vi varierar EM-strålningens intensitet och mäter energin hos de utkastade elektronerna finner vi följande: Den maximala kinetiska energin hos utkastade elektroner är oberoende av EM-strålningens intensitet. Eftersom det finns så många elektroner i ett material är det ytterst osannolikt att två fotoner kommer att interagera med samma elektron samtidigt och därigenom öka den givna energin. Istället (som noterats i 3 ovan) resulterar ökad intensitet i att fler elektroner med samma energi skjuts ut. Om EM-strålning var en enkel våg skulle en högre intensitet kunna ge mer energi, och elektroner med högre energi skulle skjutas ut.
  5. Den kinetiska energin hos en utskjuten elektron är lika med fotonenergin minus elektronens bindningsenergi i det specifika materialet. En enskild foton kan ge all sin energi till en elektron. Fotonens energi används delvis för att bryta loss elektronen från materialet. Resten går till den utskjutna elektronens rörelseenergi. I ekvationsform ges detta genom KEe = hf – BE, där KEe är den utskjutna elektronens maximala rörelseenergi, hf är fotonens energi och BE är elektronens bindningsenergi till det specifika materialet. (BE kallas ibland för materialets arbetsfunktion.) Denna ekvation, som Einstein fick 1905, förklarar den fotoelektriska effektens egenskaper på ett kvantitativt sätt. En enskild foton av EM-strålning (den kommer inte på något annat sätt) interagerar med en enskild elektron och tillför tillräckligt med energi, BE, för att bryta loss den, medan resten går till rörelseenergi. Bindningsenergin är BE = hf0, där f0 är tröskelfrekvensen för det aktuella materialet. Figur 3 visar ett diagram över maximal KEe i förhållande till frekvensen av den infallande EM-strålning som faller på ett visst material.

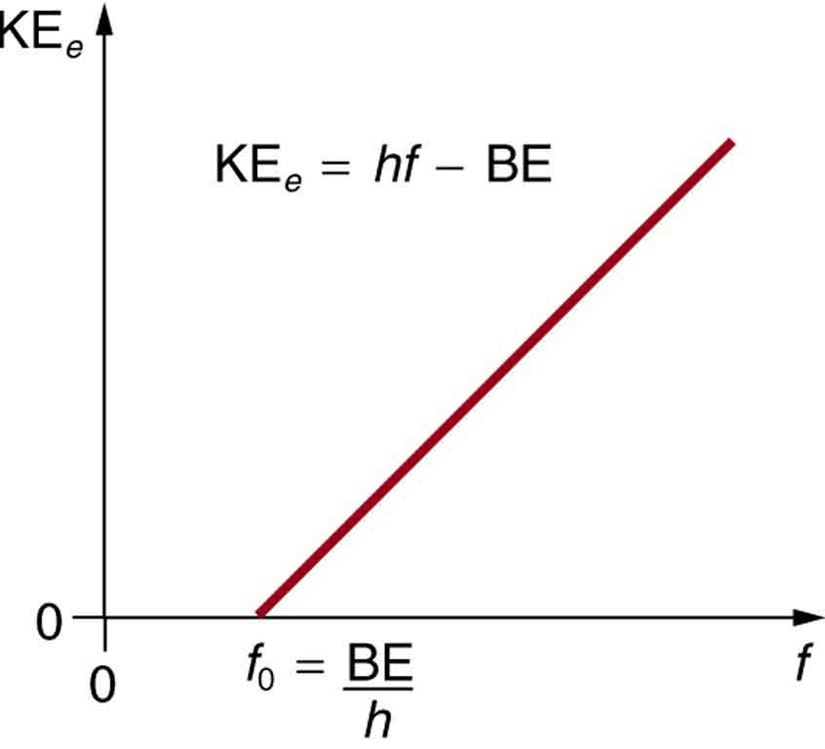
Figur 3. Fotoelektrisk effekt. Diagram över den kinetiska energin hos en utskjuten elektron, KEe, mot frekvensen av den EM-strålning som faller på ett visst material. Det finns en tröskelfrekvens under vilken inga elektroner kastas ut, eftersom den enskilda fotonen som interagerar med en enskild elektron inte har tillräcklig energi för att bryta loss den. Över tröskelenergin ökar KEe linjärt med f, vilket överensstämmer med KEe = hf – BE. Lutningen på denna linje är h – uppgifterna kan användas för att experimentellt bestämma Plancks konstant. Einstein gav den första framgångsrika förklaringen till sådana data genom att föreslå idén om fotoner – kvanta av EM-strålning.

Einsteins idé om att EM-strålning är kvantiserad var avgörande för kvantmekanikens början. Det är ett mycket mer allmänt begrepp än vad dess förklaring av den fotoelektriska effekten skulle kunna antyda. All EM-strålning kan också modelleras i form av fotoner, och EM-strålningens egenskaper är helt förenliga med detta faktum. (Som vi kommer att se i nästa avsnitt kan många aspekter av EM-strålning, t.ex. farorna med ultraviolett (UV) strålning, endast förklaras med hjälp av fotonernas egenskaper). Einstein, som är mer känd för den moderna relativitetsteorin, planterade ett viktigt frö för kvantmekaniken 1905, samma år som han publicerade sin första artikel om den speciella relativitetsteorin. Hans förklaring av den fotoelektriska effekten låg till grund för Nobelpriset som tilldelades honom 1921. Även om hans andra bidrag till den teoretiska fysiken också uppmärksammades i det priset, erkändes inte den speciella och allmänna relativitetsteorin fullt ut trots att de delvis hade verifierats genom experiment 1921. Trots att han dyrkades som hjälte fick denna stora man aldrig något Nobelpris för sitt mest berömda arbete – relativitetsteorin.

Exempel 1. Beräkning av fotonenergi och den fotoelektriska effekten: Ett violett ljus

1. Vad är energin i joule och elektronvolt för en foton av 420 nm violett ljus?

2. Vad är den maximala kinetiska energin för de elektroner som kastas ut från kalcium av 420 nm violett ljus, med tanke på att elektronernas bindningsenergi (eller arbetsfunktion) för kalciummetallen är 2,71 eV?

Strategi

För att lösa del 1, observera att energin för en foton ges av E = hf. För del 2 är det, när fotonens energi väl är beräknad, en enkel tillämpning av KEe = hf – BE för att hitta den utskjutna elektronens maximala rörelseenergi, eftersom BE är given.

Lösning för del 1

Fotonens energi ges av E = hf.

Då vi får våglängden snarare än frekvensen, löser vi det välkända förhållandet c = fλ för frekvensen, vilket ger f=\frac{c}{\lambda}\\\.

Kombinera dessa två ekvationer och få fram det användbara förhållandet E=\frac{hc}{\lambda}\\\.

Nu får man genom att ersätta kända värden

\displaystyle{E}=\frac{\left(6.63\times10^{-34}\text{ J}\cdot\text{ s}\right)\left(3.00\times10^{8}\text{ m/s}\right)}{420\times10^{-9}\text{ m}}=4.74\times10^{-19}\text{ J}\\\

Omräknat till eV är fotonens energi

\displaystyle{E}=\left(4.47\times10^{-19}\text{ J}\right)\frac{1\text{ eV}}}{1.6\times10^{-19}\text{ J}}}=2.96\text{ eV}\\\

Lösning för del 2

Finnandet av den kinetiska energin hos den utskjutna elektronen är nu en enkel tillämpning av ekvationen KEe = hf – BE. Genom att ersätta fotonenergin och bindningsenergin får man KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV.

Diskussion

Energin i denna 420-nm-foton av violett ljus är en liten bråkdel av en joule, och det är därför inte så konstigt att en enskild foton skulle vara svår att uppfatta direkt för oss – människor är mer inställda på energier i storleksordningen joule. Men om vi tittar på energin i elektronvolt kan vi se att denna foton har tillräckligt med energi för att påverka atomer och molekyler. En DNA-molekyl kan till exempel brytas med cirka 1 eV energi, och typiska atomära och molekylära energier är i storleksordningen eV, så UV-fotonen i det här exemplet skulle kunna ha biologiska effekter. Den utskjutna elektronen (som kallas fotoelektron) har en ganska låg energi och skulle inte färdas långt, utom i ett vakuum. Elektronen skulle stoppas av en fördröjningspotential på endast 0,26 eV. Om fotonens våglängd var längre och dess energi mindre än 2,71 eV skulle formeln ge en negativ kinetisk energi, vilket är omöjligt. Detta innebär helt enkelt att 420-nm-fotonerna med sin energi på 2,96 eV inte ligger mycket över frekvenströskeln. Du kan själv visa att tröskelvåglängden är 459 nm (blått ljus). Detta innebär att om kalciummetall används i en ljusmätare kommer mätaren att vara okänslig för längre våglängder än det blå ljusets. En sådan ljusmätare skulle till exempel vara helt okänslig för rött ljus.

PhET Explorations: Se hur ljus slår ut elektroner från ett metallmål och återskapa experimentet som gav upphov till kvantmekaniken.

Klicka för att ladda ner simuleringen. Körs med Java.

Avsnittssammanfattning

  • Den fotoelektriska effekten är den process där EM-strålning kastar ut elektroner från ett material.
  • Einstein föreslog att fotoner ska vara kvanta av EM-strålning som har energin E = hf, där f är strålningens frekvens.
  • Alla EM-strålning består av fotoner. Som Einstein förklarade beror alla egenskaper hos den fotoelektriska effekten på växelverkan mellan enskilda fotoner och enskilda elektroner.
  • Den maximala rörelseenergin KEe hos utskjutna elektroner (fotoelektroner) ges av KEe = hf – BE, där hf är fotonenergin och BE är elektronens bindningsenergi (eller arbetsfunktion) till det aktuella materialet.

Begreppsfrågor

  1. Är synligt ljus den enda typen av EM-strålning som kan orsaka den fotoelektriska effekten?
  2. Vilka aspekter av den fotoelektriska effekten kan inte förklaras utan fotoner? Vilka kan förklaras utan fotoner? Är de senare inkonsekventa med existensen av fotoner?
  3. Är den fotoelektriska effekten en direkt följd av EM-strålningens vågkaraktär eller EM-strålningens partikelkaraktär? Förklara kortfattat.
  4. Insulatorer (icke-metaller) har en högre BE än metaller, och det är svårare för fotoner att kasta ut elektroner från isolatorer. Diskutera hur detta hänger samman med de fria laddningarna i metaller som gör dem till goda ledare.
  5. Om du tar upp och skakar en metallbit som har elektroner i sig som är fria att röra sig som en ström faller inga elektroner ut. Men om man värmer metallen kan elektroner kokas bort. Förklara båda dessa fakta i förhållande till mängden och fördelningen av den energi som är involverad i att skaka föremålet jämfört med att värma det.

Problem &Övningar

  1. Vilken EM-strålning med den längsta våglängden som kan kasta ut en fotoelektron från silver, med tanke på att bindningsenergin är 4,73 eV? Ligger detta inom det synliga området?
  2. Hitta den foton med längst våglängd som kan kasta ut en elektron från kalium, med tanke på att bindningsenergin är 2,24 eV. Är detta synlig EM-strålning?
  3. Vad är bindningsenergin i eV för elektroner i magnesium, om den längsta våglängdsfotonen som kan kasta ut elektroner är 337 nm?
  4. Beräkna bindningsenergin i eV för elektroner i aluminium, om den längsta våglängdsfotonen som kan kasta ut dem är 304 nm.
  5. Vad är den maximala kinetiska energin i eV hos de elektroner som kastas ut från natriummetall av EM-strålning på 450 nm, givet att bindningsenergin är 2,28 eV?
  6. UV-strålning med en våglängd på 120 nm faller på guldmetall, till vilken elektroner är bundna med 4,82 eV. Vad är den maximala kinetiska energin hos de utkastade fotoelektronerna?
  7. Violett ljus med våglängden 400 nm kastar ut elektroner med en maximal kinetisk energi på 0,860 eV från natriummetall. Vad är elektronernas bindningsenergi till natriummetall?
  8. UV-strålning med en våglängd på 300 nm faller på uranmetall och kastar ut elektroner med 0,500 eV. Vad är elektronernas bindningsenergi till uranmetall?
  9. (a) Vad är våglängden för EM-strålning som kastar ut 2,00 eV elektroner från kalciummetall, givet att bindningsenergin är 2,71 eV? (b) Vilken typ av EM-strålning är detta?
  10. Hitta våglängden för fotoner som kastar ut 0,100 eV elektroner från kalium, givet att bindningsenergin är 2,24 eV. Är dessa fotoner synliga?
  11. Vad är den maximala hastigheten för de elektroner som kastas ut från ett material av 80-nm-fotoner, om de är bundna till materialet med 4,73 eV?
  12. Fotoelektroner från ett material med en bindningsenergi på 2,71 eV kastas ut av 420-nm-fotoner. När de har kastats ut, hur lång tid tar det för dessa elektroner att färdas 2,50 cm till en detektionsanordning?
  13. En laser med en uteffekt på 2,00 mW vid en våglängd på 400 nm projiceras på kalciummetall. (a) Hur många elektroner per sekund skjuts ut? (b) Vilken effekt förs bort av elektronerna, med tanke på att bindningsenergin är 2,71 eV?
  14. (a) Beräkna antalet fotoelektroner per sekund som kastas ut från ett område på 1,00 mm 2 av natriummetall genom EM-strålning på 500 nm med en intensitet på 1,30 kW/m2 (intensiteten hos solljuset ovanför jordens atmosfär). (b) Med tanke på att bindningsenergin är 2,28 eV, vilken effekt förs bort av elektronerna? (c) Elektronerna bär med sig mindre energi än vad som förs in av fotonerna. Vart tar den andra energin vägen? Hur kan den återvinnas?
  15. Oförnuftiga resultat. Rött ljus med en våglängd på 700 nm projiceras på magnesiummetall till vilken elektroner är bundna med 3,68 eV. (a) Använd KEe = hf – BE för att beräkna den kinetiska energin hos de utskjutna elektronerna. (b) Vad är orimligt med detta resultat? (c) Vilka antaganden är orimliga eller inkonsekventa?
  16. Orimliga resultat. (a) Vad är elektronernas bindningsenergi till ett material från vilket elektroner på 4,00 eV kastas ut av EM-strålning på 400 nm? (b) Vad är orimligt med detta resultat? (c) Vilka antaganden är orimliga eller inkonsekventa?

Glossar

fotoelektrisk effekt: Fenomenet där vissa material kastar ut elektroner när ljus lyser på dem

foton: Ett kvantum, eller en partikel, av elektromagnetisk strålning

foton energi: E = hf

Bindningsenergi: även kallad arbetsfunktion; den energimängd som krävs för att kasta ut en elektron från ett material

Utvalda lösningar på problem & Övningar

1. 263 nm

3. 3,69 eV

5. 0,483 eV

7. 2,25 eV

9. (a) 264 nm; (b) ultraviolett

11. 1,95 × 106 m/s

13. (a) 4,02 × 1015 s; (b) 0,256 mW

15. (a) -1,90 eV; (b) negativ rörelseenergi; (c) att elektronerna skulle slås fria

.

Lämna ett svar

Din e-postadress kommer inte publiceras.