Vattens fasdiagram
Figur 11.23 ”Två versioner av vattnets fasdiagram” visar vattnets fasdiagram och illustrerar att vattnets trippelpunkt inträffar vid 0,01 °C och 0,00604 atm (4,59 mmHg). Trippelpunkten (273,16 K) är mycket mer reproducerbar än isens smältpunkt, som beror på mängden löst luft och det atmosfäriska trycket, och används för att definiera den absoluta temperaturskalan (Kelvin). Trippelpunkten representerar också det lägsta tryck vid vilket en flytande fas kan existera i jämvikt med fast substans eller ånga. Vid tryck under 0,00604 atm smälter is därför inte till vätska när temperaturen ökar, utan det fasta materialet sublimerar direkt till vattenånga. Sublimation av vatten vid låg temperatur och lågt tryck kan användas för att ”frystorka” livsmedel och drycker. Livsmedlet eller drycken kyls först ned till minusgrader och placeras i en behållare där trycket hålls under 0,00604 atm. När temperaturen sedan höjs sublimerar vattnet och lämnar kvar den uttorkade maten (som den som används av backpackers eller astronauter) eller den pulveriserade drycken (som med frystorkat kaffe).
Fasdiagrammet för vatten som illustreras i del (b) i figur 11.23 ”Två versioner av vattens fasdiagram” visar gränsen mellan is och vatten i en utvidgad skala. Smältkurvan för is lutar uppåt och något åt vänster snarare än uppåt och åt höger som i figur 11.22 ”Ett typiskt fasdiagram för en substans som uppvisar tre faser – fast, flytande och gas – och en superkritisk region”; det vill säga isens smältpunkt sjunker med ökande tryck; vid 100 MPa (987 atm) smälter isen vid -9 °C. Vatten beter sig på detta sätt eftersom det är ett av de få kända ämnen för vilka det kristallina fasta ämnet är mindre tätt än vätskan (andra är bland annat antimon och vismut). Om trycket på is som är i jämvikt med vatten vid 0 °C och 1 atm ökas tenderar vissa av molekylerna att tryckas närmare varandra, vilket minskar provets volym. Volymminskningen (och motsvarande ökning av densiteten) är mindre för ett fast ämne eller en vätska än för en gas, men den är tillräcklig för att smälta en del av isen.
Figur 11.23 Två versioner av vattnets fasdiagram
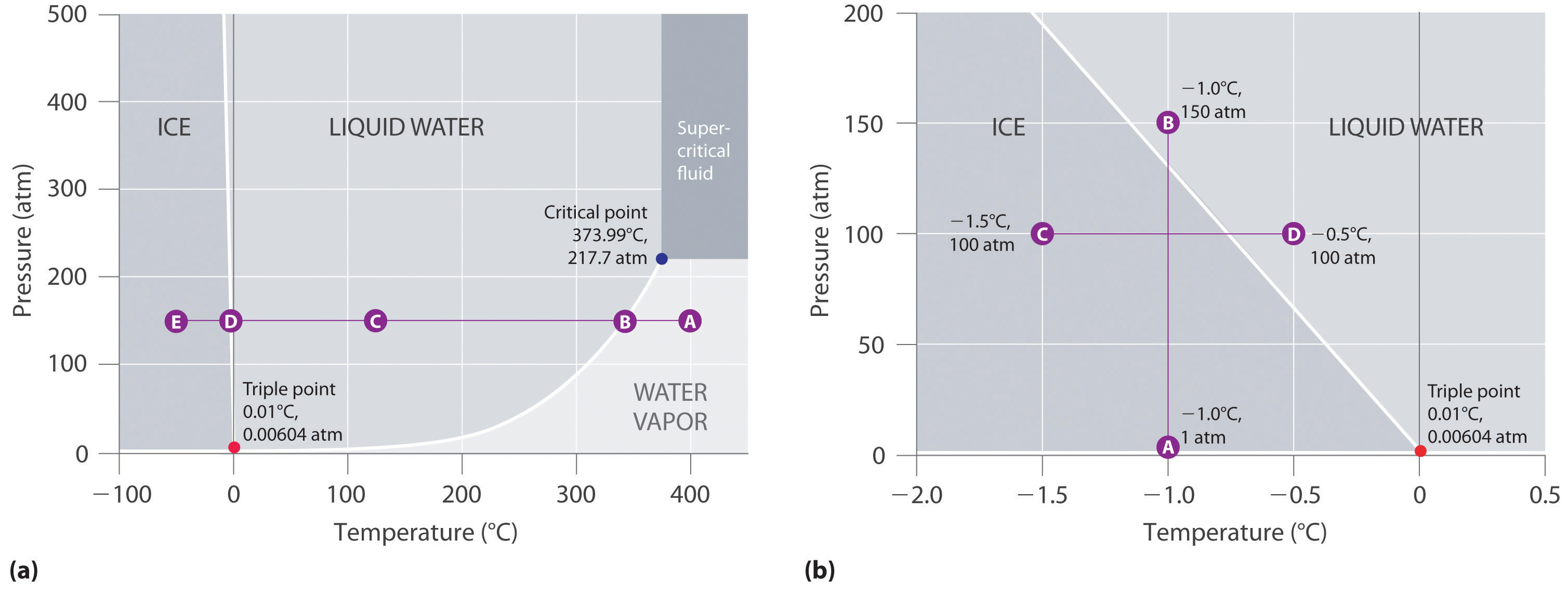
(a) I den här grafen med linjära temperatur- och tryckaxlar är gränsen mellan is och flytande vatten nästan vertikal. (b) Denna graf med en expanderad skala illustrerar minskningen av smältpunkten med ökande tryck. (Bokstäverna hänvisar till punkter som diskuteras i exempel 10.)
I del (b) i figur 11.23 ”Två versioner av vattnets fasdiagram” är punkt A belägen vid P = 1 atm och T = -1,0 °C, inom fasdiagrammets fasta (is) region. När trycket ökar till 150 atm samtidigt som temperaturen förblir densamma, korsar linjen från punkt A gränsen mellan is och vatten till punkt B, som ligger i området för flytande vatten. Om man tillämpar ett tryck på 150 atm kommer is att smälta vid -1,0 °C. Vi har redan påpekat att tryckberoendet för vattnets smältpunkt är av avgörande betydelse. Om gränsen mellan fast och flytande ämne i vattnets fasdiagram skulle luta uppåt och åt höger i stället för åt vänster skulle isen vara tätare än vatten, iskuber skulle sjunka, vattenledningar skulle inte spricka när de fryser och frostskyddsmedel skulle vara onödiga i bilmotorer.
Intill helt nyligen beskrev många läroböcker skridskoåkning som möjlig eftersom trycket som alstras av skridskoåkaren med sin skridskoklinga är tillräckligt högt för att smälta isen under skridskoklingan och på så sätt skapa ett smörjande skikt av flytande vatten som gör det möjligt för skridskoåkaren att glida över isen. Även om denna förklaring är intuitivt tillfredsställande är den felaktig, vilket vi kan visa genom en enkel beräkning. Minns du från kapitel 10 ”Gaser” att trycket (P) är den kraft (F) som utövas per ytenhet (A):
Ekvation 11.4
P = F A
För att beräkna det tryck som en skridskoåkare utövar på isen behöver vi bara beräkna den utövade kraften och skridskoklingans area. Om vi antar en skridskoåkare på 75,0 kg (165 lb) är den kraft som skridskoåkaren utövar på isen på grund av gravitationen
Ekvation 11.5
F = mg
där m är massan och g är den acceleration som beror på jordens gravitation (9,81 m/s2). Kraften är alltså
Ekvation 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Om vi antar att skridskoklingorna är 2.0 mm breda och 25 cm långa, så är arean på botten av varje blad
Ekvation 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Om skridskoåkaren glider på en fot är trycket på isen
Svenska 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
Trycket är mycket lägre än det tryck som krävs för att sänka isens smältpunkt med ens 1 °C, och erfarenheten visar att det är möjligt att åka skridskor även när temperaturen ligger långt under fryspunkten. Tryckinducerad smältning av isen kan således inte förklara den låga friktion som gör att skridskoåkare (och hockeypuckar) kan glida. Ny forskning tyder på att isens yta, där den ordnade ordningen av vattenmolekyler möter luften, består av ett eller flera lager av nästan flytande vatten. Dessa lager, tillsammans med den smältning som orsakas av friktionen när en skridskoåkare skjuter framåt, tycks förklara både hur lätt en skridskoåkare glider och det faktum att det blir svårare att åka skridskor vid temperaturer under cirka -7 °C, när antalet smörjande vattenlager på ytan minskar.
