Datastrukturer 101: Arrays – en visuell introduktion för nybörjare

Lär känna de datastrukturer som du använder varje dag.

👋 Välkommen! Låt oss börja med lite viktig kontext. Låt mig fråga dig följande:
✅ Lyssnar du på musik på din smartphone?
✅ Har du en kontaktlista på din telefon?
✅ Har du någonsin sett en leaderboard under en tävling?

Om du svarar ”ja” på någon av de här frågorna är det nästan säkert att du har använt arrays utan att du ens visste det! 😃 Arrays är mycket kraftfulla datastrukturer som lagrar listor med element. De har oändliga användningsområden. De är mycket viktiga i datavetenskapens värld.

I den här artikeln kommer du att lära dig för- och nackdelar med arrays, deras struktur, operationer och användningsområden.

Vi börjar! 👍

🔎 Djupdykning i arrays grundläggande struktur

För att förstå hur de fungerar är det till stor hjälp att visualisera datorns minne som ett rutnät, precis som i bilden nedan. Varje information lagras i ett av de små element (rutor) som utgör rutnätet.

Arrays drar nytta av denna ”rutnätsstruktur” för att lagra listor med relaterad information på intilliggande minnesplatser för att garantera extrem effektivitet när det gäller att hitta dessa värden. 🔳🔳🔳🔳 🔳

Du kan tänka på matriser så här:

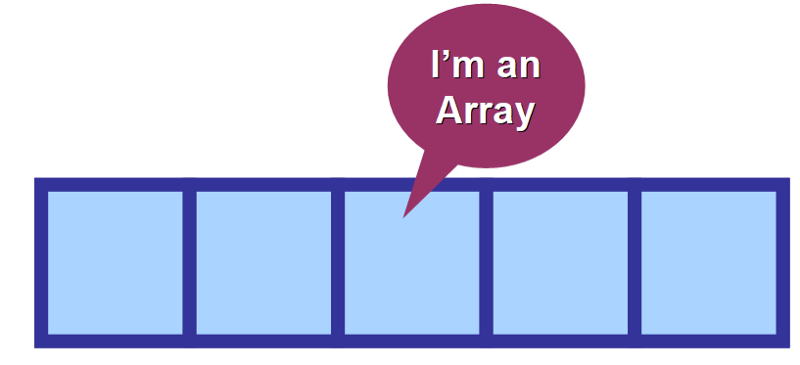
Dess element ligger bredvid varandra i minnet. Om du behöver komma åt mer än ett av dem är processen extremt optimerad eftersom datorn redan vet var värdet finns.

Grymt, eller hur? Låt oss lära oss hur detta fungerar bakom kulisserna! 😃

📚 Klassificering

Arrayer klassificeras som homogena datastrukturer eftersom de lagrar element av samma typ.

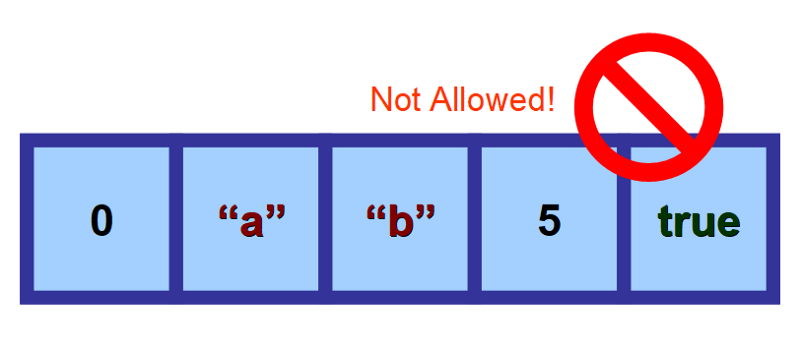
De kan lagra siffror, strängar, boolska värden (sant och falskt), tecken, objekt och så vidare. Men när du väl har definierat vilken typ av värden som din array ska lagra måste alla dess element vara av samma typ. Du kan inte ”blanda” olika typer av data.

👀 Läsa värden – magin börjar!

Den fantastiska kraften hos matriser kommer från deras effektivitet när det gäller att komma åt värden. Detta uppnås tack vare dess rutnätliknande struktur. Låt oss ta en titt på detta mer i detalj.🔍

När du skapar en array gör du:
– Tilldela den till en variabel. 👈
– Definiera vilken typ av element den ska lagra. 🎈
– Definiera dess storlek (det maximala antalet element). 📚

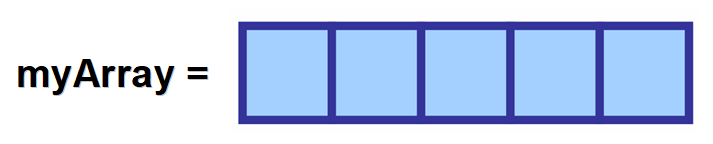
💡 Observera: Det namn som du tilldelar den här variabeln är mycket viktigt eftersom du kommer att använda det senare i din kod för att få tillgång till värden och för att ändra matrisen.

Men hur kan du tala om för datorn vilket specifikt värde du vill komma åt? Här spelar index en viktig roll!

1️⃣ Index

Du använder vad som kallas ett ”index” (”index” i plural) för att komma åt ett värde i en array. Detta är ett nummer som hänvisar till den plats där värdet är lagrat.

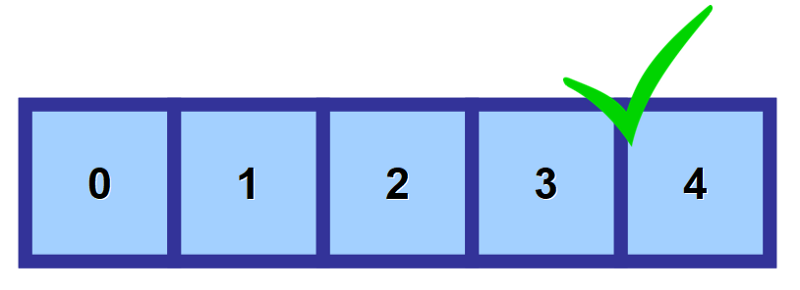
Som du kan se i diagrammet nedan hänvisas till det första elementet i matrisen med hjälp av index 0. När du rör dig längre åt höger ökar indexet med ett för varje plats i minnet.

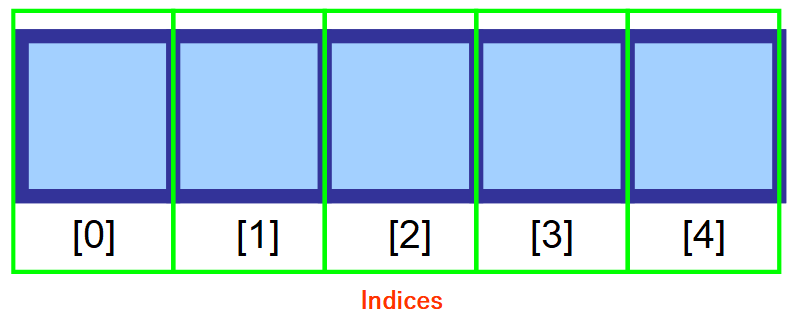
💡 Obs: Jag vet att det först verkar konstigt att börja räkna från 0 i stället för 1, men detta kallas för nollbaserad numrering. Det är mycket vanligt inom datavetenskap.

Den allmänna syntaxen för att komma åt ett element är: <ArrayVariable>

Till exempel:
Om din matris är lagrad i variabeln myArray och du vill komma åt det första elementet (vid index 0) använder du myArray

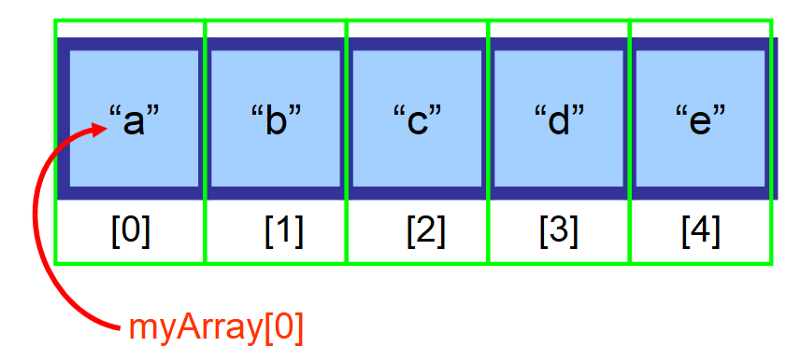
2️⃣ Minne

Nu när du vet hur du kan komma åt värden, ska vi se hur matriser lagras i datorns minne. När du definierar storleken på matrisen är allt det utrymmet i minnet ”reserverat” från och med det ögonblicket för framtida värden som du kanske vill infoga.

💡 Observera: Om du inte fyller matrisen med värden kommer det utrymmet att hållas reserverat och tomt tills du gör det.

Till exempel:
Vad sägs om att du definierar en matris med storleken 5 men bara infogar ett värde. Allt det återstående utrymmet kommer att vara tomt och ”reserverat” i minnet i väntan på framtida tilldelningar.

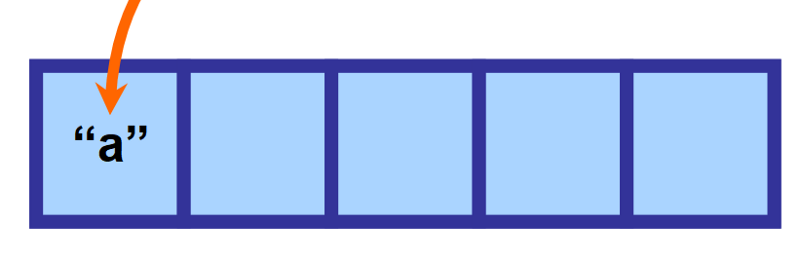
Detta är viktigt eftersom matriser är extremt effektiva när det gäller att komma åt värden eftersom alla element lagras i sammanhängande utrymmen i minnet. På så sätt vet datorn exakt var den ska leta för att hitta den information du begärde.

Men… det finns en nackdel 😞 eftersom detta inte är minneseffektivt. Du reserverar minne för framtida operationer som kanske inte inträffar. Det är därför arrayer rekommenderas i situationer där du i förväg vet hur många element du ska lagra.

🔧 Operationer – bakom kulisserna!

När du nu vet vad arrayer är när de används och hur de lagrar element, ska vi dyka ner i deras operationer som insättning och borttagning.

1️⃣ Insättning – välkommen!

Vad sägs om att vi har en array med storlek 6 och att det fortfarande finns ett tomt utrymme. Vi vill infoga ett element ”e” i början av matrisen (index 0), men denna plats är redan upptagen av elementet ”a”. Vad ska vi göra?

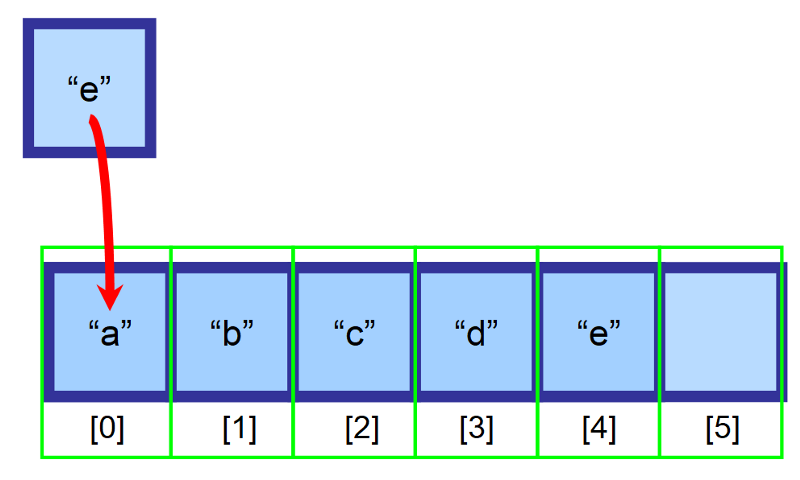
För att infoga i matriser flyttar vi alla element som ligger till höger om infogningsstället, ett index till höger. Element ”a” kommer nu att ligga på index 1, element ”b” kommer att ligga på index 2 och så vidare…

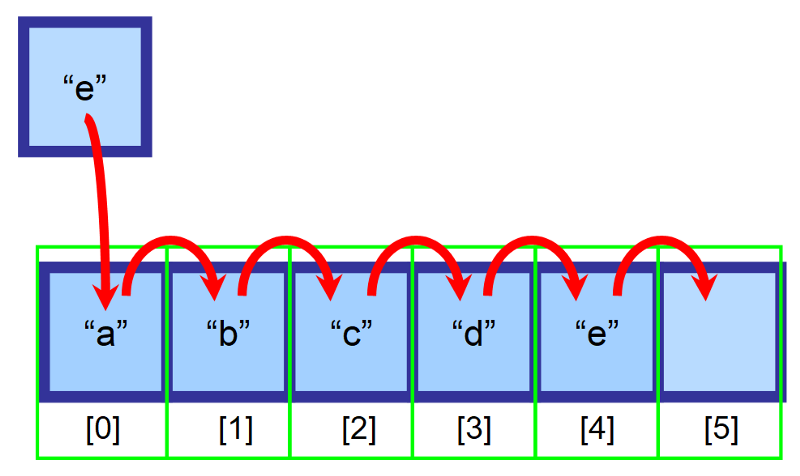
💡 Obs: Du kommer att behöva skapa en variabel för att hålla reda på det sista indexet som innehåller element. I diagrammet ovan är arrayen fylld upp till index 4 före insättningen. På så sätt kan du avgöra om arrayen är full och vilket index du ska använda för att infoga ett element i slutet.

Efter att ha gjort detta är vårt element framgångsrikt infogat. 👏

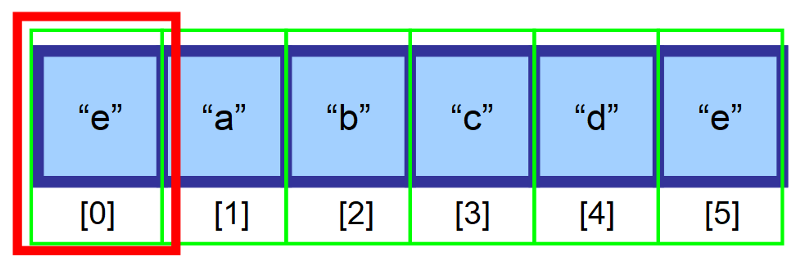
⚠️ Vänta lite! Vad händer om arrayen är full?

Vad tror du kommer att hända om arrayen är full och du försöker infoga ett element? 😱

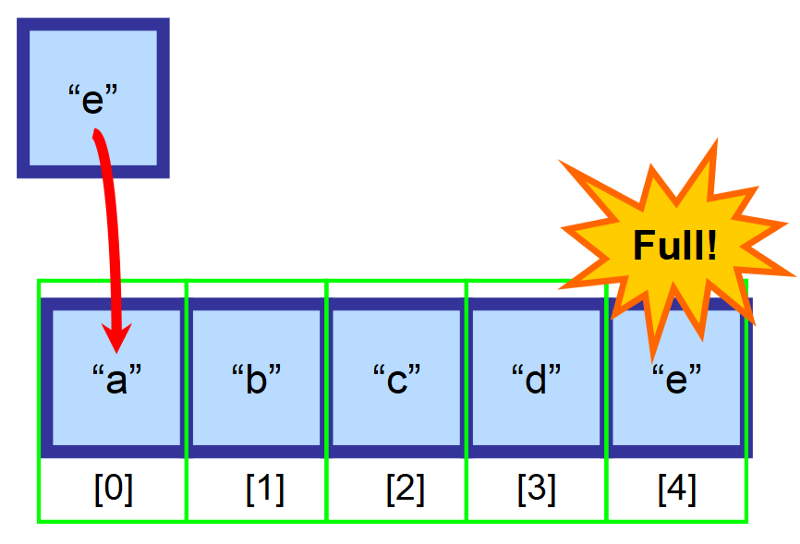
I det här fallet måste du skapa en ny, större array och manuellt kopiera alla element till denna nya array. Denna operation är mycket dyr, tidsmässigt. Föreställ dig vad som skulle hända om du hade en array med miljontals element! Det skulle kunna ta mycket lång tid att genomföra. ⏳

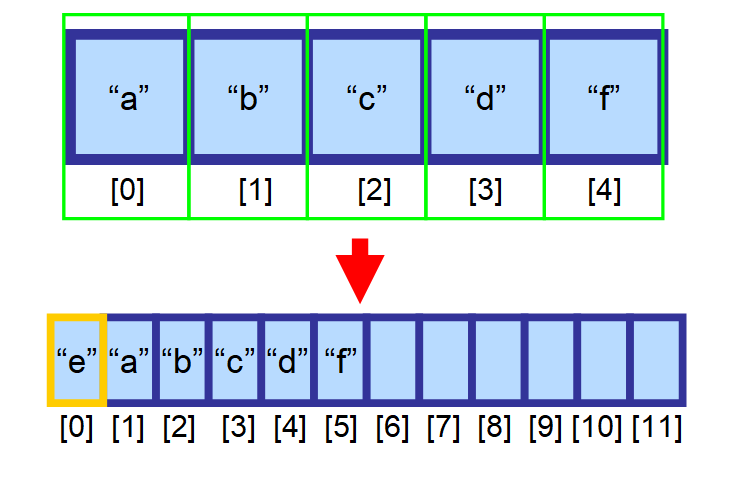
💡 Observera: Det enda undantaget från den här regeln, när infogningen är mycket snabb, är när du infogar ett element i slutet av matrisen (vid indexet som ligger till höger om det sista elementet) och det fortfarande finns plats. Detta görs på konstant tid O(1).

2️⃣ Radering- Bye, Bye!

Nu säger vi att du vill radera ett element från matrisen.

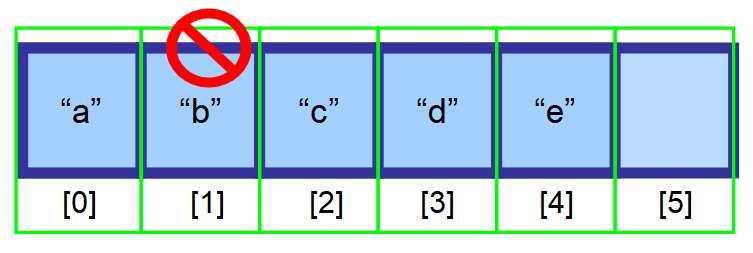
För att bibehålla effektiviteten för slumpmässig åtkomst (att kunna få tillgång till matrisen genom ett index extremt snabbt) måste elementen lagras i sammanhängande utrymmen av minnet. Du kan inte bara ta bort elementet och lämna det utrymmet tomt.

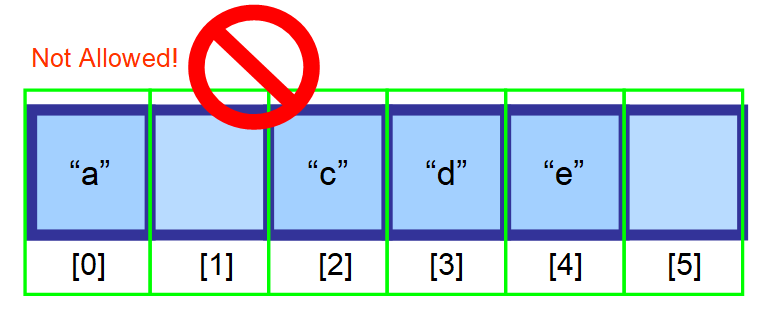
Du bör flytta de element som kommer efter det element som du vill ta bort ett index till vänster.

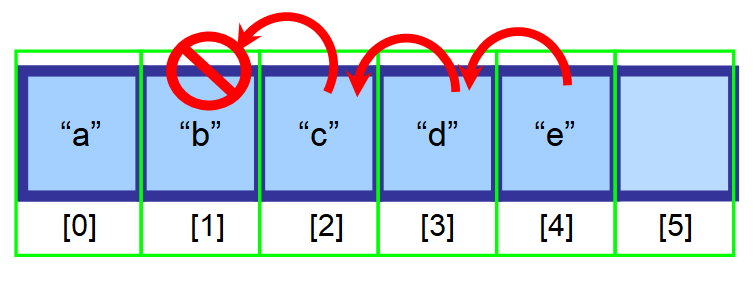
Och till slut har du den här resulterande matrisen 👇. Som du kan se har ”b” framgångsrikt tagits bort.

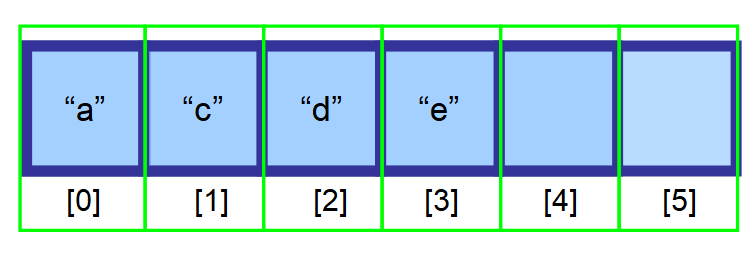
💡 Obs: Radering är mycket effektiv när du tar bort det sista elementet. Eftersom du måste skapa en variabel för att hålla reda på det sista indexet som innehåller element (i diagrammet ovan, index 3) kan du direkt ta bort det elementet med hjälp av indexet.

3️⃣ Hitta ett element

Du har tre alternativ för att hitta ett element i en array:

• Om du vet var det finns använder du indexet.
• Om du inte vet var det finns och dina data är sorterade kan du använda algoritmer för att optimera din sökning, till exempel binär sökning.
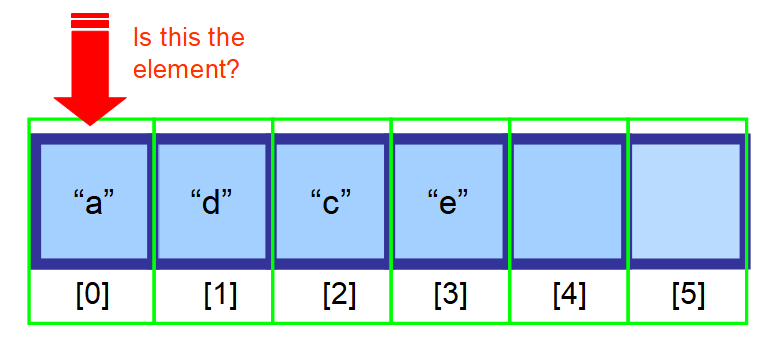
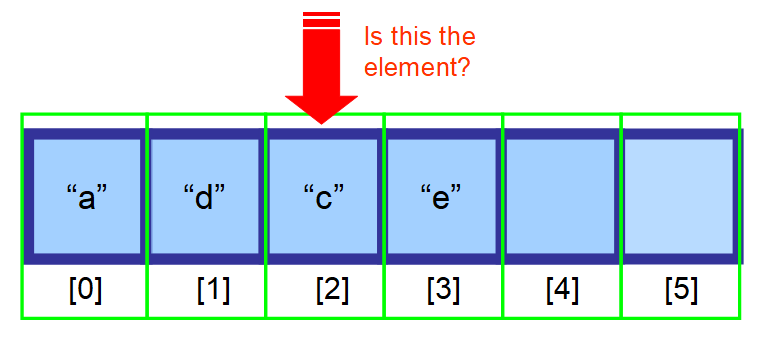
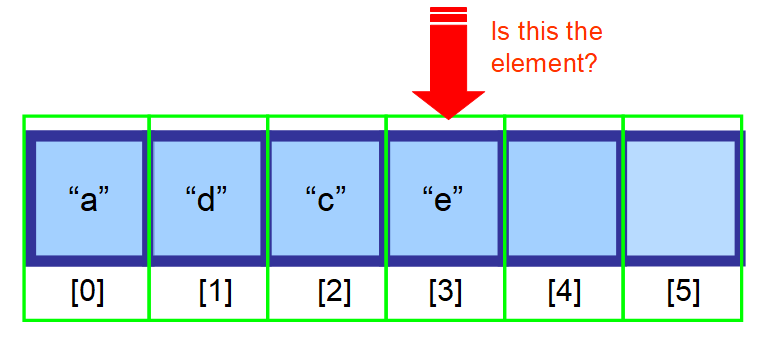
• Om du inte vet var det ligger och dina data inte är sorterade måste du söka igenom varje element i matrisen och kontrollera om det aktuella elementet är det element du letar efter (se sekvensen av diagram nedan).

👋 Sammanfattningsvis…

• Arrayer är extremt kraftfulla datastrukturer som lagrar element av samma typ. Elementens typ och arrayens storlek ligger fast och definieras när du skapar den.
• Minnet allokeras omedelbart efter att arrayen har skapats och är tomt tills du tilldelar värdena.
• Elementen ligger på sammanhängande platser i minnet, så de kan nås mycket effektivt (slumpmässig åtkomst, O(1) = konstant tid) med hjälp av index.
• Indexen börjar vid 0, inte vid 1 som vi är vana vid.
• Insättning av element i början eller i mitten av matrisen innebär att element flyttas till höger. Om matrisen är full, skapas en ny, större matris (vilket inte är särskilt effektivt). Att infoga i slutet av matrisen är mycket effektivt, konstant tid O(1).
• Att ta bort element från början eller mitten av matrisen innebär att alla element flyttas till vänster för att undvika att lämna ett tomt utrymme i minnet. Detta garanterar att elementen lagras i sammanhängande utrymmen i minnet. Att ta bort i slutet av matrisen är mycket effektivt eftersom du bara tar bort det sista elementet.
• För att hitta ett element måste du kontrollera hela matrisen tills du hittar det. Om uppgifterna är sorterade kan du använda algoritmer som binär sökning för att optimera processen.

”Lär dig av gårdagen, lev för idag, hoppas på morgondagen. Det viktiga är att inte sluta ifrågasätta.”
– Albert Einstein

👋 Tack!

Jag hoppas verkligen att du gillade min artikel. ❤️
Följ mig på Twitter för att hitta fler artiklar som denna. 😃