Funcții de bază
În această secțiune vom reprezenta grafic șapte funcții de bază care vor fi utilizate pe parcursul acestui curs. Fiecare funcție este reprezentată grafic prin trasarea unor puncte. Amintiți-vă că f(x)=y și astfel f(x) și y pot fi folosite interschimbabil.
Orice funcție de forma f(x)=c, unde c este un număr real oarecare, se numește funcție constantăOrice funcție de forma f(x)=c unde c este un număr real…. Funcțiile constante sunt liniare și se pot scrie f(x)=0x+c. În această formă, este clar că panta este 0 și intersecția y este (0,c). Evaluând orice valoare pentru x, cum ar fi x = 2, se va obține c.
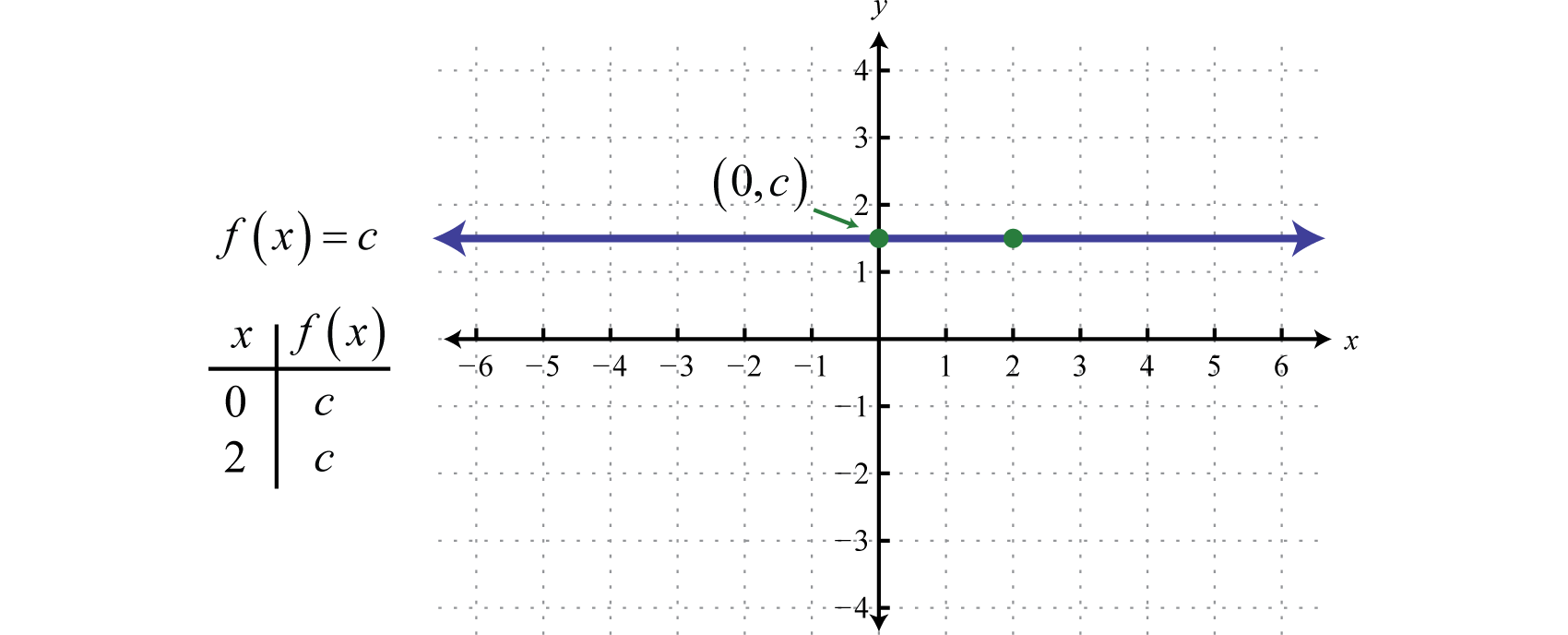
Graficul unei funcții constante este o linie orizontală. Domeniul este format din toate numerele reale ℝ și domeniul este format din singura valoare {c}.
În continuare definim funcția identitateFuncția liniară definită prin f(x)=x. f(x)=x. Evaluând orice valoare pentru x se va obține aceeași valoare. De exemplu, f(0)=0 și f(2)=2. Funcția identitate este liniară, f(x)=1x+0, cu panta m=1 și intersecția y (0, 0).
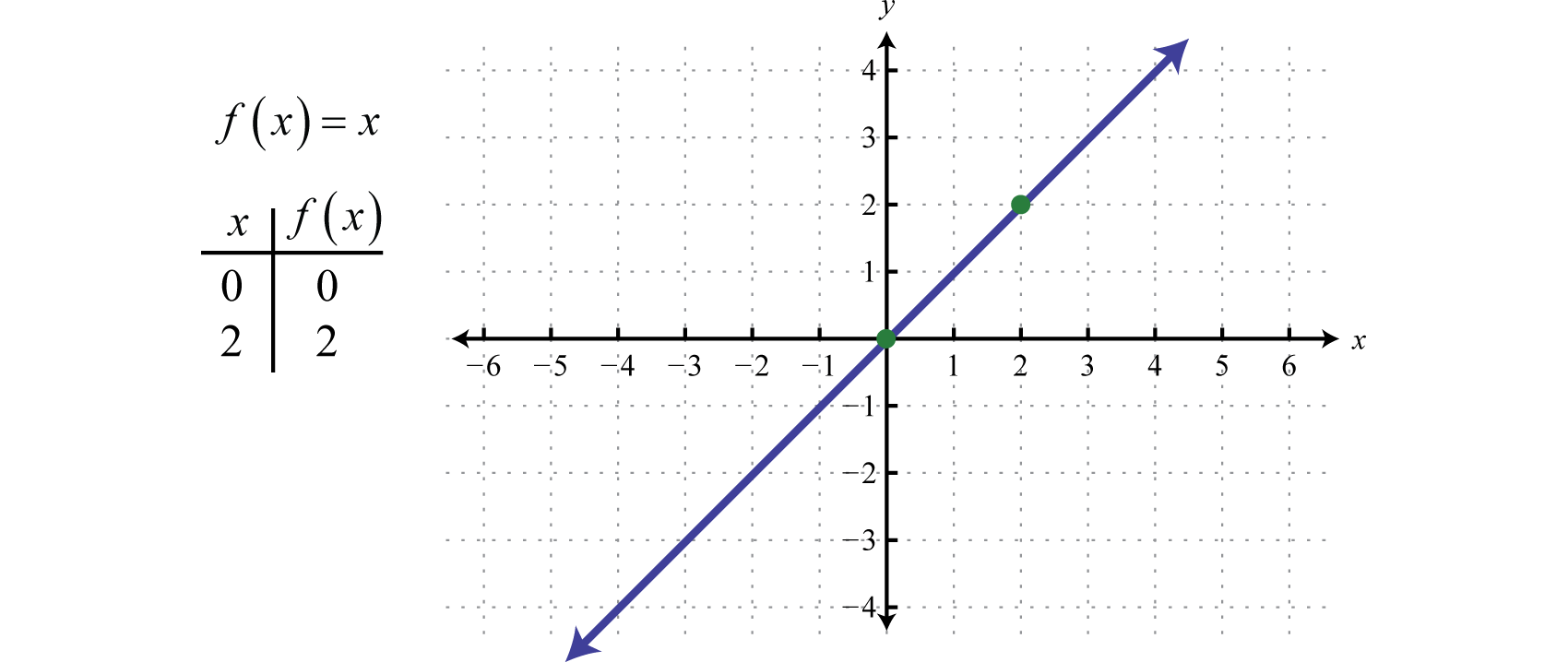
Domeniul și intervalul sunt ambele formate din toate numerele reale.
Funcția pătraticăFuncția pătratică definită de f(x)=x2., definită de f(x)=x2, este funcția obținută prin ridicarea la pătrat a valorilor din domeniu. De exemplu, f(2)=(2)2=4 și f(-2)=(-2)2=4. Rezultatul ridicării la pătrat a valorilor non-zero din domeniu va fi întotdeauna pozitiv.
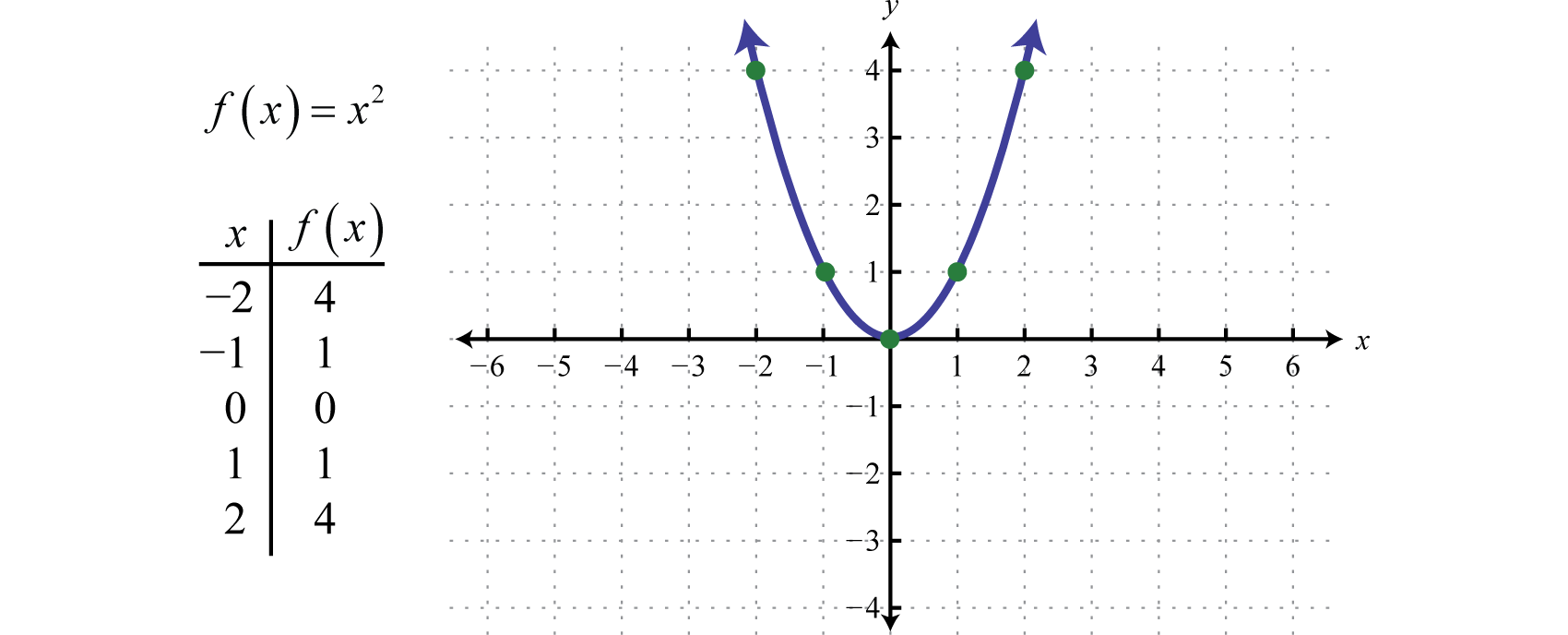
Graficul curbat rezultat se numește parabolăGraficul curbat format de funcția de ridicare la pătrat… Domeniul este format din toate numerele reale ℝ și intervalul este format din toate valorile y mai mari sau egale cu zero [0,∞).
Funcția de cubareFuncția de cubare definită de f(x)=x3., definită de f(x)=x3, ridică toate valorile din domeniu la puterea a treia. Rezultatele pot fi fie pozitive, fie zero, fie negative. De exemplu, f(1)=(1)3=1, f(0)=(0)3=0 și f(-1)=(-1)3=-1.
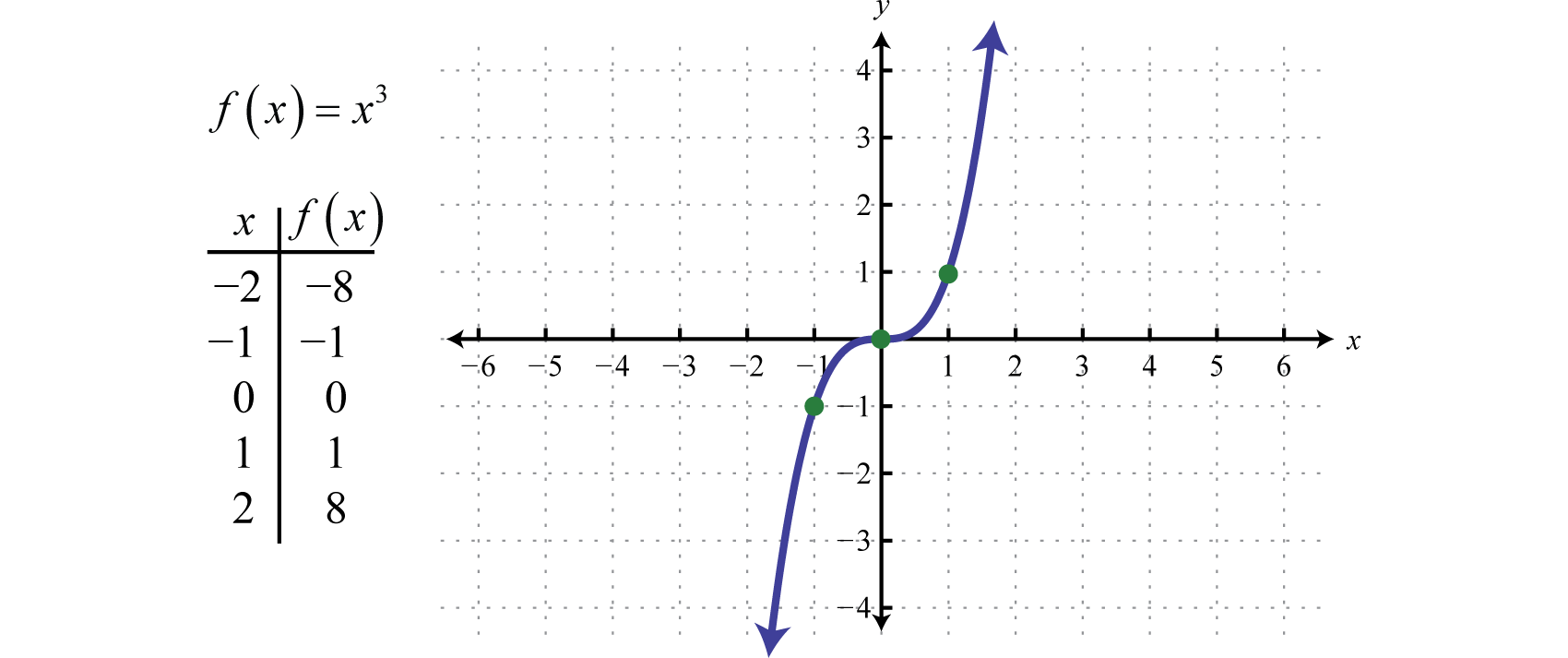
Domeniul și domeniul constau amândouă din toate numerele reale ℝ.
Rețineți că funcțiile constantă, identitate, pătrat și cubică sunt toate exemple de funcții polinomiale de bază. Următoarele trei funcții de bază nu sunt polinoame.
Funcția valoare absolutăFuncția definită de f(x)=|x|., definită de f(x)=|x|, este o funcție în care ieșirea reprezintă distanța față de origine pe o dreaptă numerică. Rezultatul evaluării funcției valorii absolute pentru orice valoare diferită de zero a lui x va fi întotdeauna pozitiv. De exemplu, f(-2)=|-2|=2 și f(2)=|2|=2.
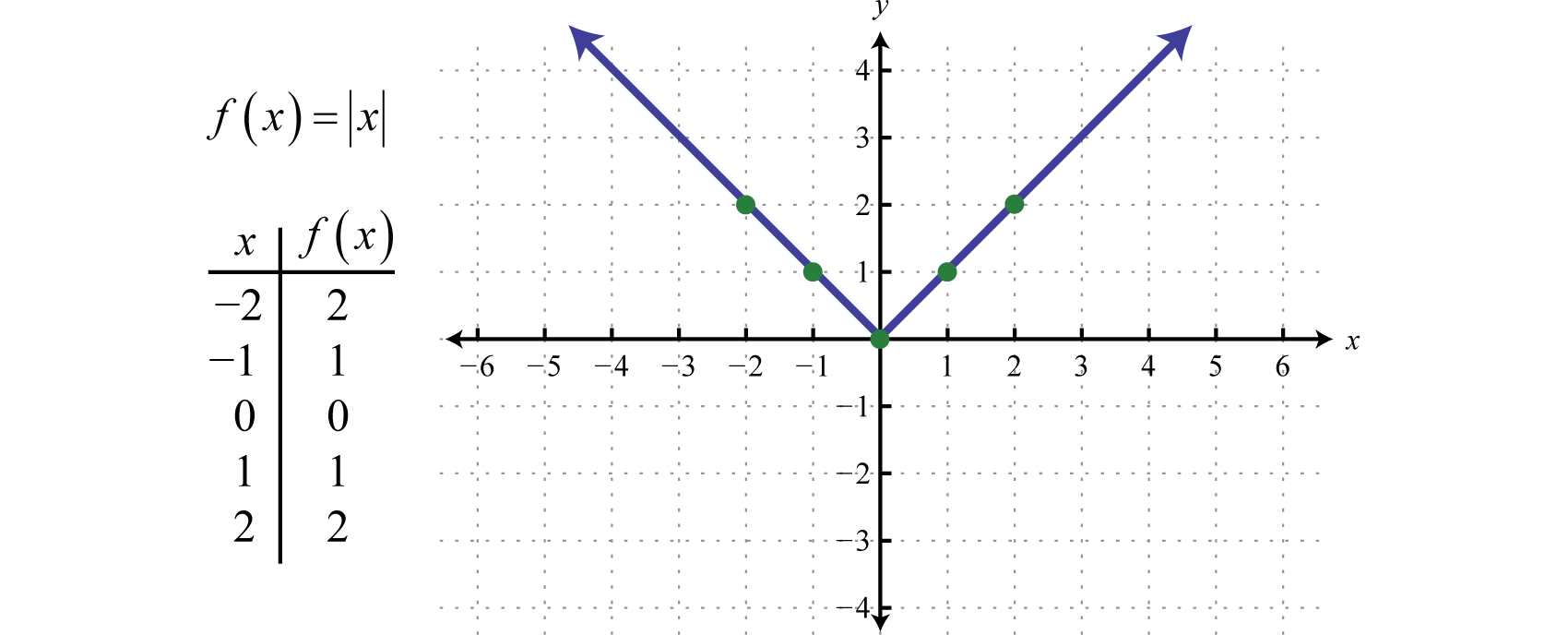
Domeniul funcției valoare absolută este format din toate numerele reale ℝ, iar domeniul este format din toate valorile lui y mai mari sau egale cu zero [0,∞).
Funcția rădăcină pătratăFuncția definită prin f(x)=x…, definită prin f(x)=x, nu este definită ca fiind un număr real dacă valorile lui x sunt negative. Prin urmare, cea mai mică valoare din domeniu este zero. De exemplu, f(0)=0=0 și f(4)=4=4=2.
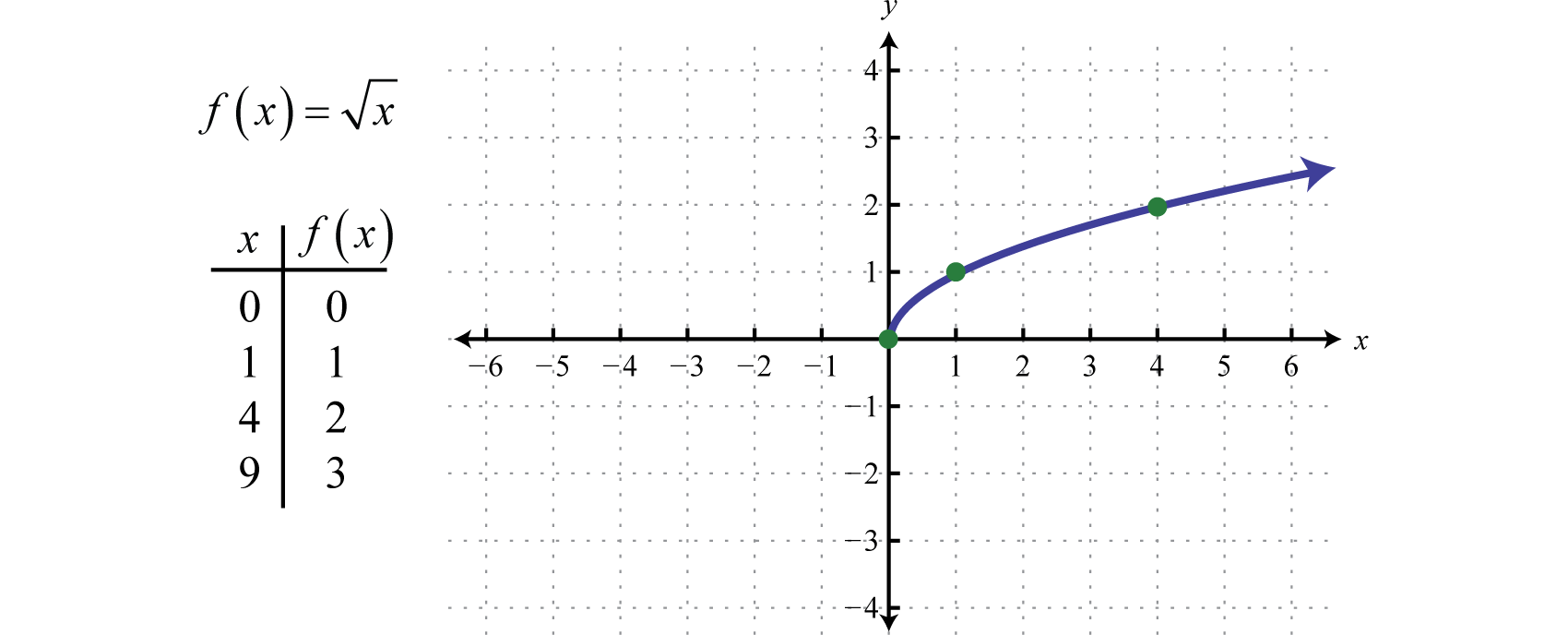
Domeniul și intervalul sunt ambele formate din numere reale mai mari sau egale cu zero [0,∞).
Funcția reciprocăFuncția definită de f(x)=1x., definită de f(x)=1x, este o funcție rațională cu o singură restricție pe domeniu, și anume x≠0. Reciproca unei valori a lui x foarte apropiate de zero este foarte mare. De exemplu,
f(1/10)=1(110)=1⋅101=10f(1/100)=1(1100)=1⋅1001=100f(1/1.000)=1(11.000)=1⋅1,0001=1.000
Cu alte cuvinte, pe măsură ce valorile x se apropie de zero, reciprocele lor vor tinde fie spre infinit pozitiv, fie spre infinit negativ. Acest lucru descrie o asimptotă verticalăO linie verticală de care un grafic se apropie la infinit. pe axa y. Mai mult, acolo unde valorile x sunt foarte mari, rezultatul funcției reciproce este foarte mic.
f(10)=110=0,1f(100)=1100=0,01f(1000)=11.000=0,001
Cu alte cuvinte, pe măsură ce valorile x devin foarte mari, valorile y rezultate tind spre zero. Acest lucru descrie o asimptotă orizontalăO linie orizontală de care un grafic se apropie la infinit atunci când valorile x tind spre ±∞. pe axa x. După trasarea unui număr de puncte se poate determina forma generală a funcției reciproce.
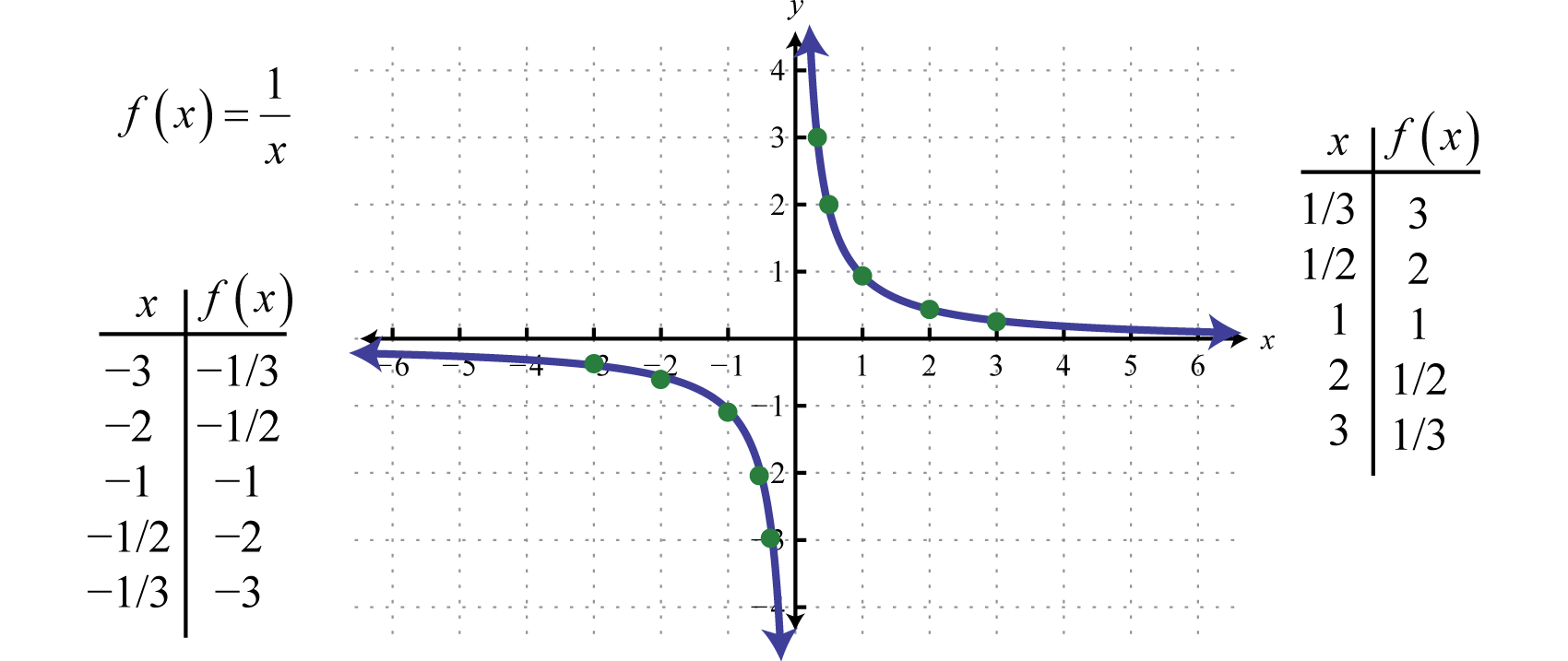
Atât domeniul, cât și intervalul funcției reciproce constau din toate numerele reale, cu excepția lui 0, care poate fi exprimat folosind notația de interval, după cum urmează: (-∞,0)∪(0,∞).
