Tycho BraheEditar

Tycho Brahe (1546-1601) fue un noble danés muy conocido como astrónomo en su época. Para seguir avanzando en la comprensión del cosmos se necesitaban nuevas observaciones más precisas que las que utilizaba Nicolás Copérnico, y Tycho hizo grandes progresos en este campo. Tycho formuló un geoheliocentrismo, es decir, que el Sol se movía alrededor de la Tierra mientras que los planetas orbitaban alrededor del Sol, conocido como el sistema de Tycho. Aunque Tycho apreciaba las ventajas del sistema de Copérnico, al igual que muchos otros no podía aceptar el movimiento de la Tierra.
En 1572, Tycho Brahe observó una nueva estrella en la constelación de Casiopea. Durante dieciocho meses, brilló en el cielo sin paralaje visible, lo que indicaba que formaba parte de la región celeste de las estrellas según el modelo de Aristóteles. Sin embargo, según ese modelo, no podía producirse ningún cambio en los cielos, por lo que la observación de Tycho supuso un gran descrédito para las teorías de Aristóteles. En 1577, Tycho observó un gran cometa en el cielo. Basándose en sus observaciones de paralaje, el cometa pasó por la región de los planetas. Según la teoría aristotélica, en esta región sólo existía el movimiento circular uniforme sobre esferas sólidas, por lo que era imposible que un cometa entrara en esta región. Tycho llegó a la conclusión de que no existían tales esferas, por lo que se planteó la cuestión de qué mantenía a un planeta en su órbita.
Con el patrocinio del rey de Dinamarca, Tycho Brahe estableció Uraniborg, un observatorio en Hven. Durante 20 años, Tycho y su equipo de astrónomos recopilaron observaciones astronómicas mucho más precisas que las realizadas anteriormente. Estas observaciones resultarían vitales en futuros avances astronómicos.
Johannes KeplerEditar

Kepler encontró empleo como ayudante de Tycho Brahe y, tras la inesperada muerte de éste, le sustituyó como matemático imperial del emperador Rodolfo II. Entonces pudo utilizar las extensas observaciones de Brahe para realizar notables avances en astronomía, como las tres leyes del movimiento planetario. Kepler no habría podido elaborar sus leyes sin las observaciones de Tycho, ya que éstas le permitieron demostrar que los planetas viajaban en elipses y que el Sol no se encuentra directamente en el centro de una órbita, sino en un foco. Galileo Galilei vino después de Kepler y desarrolló su propio telescopio con suficiente aumento para permitirle estudiar Venus y descubrir que tiene fases como una luna. El descubrimiento de las fases de Venus fue una de las razones más influyentes para la transición del geocentrismo al heliocentrismo. Los Philosophiæ Naturalis Principia Mathematica de Sir Isaac Newton concluyeron la revolución copernicana. El desarrollo de sus leyes del movimiento planetario y de la gravitación universal explicaba el presunto movimiento relacionado con los cielos al afirmar la existencia de una fuerza gravitatoria de atracción entre dos objetos.
En 1596, Kepler publicó su primer libro, el Mysterium Cosmographicum, que fue el segundo (después de Thomas Digges, en 1576) en avalar la cosmología copernicana por un astrónomo desde 1540. El libro describía su modelo que utilizaba las matemáticas pitagóricas y los cinco sólidos platónicos para explicar el número de planetas, sus proporciones y su orden. El libro se ganó el suficiente respeto de Tycho Brahe como para invitar a Kepler a Praga y servirle de ayudante.
En 1600, Kepler se puso a trabajar en la órbita de Marte, el segundo más excéntrico de los seis planetas conocidos en aquella época. Este trabajo fue la base de su siguiente libro, la Astronomia nova, que publicó en 1609. El libro defendía el heliocentrismo y las elipses para las órbitas planetarias en lugar de los círculos modificados por los epiciclos. Este libro contiene las dos primeras de sus epónimas tres leyes del movimiento planetario. En 1619, Kepler publicó su tercera y última ley que mostraba la relación entre dos planetas en lugar del movimiento de un solo planeta.
El trabajo de Kepler en astronomía fue nuevo en parte. A diferencia de los que le precedieron, descartó la suposición de que los planetas se movían con un movimiento circular uniforme, sustituyéndolo por un movimiento elíptico. Además, al igual que Copérnico, afirmó la realidad física de un modelo heliocéntrico frente a uno geocéntrico. Sin embargo, a pesar de todos sus avances, Kepler no pudo explicar la física que mantendría a un planeta en su órbita elíptica.
Leyes de Kepler del movimiento planetarioEditar
1. La ley de las elipses: Todos los planetas se mueven en órbitas elípticas, con el Sol en un foco. 2. La ley de las áreas iguales en tiempos iguales: Una línea que conecta un planeta con el Sol barre áreas iguales en tiempos iguales. 3. La Ley de la Armonía: El tiempo necesario para que un planeta orbite alrededor del Sol, llamado su período, es proporcional al eje largo de la elipse elevado a la potencia 3/2. La constante de proporcionalidad es la misma para todos los planetas.
Galileo GalileiEditar
Galileo Galilei fue un científico italiano al que a veces se denomina «padre de la astronomía observacional moderna». Sus mejoras en el telescopio, sus observaciones astronómicas y su apoyo al copernicanismo fueron parte integrante de la revolución copernicana.
Basándose en los diseños de Hans Lippershey, Galileo diseñó su propio telescopio que, al año siguiente, mejoró a 30 aumentos. Con este nuevo instrumento, Galileo realizó una serie de observaciones astronómicas que publicó en el Sidereus Nuncius en 1610. En este libro, describió la superficie de la Luna como áspera, desigual e imperfecta. También observó que «el límite que divide la parte brillante de la oscura no forma una línea uniformemente ovalada, como sucedería en un sólido perfectamente esférico, sino que está marcado por una línea desigual, rugosa y muy sinuosa, como muestra la figura». Estas observaciones desafiaron la afirmación de Aristóteles de que la Luna era una esfera perfecta y la idea más amplia de que los cielos eran perfectos e inmutables.
El siguiente descubrimiento astronómico de Galileo resultaría sorprendente. Mientras observaba a Júpiter en el transcurso de varios días, notó cuatro estrellas cercanas a Júpiter cuyas posiciones cambiaban de una manera que sería imposible si fueran estrellas fijas. Tras muchas observaciones, llegó a la conclusión de que esas cuatro estrellas orbitaban alrededor del planeta Júpiter y que, en realidad, eran lunas, no estrellas. Este descubrimiento fue radical porque, según la cosmología aristotélica, todos los cuerpos celestes giran alrededor de la Tierra y un planeta con lunas obviamente contradice esa creencia popular. Al mismo tiempo que contradecía la creencia aristotélica, apoyaba la cosmología copernicana, que afirmaba que la Tierra es un planeta como todos los demás.
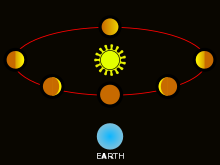
En 1610, Galileo observó que Venus tenía un conjunto completo de fases, similares a las fases de la Luna que podemos observar desde la Tierra. Esto era explicable por los sistemas copernicano o ticónico, que decían que todas las fases de Venus serían visibles debido a la naturaleza de su órbita alrededor del Sol, a diferencia del sistema ptolemaico, que afirmaba que sólo algunas de las fases de Venus serían visibles. Debido a las observaciones de Venus por parte de Galileo, el sistema de Ptolomeo pasó a ser muy sospechoso y la mayoría de los astrónomos más importantes se convirtieron posteriormente a varios modelos heliocéntricos, haciendo de su descubrimiento uno de los más influyentes en la transición del geocentrismo al heliocentrismo.
Esfera de las estrellas fijasEditar
En el siglo XVI, varios escritores inspirados por Copérnico, como Thomas Digges, Giordano Bruno y William Gilbert defendieron un universo indefinidamente extendido o incluso infinito, con otras estrellas como soles lejanos. Esto contrasta con la visión aristotélica de una esfera de estrellas fijas. Aunque Copérnico y Kepler se opusieron (sin que Galileo expresara su opinión), a mediados del siglo XVII esto se aceptó ampliamente, en parte debido al apoyo de René Descartes.
Isaac NewtonEditar

Newton fue un conocido físico y matemático inglés que fue conocido por su libro Philosophiæ Naturalis Principia Mathematica. Fue una figura principal de la Revolución Científica por sus leyes del movimiento y de la gravitación universal. Se dice que las leyes de Newton son el punto final de la Revolución Copernicana.
Newton utilizó las leyes del movimiento planetario de Kepler para derivar su ley de la gravitación universal. La ley de la gravitación universal de Newton fue la primera ley que desarrolló y propuso en su libro Principia. La ley establece que dos objetos cualesquiera ejercen una fuerza de atracción gravitatoria entre sí. La magnitud de la fuerza es proporcional al producto de las masas gravitatorias de los objetos, e inversamente proporcional al cuadrado de la distancia entre ellos. Junto con la ley de la gravitación universal de Newton, los Principia presentan también sus tres leyes del movimiento. Estas tres leyes explican la inercia, la aceleración, la acción y la reacción cuando se aplica una fuerza neta a un objeto.
Immanuel KantEditar
Immanuel Kant en su Crítica de la razón pura (edición de 1787) estableció un paralelismo entre la «revolución copernicana» y la epistemología de su nueva filosofía trascendental. La comparación de Kant se hace en el Prefacio a la segunda edición de la Crítica de la razón pura (publicada en 1787; una fuerte revisión de la primera edición de 1781). Kant sostiene que, al igual que Copérnico pasó de la suposición de que los cuerpos celestes giraban alrededor de un espectador inmóvil a un espectador en movimiento, la metafísica, «procediendo precisamente en la línea de la hipótesis primaria de Copérnico», debería pasar de suponer que «el conocimiento debe ajustarse a los objetos» a la suposición de que «los objetos deben ajustarse a nuestro conocimiento».
Se ha dicho mucho sobre lo que Kant quiso decir al referirse a su filosofía como «procediendo precisamente en las líneas de la hipótesis primaria de Copérnico». Ha habido una larga discusión sobre la idoneidad de la analogía de Kant porque, según la mayoría de los comentaristas, Kant invirtió el movimiento primario de Copérnico. Según Tom Rockmore, el propio Kant nunca utilizó la frase «revolución copernicana» sobre sí mismo, aunque fue aplicada «rutinariamente» a su obra por otros.
