Teste de Wald: Definição, Exemplos, Executando o Teste

Teste de Hipótese >Teste de Wald

O que é o Teste de Wald?

O teste de Wald pode dizer quais variáveis do modelo estão contribuindo com algo significativo.

O teste de Wald (também chamado teste de Wald Chi-Squared) é uma maneira de descobrir se as variáveis explicativas em um modelo são significativas. “Significantes” significa que elas adicionam algo ao modelo; variáveis que não adicionam nada podem ser excluídas sem afetar o modelo de qualquer forma significativa. O teste pode ser usado para uma multiplicidade de modelos diferentes, incluindo aqueles com variáveis binárias ou variáveis contínuas.
A hipótese nula para o teste é: algum parâmetro = algum valor. Por exemplo, você pode estar estudando se o peso é afetado por comer junk food duas vezes por semana. O “peso” seria o seu parâmetro. O valor poderia ser zero (indicando que você não acha que o peso é afetado por comer junk food). Se a hipótese nula for rejeitada, sugere que as variáveis em questão podem ser removidas sem grande prejuízo para o modelo encaixar.

• Se o teste de Wald mostrar que os parâmetros de certas variáveis explicativas são zero, você pode remover as variáveis do modelo.
• Se o teste mostrar que os parâmetros não são zero, você deve incluir as variáveis no modelo.

O teste de Wald é normalmente falado em termos de qui-quadrado, porque a distribuição da amostra (como n se aproxima do infinito) é normalmente conhecida. Esta variante do teste é às vezes chamada de Teste de Wald Qui-quadrado para diferenciá-lo do Teste de Wald Log-Linear Qui-quadrado, que é uma variante não paramétrica baseada nos log odds ratios.

Comparação com Outros Testes

O teste de Wald é uma aproximação aproximada do Teste da Razão de Probabilidade. No entanto, você pode executá-lo com um único modelo (o teste LR requer pelo menos dois). Também é mais amplamente aplicável que o LRT: muitas vezes, é possível executar um Wald em situações em que nenhum outro teste pode ser executado.

Para grandes valores de n, o teste de Wald é aproximadamente equivalente ao teste t; ambos os testes rejeitarão os mesmos valores para grandes tamanhos de amostra. Os testes de Wald, LRT e multiplicador Lagrange são todos equivalentes à medida que os tamanhos de amostra se aproximam do infinito (chamados de “assimmptoticamente equivalentes”). Entretanto, amostras de tamanho finito, especialmente amostras menores, provavelmente darão resultados muito diferentes.

Agresti (1990) sugere que você deve usar o LRT em vez do teste de Wald para amostras de tamanho pequeno ou se os parâmetros forem grandes. Um tamanho de amostra “pequena” está abaixo de cerca de 30,

Executar o teste

Ajuda de alimentação com uma pergunta de trabalho de casa? Confira nossa página de tutoria!

A fórmula estatística do Teste de Wald é: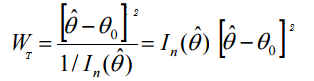

Onde:

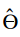• = Estimador de Probabilidade Máxima (EML),
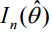• = informação esperada de Fisher (avaliada na EML).

Basicamente, o teste procura por diferenças: Θ0 – Θ. Os passos gerais são:

1. >Inconte o MLE.
2. Inconte as informações esperadas do Fisher.
3. Avalie as informações do Fisher no MLE.

Com a combinação das informações do MLE e do Fisher, o teste de Wald é muito complexo de se trabalhar e normalmente não é calculado à mão. Muitos aplicativos de software podem executar o teste.

• Stata: use o comando teste.
• R: veja as instruções do teste WALD para R (baixe um PDF) da Universidade de Toronto.
• SAS: use a declaração TEST. WALD é o padrão se nenhum teste for especificado.

Referência:
Agresti A. (1990) Análise de dados categóricos. John Wiley and Sons, New York.

——————————————————————————

Need ajuda com um trabalho de casa ou pergunta de teste? Com o Chegg Study, você pode obter soluções passo-a-passo para suas perguntas de um especialista na área. Seus primeiros 30 minutos com um tutor do Chegg são grátis!