
Pitágoras de Samos (c.570-495 BCE)
Biografia – Quem foi Pitágoras
É por vezes afirmado que devemos matemática pura a Pitágoras, e ele é muitas vezes chamado o primeiro matemático “verdadeiro”. Mas, embora a sua contribuição fosse claramente importante, ele continua a ser uma figura controversa.
Ele próprio não deixou escritos matemáticos, e muito do que sabemos sobre o pensamento pitagórico vem-nos dos escritos de Filolau e de outros eruditos pitagóricos posteriores. De fato, não é de forma alguma claro se muitos (ou mesmo qualquer) dos teoremas atribuídos a ele foram de fato resolvidos por Pitágoras pessoalmente ou por seus seguidores.
A escola que ele estabeleceu em Croton no sul da Itália por volta de 530 a.C. era o núcleo de uma seita pitagórica bastante bizarra. Embora o pensamento pitagórico fosse largamente dominado pela matemática, era também profundamente místico, e Pitágoras impôs as suas filosofias quase religiosas, vegetarianismo rigoroso, vida comunitária, ritos secretos e regras estranhas a todos os membros da sua escola (incluindo editos bizarros e aparentemente aleatórios sobre nunca urinar para o sol, nunca casar com uma mulher que usa jóias de ouro, nunca passar um rabo deitado na rua, nunca comer ou mesmo tocar em feijão de fava preto, etc.) .
Os membros foram divididos em “mathematikoi” (ou “aprendizes”), que se estendeu e desenvolveu o trabalho mais matemático e científico que o próprio Pitágoras começou, e os “akousmatikoi” (ou “ouvintes”), que se concentraram nos aspectos mais religiosos e ritualísticos dos seus ensinamentos. Houve sempre um certo atrito entre os dois grupos e, eventualmente, a seita foi apanhada em algumas lutas locais ferozes e acabou por se dispersar. O ressentimento acumulado contra o segredo e exclusividade dos pitágoricos e, em 460 a.C., todos os seus locais de reunião foram queimados e destruídos, com pelo menos 50 membros mortos apenas em Croton.
O ditado dominante da escola de Pitágoras era “Tudo é número” ou “Deus é número”, e os pitágoricos efectivamente praticavam uma espécie de numerologia ou adoração numérica, e consideravam cada número como tendo o seu próprio carácter e significado. Por exemplo, o número um era o gerador de todos os números; dois representavam opinião; três, harmonia; quatro, justiça; cinco, casamento; seis, criação; sete, os sete planetas ou “estrelas errantes”; etc. Números ímpares eram pensados como números femininos e pares como números masculinos.
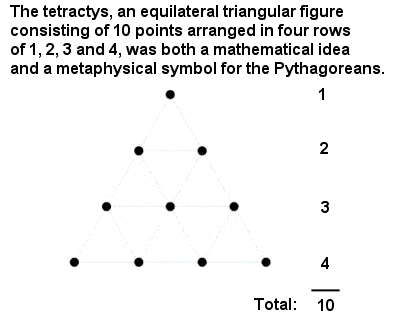
Os Tetractos de Pitágoras
O número mais sagrado de todos era “Tetractos” ou dez, um número triangular composto pela soma de um, dois, três e quatro. É uma grande homenagem aos feitos intelectuais dos pitágoricos que eles deduziram o lugar especial do número 10 de um argumento matemático abstrato e não de algo tão mundano como contar os dedos em duas mãos.
No entanto, Pitágoras e sua escola – assim como um punhado de outros matemáticos da Grécia antiga – foi em grande parte responsável pela introdução de uma matemática mais rigorosa do que a anterior, construindo a partir dos primeiros princípios usando axiomas e lógica. Antes de Pitágoras, por exemplo, a geometria tinha sido apenas uma coleção de regras derivadas por medição empírica.
Pitágoras descobriu que um sistema completo de matemática podia ser construído, onde elementos geométricos correspondiam a números, e onde inteiros e suas proporções eram tudo o que era necessário para estabelecer todo um sistema de lógica e verdade.
O Teorema de Pitágoras
Ele é lembrado principalmente pelo que ficou conhecido como o Teorema de Pitágoras (ou o Teorema de Pitágoras): que, para qualquer triângulo em ângulo recto, o quadrado do comprimento da hipotenusa (o lado mais longo, oposto ao ângulo recto) é igual à soma do quadrado dos outros dois lados (ou “pernas”).
Escrito como uma equação: a2 + b2 = c2.
O que Pitágoras e seus seguidores não perceberam é que isto também funciona para qualquer forma: assim, a área de um pentágono na hipotenusa é igual à soma dos pentágonos dos outros dois lados, como faz para um semicírculo ou qualquer outro regular (ou mesmo irregular( forma.
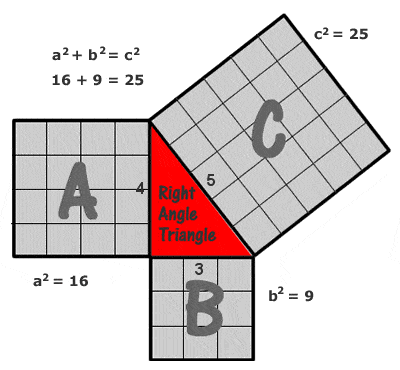
Teorema de Pitágoras
O exemplo mais simples e mais comumente citado de um triângulo pitágoro é um com lados de 3, 4 e 5 unidades (32 + 42 = 52, como pode ser visto desenhando uma grade de quadrados unitários em cada lado como no diagrama à direita), mas há um número potencialmente infinito de outros “triplos pitagóricos” inteiros, começando por (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), etc. Deve-se notar, porém, que (6, 8, 10) não é o que se conhece como um triplo pitagórico “primitivo”, pois é apenas um múltiplo de (3, 4, 5).
Theorem de Pitágoras e as propriedades dos triângulos retos parecem ser o desenvolvimento matemático mais antigo e difundido após a aritmética e geometria básicas, e foi abordado em alguns dos textos matemáticos mais antigos da Babilônia e do Egito, datando de mais de mil anos antes. Uma das provas mais simples vem da China antiga, e provavelmente data de muito antes do nascimento de Pitágoras. Foi Pitágoras, porém, quem deu ao teorema a sua forma definitiva, embora não esteja claro se o próprio Pitágoras o provou definitivamente ou apenas o descreveu. De qualquer forma, tornou-se um dos mais conhecidos de todos os teoremas matemáticos, e existem hoje até 400 provas diferentes, algumas geométricas, algumas algébricas, algumas envolvendo equações diferenciais avançadas, etc.
Tornou-se evidente, no entanto, que também eram possíveis soluções não inteiras, de modo que um triângulo isósceles com lados 1, 1 e √2, por exemplo, também tem um ângulo recto, como os babilónios tinham descoberto séculos antes. No entanto, quando o estudante de Pitágoras Hippasus tentou calcular o valor de √2, descobriu que não era possível expressá-lo como uma fração, indicando assim a existência potencial de todo um novo mundo de números, os números irracionais (números que não podem ser expressos como simples frações de números inteiros). Esta descoberta destruiu bastante o elegante mundo matemático construído por Pitágoras e seus seguidores, e a existência de um número que não podia ser expresso como a proporção de duas das criações de Deus (que é como eles pensavam dos inteiros) prejudicou todo o sistema de crenças do culto.
Pobre Hippasus foi aparentemente afogado pelos secretos pitagóricos para transmitir esta importante descoberta para o mundo exterior. Mas a substituição da idéia da divindade dos inteiros pelo conceito mais rico do continuum, foi um desenvolvimento essencial na matemática. Marcou o nascimento real da geometria grega, que trata de linhas, planos e ângulos, todos contínuos e não discretos.
Entre as suas outras realizações em geometria, Pitágoras (ou pelo menos os seus seguidores, os pitagóricos) também percebeu que a soma dos ângulos de um triângulo é igual a dois ângulos rectos (180°), e provavelmente também a generalização que afirma que a soma dos ângulos interiores de um polígono com n lados é igual a (2n – 4) ângulos rectos, e que a soma dos seus ângulos exteriores é igual a 4 ângulos rectos. Eles foram capazes de construir figuras de uma determinada área, e usar álgebra geométrica simples, por exemplo para resolver equações como a(a – x) = x2 por meios geométricos.
Os pitagóricos também estabeleceram os fundamentos da teoria dos números, com suas investigações de números triangulares, quadrados e também perfeitos (números que são a soma de seus divisores). Eles descobriram várias novas propriedades dos números quadrados, tais como que o quadrado de um número n é igual à soma dos primeiros números n ímpares (ex. 42 = 16 = 1 + 3 + 5 + 7). Eles também descobriram pelo menos o primeiro par de números amigáveis, 220 e 284 (números amigáveis são pares de números para os quais a soma dos divisores de um número é igual ao outro número, por exemplo, os divisores próprios de 220 são 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, dos quais a soma é 284; e os divisores próprios de 284 são 1, 2, 4, 71 e 142, dos quais a soma é 220).
Teoria da música
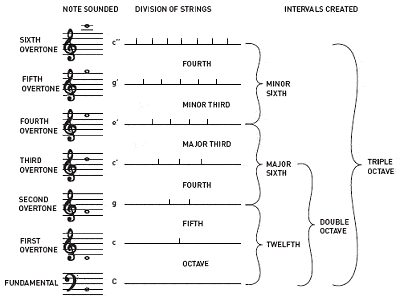
Pitágoras é creditada com a descoberta das relações entre as notas musicais harmoniosas
Pitágoras é também creditada com a descoberta de que os intervalos entre notas musicais harmoniosas têm sempre relações numéricas inteiras. Por exemplo, tocar metade de uma corda de guitarra dá a mesma nota que a corda aberta, mas uma oitava mais alta; um terço de um comprimento dá uma nota diferente mas harmoniosa; etc.
Non-whole number ratios, por outro lado, tendem a dar sons dissonantes. Desta forma, Pitágoras descreveu os quatro primeiros sobre-tons que criam os intervalos comuns que se tornaram os principais blocos de construção da harmonia musical: a oitava (1:1), a quinta perfeita (3:2), a quarta perfeita (4:3) e a terceira maior (5:4). A forma mais antiga de afinar a escala cromática de 12 notas é conhecida como afinação pitagórica, e é baseada numa pilha de quintos perfeitos, cada um afinado na razão 3:2.
A mística Pitágoras ficou tão excitada com esta descoberta que se convenceu que todo o universo era baseado em números, e que os planetas e estrelas se moviam de acordo com equações matemáticas, que correspondiam a notas musicais, e assim produziu uma espécie de sinfonia, a “Musical Universalis” ou “Music of the Spheres”.
| << De volta à Matemática Grega | Em frente a Platão >> |
