Sabemos como encontrar a raiz quadrada de qualquer número real positivo. De forma semelhante, podemos encontrar a raiz quadrada de um número negativo. A diferença é que a raiz não é real. Se o valor no radicand é negativo, diz-se que a raiz é um número imaginário. O número imaginário i é definido como a raiz quadrada do negativo 1.
Então, usando propriedades dos radicais,
Podemos escrever a raiz quadrada de qualquer número negativo como um múltiplo de i. Considere a raiz quadrada de -25.
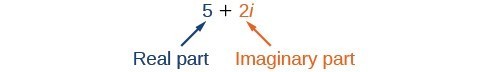
Figure 1
Um número complexo é a soma de um número real e um número imaginário. Um número complexo é expresso na forma padrão quando escrito a + bi onde a é a parte real e bi é a parte imaginária. Por exemplo, 5+2i é um número complexo. Então, também é 3+4\sqrt{3}i9640>
Números imaginários são distinguidos dos números reais porque um número imaginário ao quadrado produz um número real negativo. Lembre-se, quando um número real positivo é ao quadrado, o resultado é um número real positivo e quando um número real negativo é ao quadrado, novamente, o resultado é um número real positivo. Números complexos são uma combinação de números reais e imaginários.
A General Note: Imaginary and Complex Numbers
A complex number is a number of the form a+bi\\\ where
- a is the real part of the complex number.
- bi é a parte imaginária do número complexo.
Se b=0\\\\, então a+bi\\\ é um número real. Se a=0\\\ e b não for igual a 0, o número complexo é chamado de número imaginário. Um número imaginário é uma raiz par de um número negativo.
Como fazer: Dado um número imaginário, expresse-o na forma padrão.
- Escreva {a}sqrt{a}sqrt{-1}.
- Expresse {-1}sqrt{-1}como i.
- Escreva {a}cdot i na forma mais simples.
Exemplo 1: Expressar um número imaginário em forma padrão
Expressar \sqrt{-9}\sqrt{-9}} em forma padrão.
Solução
\sqrt{-9}=\sqrt{-9}=\sqrt{-1}=3i{-1}>
Em formulário padrão, este é 0+3i{\sqrt{-9}}.
Try It 1
Express \sqrt{-24}\sqrt{-24}\sqrt{\sqrt{-24}\sqrt{\sqrt{-24}\sqrt{-24}\sqrt{-24}\sqrt{-24}\sqrt{-24}\sqrt{-9}\sqrt{-9}\sqrt{-9}\sqrt
