Nesta seção, vamos nos familiarizar com as operações e notações do conjunto, para que possamos aplicar estes conceitos tanto para a contagem como para os problemas de probabilidade. Começamos por definir alguns termos.
Um conjunto é uma coleção de objetos, e seus membros são chamados os elementos do conjunto. Nós nomeamos o conjunto usando letras maiúsculas, e colocamos seus membros entre parênteses curvos. Suponhamos que precisamos listar os membros do clube de xadrez. Usamos a seguinte notação de conjunto.
C ={Ken, Bob, Tran, Shanti, Eric}
Um conjunto que não tem membros é chamado de conjunto vazio. O conjunto vazio é denotado pelo símbolo Ø.
Dois conjuntos são iguais se tiverem os mesmos elementos.
Um conjunto A é um subconjunto de um conjunto B se cada membro de A também for membro de B.
Suponha C = {Al, Bob, Chris, David, Ed} e A = {Bob, David}. Então A é um subconjunto de C, escrito como 
.
Cada conjunto é um subconjunto de si mesmo, e o conjunto vazio é um subconjunto de cada conjunto.
União de Dois Conjuntos
Deixe A e B serem dois conjuntos, então a união de A e B, escrito como 
, é o conjunto de todos os elementos que estão ou em A ou em B, ou em ambos A e B.
Intersecção de dois conjuntos
Deixe A e B serem dois conjuntos, depois a intersecção de A e B, escrita como 
, é o conjunto de todos os elementos que são comuns aos dois conjuntos A e B.
Um conjunto universal U é o conjunto constituído por todos os elementos em consideração.
Complemento de um conjunto
Deixe A ser qualquer conjunto, então o complemento do conjunto A, escrito como 
, é o conjunto composto por elementos do conjunto universal U que não estão em A.
Conjuntos de conjuntos conjuntos
Dois conjuntos A e B são chamados conjuntos de conjuntos de conjuntos de conjuntos de conjuntos de conjuntos de conjuntos de conjuntos de conjuntos, se a sua intersecção for um conjunto vazio.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {laranja, verde, anil, violeta} Para conseguir uma melhor compreensão, suponhamos que o conjunto universal U representa as cores do espectro, e P as cores primárias, então representa aquelas cores do espectro que não são cores primárias.
.
= {vermelho, amarelo, azul, verde}
= {laranja, anil, violeta}
= {vermelho, amarelo, azul, violeta} = {violeta}Venn Diagramas
Agora usamos diagramas Venn para ilustrar as relações entre conjuntos. No final do século XIX, um lógico inglês chamado John Venn desenvolveu um método para representar as relações entre conjuntos. Ele representava essas relações usando diagramas, que agora são conhecidos como diagramas Venn. Um diagrama Venn representa um conjunto como o interior de um círculo. Muitas vezes dois ou mais círculos estão fechados num rectângulo onde o rectângulo representa o conjunto universal. Para visualizar uma intersecção ou união de um conjunto é fácil. Nesta seção, vamos usar principalmente os diagramas Venn para classificar várias populações e contar objetos.
|
(a) |
(b) |
(c) |
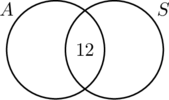
Porque 30 pessoas conduziam carros com transmissões automáticas, o círculo A deve conter 30 elementos. Isto significa x + 12 = 30, ou x = 18. Da mesma forma, como 20 pessoas conduziram carros com transmissões padrão, o círculo B deve conter 20 elementos, ou y +12 = 20 que por sua vez faz y = 8,
Agora toda a informação é classificada, é fácil de ler a partir do diagrama que 18 pessoas conduziram carros com transmissões automáticas apenas, 12 pessoas conduziram ambos os tipos de carros, e 8 conduziram carros com transmissões padrão apenas. Portanto, 18 + 12 + 8 = 38 pessoas participaram da pesquisa.
|
(a) |
(b) |
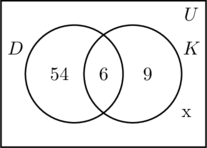
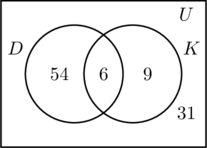
Preenchemos as três regiões associadas com os conjuntos D e K da mesma forma que antes. Como 100 pessoas participaram na pesquisa, o retângulo que representa o conjunto universal U deve conter 100 objetos. Que x representem as pessoas do conjunto universal que não estão nem no conjunto D nem em K. Isto significa 54 + 6 + 9 + x = 100, ou x = 31,
Por isso, há 31 pessoas na pesquisa que não visitaram nenhum lugar.
- 50 jog, 30 nadar e 35 ciclo
- 14 jog e nadar
- 7 nadar e ciclo
- 9 jog e ciclo
- 3 pessoas participam nas três actividades
Solução
|
(a) |
(b) |
(c) |
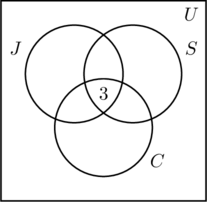
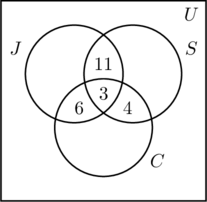
Pomos um 3 na região mais interna da Figura (a) porque representa o número de pessoas que participam nas três actividades. A seguir calculamos x, y e z.
- Desde 14 pessoas jogam e nadam, x +3 = 14, ou x = 11.
- O facto de 9 pessoas jogarem e nadarem de bicicleta resulta em y + 3 = 9, ou y = 6.
- Desde 7 pessoas a nadar e a andar de bicicleta, z + 3 = 7, ou z = 4.
- Esta informação está representada na Figura (b).
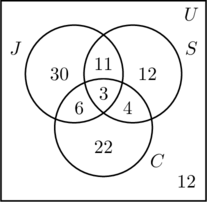
- Desde 50 pessoas jogam, m + 11 + 6 + 3 = 50, ou m = 30.
- 30 pessoas nadam, portanto, n + 11 + 4 + 3 = 30, ou n = 12,
- 35 pessoas pedalam, portanto, p + 6 + 4 + 3 = 35, ou p = 22.
- Adicionando todas as entradas nos três conjuntos, obtemos uma soma de 88. Como foram inquiridas 100 pessoas, o número dentro do conjunto universal mas fora de todos os três conjuntos é 100 – 88, ou 12.
- Na Figura (c), a informação é ordenada, e as perguntas podem ser prontamente respondidas.
Perguntas práticas
1. Que o conjunto Universal U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h}, e W = {a, c, e, g, i}. Liste os membros dos seguintes conjuntos:
a. 
b. 
2. Considere os seguintes conjuntos: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, Influenza, Norovirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella}, e C = {SARS, Listeria, Tuberculosis, H5N1, Salmonella, HIV, COVID-19}. Liste os membros dos seguintes conjuntos:
a. 
b. 
3. Uma pesquisa com atletas revelou que para suas pequenas dores, 30 usavam aspirina, 50 ibuprofeno, e 15 usavam ambos. Todos os atletas pesquisados usaram pelo menos um dos dois analgésicos. Quantos atletas foram pesquisados?
4. Um estudo com 150 alunos do ensino médio revelou que 25 relataram ter sofrido uma concussão ou lesão na cabeça, 52 relataram doença mental, e 15 relataram ambos os resultados. Quantos alunos não relataram nenhum dos resultados?
5. Uma pesquisa com 100 estudantes da Ryerson University descobriu que 50 assinam o Netflix, 40 assinam o Amazon Prime, e 30 assinam o Disney+. Destes, 15 são assinantes do Netflix e do Amazon Prime, 10 do Amazon Prime e Disney+, 10 do Netflix e Disney+, e 5 têm os três serviços de assinatura. Desenhe um diagrama Venn e determine o seguinte:
a. O número de alunos assinantes do Amazon Prime mas não os outros dois serviços de streaming.
b. O número de alunos assinantes do Netflix ou Amazon Prime mas não da Disney+.
c. O número de alunos que não assinam nenhum desses serviços.