Grupo

Um grupo é um conjunto finito ou infinito de elementos juntamente com uma operação binária (chamada operação de grupo) que juntos satisfazem as quatro propriedades fundamentais de fechamento, associatividade, a propriedade de identidade e a propriedade inversa. A operação com respeito à qual um grupo é definido é freqüentemente chamada de “operação de grupo”, e um conjunto é dito ser um grupo “sob” esta operação. Elementos , , , … com operação binária entre e denoted formam um grupo se

1. Fechamento: Se e são dois elementos em , então o produto também está em .

2>. Associatividade: A multiplicação definida é associativa, ou seja, para todos , .

3. Identidade: Existe um elemento de identidade (também conhecido como 1, , ou ) tal que para cada elemento .

4. Inverso: Deve haver um inverso (também conhecido como recíproco) de cada elemento. Portanto, para cada elemento de , o conjunto contém um elemento tal que .

Um grupo é um monóide, cada um dos elementos é invertível.

Um grupo deve conter pelo menos um elemento, com o único (até isomorfismo) grupo de um elemento, conhecido como grupo trivial.

O estudo dos grupos é conhecido como teoria dos grupos. Se houver um número finito de elementos, o grupo é chamado de grupo finito e o número de elementos é chamado de ordem de grupo do grupo. Um subconjunto de um grupo que é fechado sob a operação de grupo e a operação inversa é chamada de subgrupo. Subgrupos também são grupos, e muitos grupos comumente encontrados são na verdade subgrupos especiais de algum grupo maior mais geral.

Um exemplo básico de um grupo finito é o grupo simétrico , que é o grupo de permutações (ou “sob permutação”) de objetos. O grupo infinito mais simples é o conjunto de números inteiros sob adição habitual. Para grupos contínuos, pode-se considerar os números reais ou o conjunto de matrizes inversíveis. Estes dois últimos são exemplos de grupos de mentira.

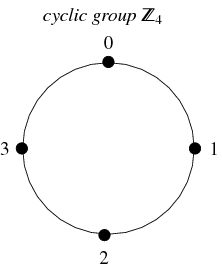
Um tipo muito comum de grupo são os grupos cíclicos. Este grupo é isomórfico para o grupo de inteiros (modulo ), é denotado , , ou , e é definido para cada número inteiro . É fechado sob adição, associativo, e tem inversos únicos. Os números de 0 a representam seus elementos, com o elemento de identidade representado por 0, e o inverso de é representado por .

Um mapa entre dois grupos que preserva a identidade e a operação do grupo é chamado de homomorfismo. Se um homomorfismo tem um inverso que também é um homomorfismo, então é chamado de isomorfismo e os dois grupos são chamados de isomorfismo. Dois grupos que são isomórficos um para o outro são considerados “os mesmos” quando vistos como grupos abstratos. Por exemplo, o grupo de rotações de um quadrado, ilustrado abaixo, é o grupo cíclico .

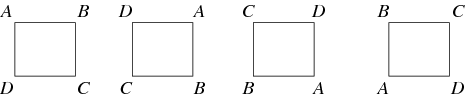
Em geral, uma ação de grupo é quando um grupo atua sobre um conjunto, permutando seus elementos, de modo que o mapa do grupo para o grupo permutação do conjunto é um homomorfismo. Por exemplo, as rotações de um quadrado são um subgrupo das permutações de seus cantos. Uma importante ação de grupo para qualquer grupo é a sua ação sobre si mesma por conjugação. Estes são apenas alguns dos possíveis automorfismos de grupo. Outro tipo importante de ação grupal é uma representação grupal, onde o grupo atua sobre um espaço vetorial por mapas lineares inversíveis. Quando o campo do espaço vectorial são os números complexos, por vezes uma representação é chamada módulo CG.

Acções de grupo, e em particular representações, são muito importantes em aplicações, não só para agrupar teoria, mas também para a física e química. Uma vez que um grupo pode ser pensado como um objeto matemático abstrato, o mesmo grupo pode surgir em contextos diferentes. Portanto, é útil pensar em uma representação do grupo como uma encarnação particular do grupo, que também pode ter outras representações. Uma representação irredutível de um grupo é uma representação para a qual não existe uma transformação unitária que transformará a matriz de representação em forma de bloco em diagonal. As representações irredutíveis têm uma série de propriedades notáveis, como formalizadas no teorema da ortogonalidade do grupo.