- Objetivos de aprendizado
- Exemplo 1. Calculando a Energia Fóton e o Efeito Fotoelétrico: A Violet Light
- Estratégia
- Solução para a Parte 1
- Solução para a Parte 2
- Discussão
- PhET Explorations: Efeito Fotoelétrico
- Section Summary
- Perguntas conceptuais
- Problemas & Exercícios
- Glossary
- Soluções selecionadas para problemas & Exercícios
Objetivos de aprendizado
Ao final desta seção, você poderá:
- Descrever uma experiência típica de efeito fotoelétrico.
- Determinar a energia cinética máxima dos fotoelétrons ejetados por fótons de uma energia ou comprimento de onda, quando dada a energia cinética máxima dos fotoelétrons para uma energia ou comprimento de onda diferente.
Quando a luz atinge materiais, ela pode ejetar elétrons deles. Isto é chamado efeito fotoelétrico, significando que a luz (foto) produz eletricidade. Um uso comum do efeito fotoelétrico é em medidores de luz, como aqueles que ajustam a íris automática em vários tipos de câmeras. De forma semelhante, outro uso é nas células solares, como provavelmente tem na sua calculadora ou viu no topo de um telhado ou numa placa de beira de estrada. Estas fazem uso do efeito fotoeléctrico para converter a luz em electricidade, para a utilização de diferentes dispositivos.

Figure 1. O efeito fotoelétrico pode ser observado permitindo que a luz caia sobre a placa metálica neste tubo evacuado. Os elétrons ejetados pela luz são coletados no fio coletor e medidos como uma corrente. Uma tensão retardada entre o fio colector e a placa pode então ser ajustada de modo a determinar a energia dos electrões ejectados. Por exemplo, se for suficientemente negativo, nenhum elétron alcançará o fio. (crédito: P.P. Urone)
Este efeito é conhecido há mais de um século e pode ser estudado usando um dispositivo como o mostrado na Figura 1. Esta figura mostra um tubo evacuado com uma placa metálica e um fio colector que estão ligados por uma fonte de tensão variável, com o colector mais negativo do que a placa. Quando a luz (ou outra radiação EM) atinge a placa no tubo evacuado, ela pode ejetar elétrons. Se os elétrons tiverem energia em volts de elétrons (eV) maior do que a diferença de potencial entre a placa e o fio em volts, alguns elétrons serão coletados no fio. Como a energia dos electrões em eV é eV, onde q é a carga de electrões e V é a diferença de potencial, a energia dos electrões pode ser medida ajustando a tensão de retardamento entre o fio e a placa. A tensão que impede que os electrões cheguem ao fio é igual à energia em eV. Por exemplo, se -3,00 V mal pára os elétrons, sua energia é de 3,00 eV. O número de elétrons ejetados pode ser determinado medindo a corrente entre o fio e a placa. Quanto mais luz, mais elétrons; um pequeno circuito permite que este dispositivo seja usado como um medidor de luz.
O que é realmente importante sobre o efeito fotoelétrico é o que Albert Einstein deduziu dele. Einstein percebeu que havia várias características do efeito fotoelétrico que só poderiam ser explicadas se a própria radiação EM fosse quantificada: o fluxo aparentemente contínuo de energia em uma onda EM é na verdade composto de quanta energia chamada de fótons. Em sua explicação do efeito fotoelétrico, Einstein definiu uma unidade quantificada ou quantum de energia EM, que agora chamamos de fóton, com uma energia proporcional à freqüência da radiação EM. Na forma de equação, a energia do fotão é E = hf, onde E é a energia de um fotão de frequência f e h é a constante de Planck. Esta ideia revolucionária parece semelhante à quantização dos estados de energia dos osciladores de corpo negro de Planck, mas é bastante diferente. É a própria quantização da radiação EM. As ondas EM são compostas de fótons e não são ondas lisas contínuas, como descrito nos capítulos anteriores sobre ótica. Sua energia é absorvida e emitida em grumos, não continuamente. Isto é exatamente consistente com a quantização dos níveis de energia dos osciladores de corpo negro do Planck, já que estes osciladores aumentam e diminuem sua energia em etapas de hf absorvendo e emitindo fótons com E = hf. Não observamos isto com os olhos, porque há tantos fotões em fontes de luz comuns que os fotões individuais passam despercebidos. (Ver Figura 2.) A secção seguinte do texto (Energias Fotónicas e o Espectro Electromagnético) é dedicada a uma discussão sobre os fotões e algumas das suas características e implicações. Por enquanto, vamos usar o conceito de fótons para explicar o efeito fotoelétrico, como Einstein fez.
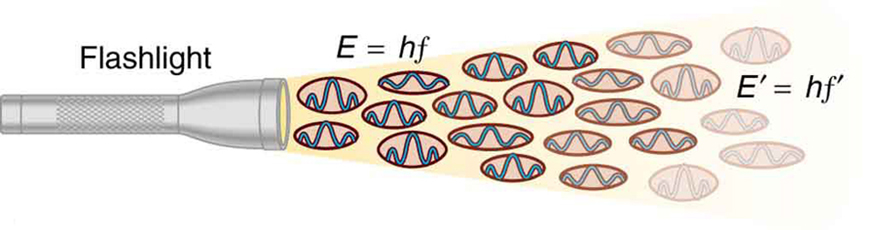
Figure 2. Uma onda EM de freqüência f é composta de fótons, ou quanta individual de radiação EM. A energia de cada fóton é E = hf, onde h é a constante de Planck e f é a freqüência da radiação EM. Maior intensidade significa mais fótons por unidade de área. A lanterna emite um grande número de fótons de muitas frequências diferentes, portanto outros têm energia E′ = hf′, e assim por diante.
O efeito fotoelétrico tem as propriedades discutidas abaixo. Todas estas propriedades são consistentes com a idéia de que fótons individuais de radiação EM são absorvidos por elétrons individuais em um material, com o elétron ganhando a energia do fóton. Algumas destas propriedades são inconsistentes com a idéia de que a radiação EM é uma simples onda. Para simplificar, vamos considerar o que acontece com a radiação monocromática EM na qual todos os fótons têm a mesma energia hf.
- Se variarmos a freqüência da radiação EM caindo sobre um material, encontramos o seguinte: Para um determinado material, existe uma frequência limite f0 para a radiação EM abaixo da qual não são ejectados electrões, independentemente da intensidade. Os fótons individuais interagem com os elétrons individuais. Assim, se a energia do fóton for muito pequena para quebrar um elétron, nenhum elétron será ejetado. Se a radiação EM fosse uma onda simples, energia suficiente poderia ser obtida aumentando a intensidade.
- Uma vez que a radiação EM cai sobre um material, os elétrons são ejetados sem demora. Assim que um fotão individual de frequência suficientemente alta é absorvido por um electrão individual, o electrão é ejectado. Se a radiação EM fosse uma onda simples, seriam necessários vários minutos para que fosse depositada energia suficiente na superfície metálica para ejetar um elétron.
- O número de elétrons ejetados por unidade de tempo é proporcional à intensidade da radiação EM e a nenhuma outra característica. A radiação EM de alta intensidade consiste em um grande número de fótons por unidade de área, com todos os fótons tendo a mesma energia característica hf.
- Se variarmos a intensidade da radiação EM e medirmos a energia dos elétrons ejetados, encontramos o seguinte: A energia cinética máxima dos elétrons ejetados é independente da intensidade da radiação EM. Como há tantos elétrons em um material, é extremamente improvável que dois fótons interajam com o mesmo elétron ao mesmo tempo, aumentando assim a energia dada a ele. Em vez disso (como foi observado no ponto 3 acima), o aumento da intensidade resulta em mais elétrons com a mesma energia sendo ejetados. Se a radiação EM fosse uma onda simples, uma maior intensidade poderia dar mais energia e elétrons de maior energia seriam ejetados.
- A energia cinética de um elétron ejetado é igual à energia do fóton menos a energia de ligação do elétron no material específico. Um fóton individual pode dar toda a sua energia a um electrão. A energia do fóton é parcialmente utilizada para separar o electrão do material. O restante vai para a energia cinética do elétron ejetado. Em forma de equação, esta é dada por KEe = hf – BE, onde KEe é a energia cinética máxima do elétron ejetado, hf é a energia do fóton, e BE é a energia de ligação do elétron ao material em particular. (BE é por vezes chamada a função de trabalho do material.) Esta equação, devido a Einstein em 1905, explica quantitativamente as propriedades do efeito fotoeléctrico. Um fotão individual de radiação EM (não vem de outra forma) interage com um elétron individual, fornecendo energia suficiente, BE, para quebrá-lo, com o restante indo para a energia cinética. A energia de ligação é BE = hf0, onde f0 é a frequência limite para o material em particular. A Figura 3 mostra um gráfico de KEe máximo versus a freqüência de radiação EM incidente caindo sobre um determinado material.
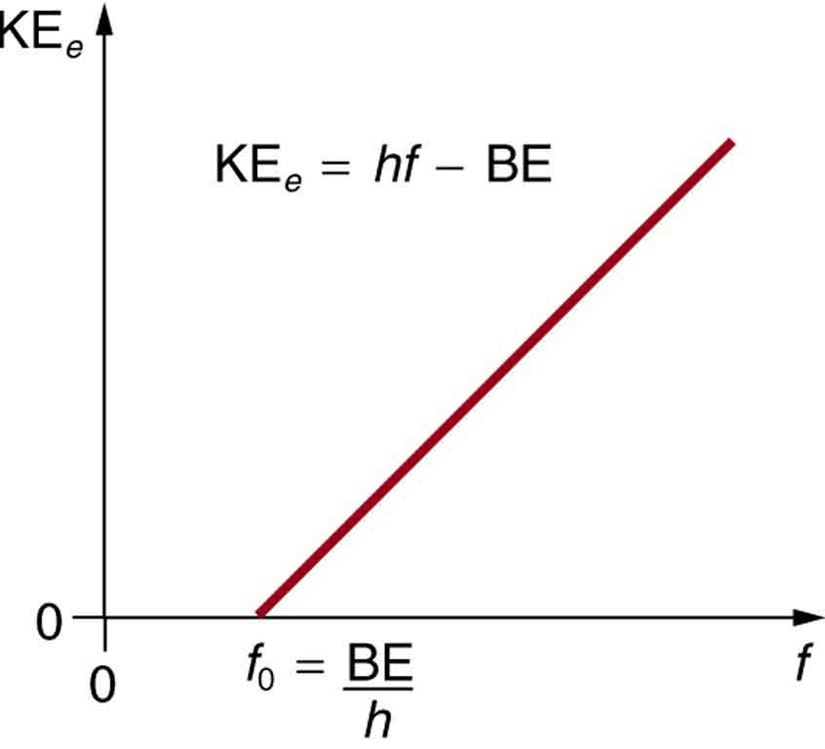
Figure 3. Efeito fotoelétrico. Um gráfico da energia cinética de um elétron ejetado, KEe, versus a freqüência da radiação EM que incide sobre um determinado material. Existe uma frequência limite abaixo da qual não são ejectados electrões, porque o fotão individual que interage com um electrão individual não tem energia suficiente para o quebrar. Acima do limiar de energia, a KEe aumenta linearmente com f, consistente com a KEe = hf – BE. A inclinação desta linha é h – os dados podem ser usados para determinar experimentalmente a constante de Planck. Einstein deu a primeira explicação bem sucedida de tais dados ao propor a idéia de fotões-quanta da radiação EM.
A idéia de Einstein de que a radiação EM é quantificada foi crucial para o início da mecânica quântica. É um conceito muito mais geral do que a sua explicação do efeito fotoelétrico poderia implicar. Toda radiação EM pode também ser modelada na forma de fótons, e as características da radiação EM são inteiramente consistentes com este fato. (Como veremos na próxima seção, muitos aspectos da radiação EM, como os perigos da radiação ultravioleta (UV), podem ser explicados apenas pelas propriedades dos fótons). Mais famoso pela relatividade moderna, Einstein plantou uma semente importante para a mecânica quântica em 1905, no mesmo ano em que publicou seu primeiro trabalho sobre relatividade especial. Sua explicação sobre o efeito fotoelétrico foi a base para o Prêmio Nobel que lhe foi concedido em 1921. Embora suas outras contribuições para a física teórica também foram notadas nesse prêmio, a relatividade especial e geral não foi totalmente reconhecida, apesar de ter sido parcialmente verificada por experiência até 1921. Embora heróico, este grande homem nunca recebeu o reconhecimento Nobel pela sua relatividade de trabalho mais famosa.
Exemplo 1. Calculando a Energia Fóton e o Efeito Fotoelétrico: A Violet Light
1. Qual é a energia em joules e volts de electrões de um fotão de luz violeta de 420 nm?
2. Qual é a energia cinética máxima dos electrões ejectados do cálcio por luz violeta de 420 nm, dado que a energia de ligação (ou função de trabalho) dos electrões para o cálcio metálico é de 2,71 eV?
Estratégia
Para resolver a Parte 1, note que a energia de um fotão é dada por E = hf. Para a Parte 2, uma vez calculada a energia do fotão, é uma aplicação directa de KEe = hf – BE para encontrar a energia cinética máxima do electrão ejectado, uma vez que BE é dado.
Solução para a Parte 1
Energia do fotão é dada por E = hf.
Desde que nos é dado o comprimento de onda e não a frequência, resolvemos a relação familiar c = fλ para a frequência, produzindo f=\frac{c}{\lambda}\.
Combinando estas duas equações obtém-se a relação útil E=\frac{hc}{\lambda}.
Agora substituindo os rendimentos de valores conhecidos
>displaystyle{E}=frac{esquerda(6.63}vezes10^{-34}texto{ J}cdot{squerda){esquerda(3.00 vezes10{8}texto{m/s}{420 vezes10{-9}texto{ m}=4,74 vezes10{-19}texto{ J
Convertendo para eV, a energia do fotão é
>esquerda{E}=esquerda(4.47 vezes10 ^{-19}text{ J}}frac{1}text{ eV}{1.6 ^{-19}text{ J}}=2.96 ^{{{19}text{ eV}
Solução para a Parte 2
Encontrar a energia cinética do elétron ejetado é agora uma simples aplicação da equação KEe = hf – BE. Substituindo a energia do fotão e a energia de ligação KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV.
Discussão
A energia deste fotão de 420 nm de luz violeta é uma fracção minúscula de um joule, e por isso não é de admirar que um único fotão seja difícil para nós sentir directamente – os humanos estão mais sintonizados com as energias na ordem dos joules. Mas olhando para a energia em volts de elétron, podemos ver que este fóton tem energia suficiente para afetar átomos e moléculas. Uma molécula de DNA pode ser quebrada com cerca de 1 eV de energia, por exemplo, e as energias atômicas e moleculares típicas estão na ordem de eV, de modo que o fóton UV neste exemplo poderia ter efeitos biológicos. O elétron ejetado (chamado fotoelétron) tem uma energia bastante baixa, e não viajaria muito longe, exceto no vácuo. O elétron seria parado por um potencial retardador de apenas 0,26 eV. Na verdade, se o comprimento de onda do fotão fosse maior e a sua energia inferior a 2,71 eV, então a fórmula daria uma energia cinética negativa, uma impossibilidade. Isto significa simplesmente que os fotões de 420 nm com a sua energia de 2,96-eV não estão muito acima do limiar de frequência. Você pode mostrar para si mesmo que o comprimento de onda do limiar é 459 nm (luz azul). Isto significa que se o metal de cálcio for usado num medidor de luz, o medidor será insensível a comprimentos de onda mais longos do que os da luz azul. Tal medidor de luz seria completamente insensível à luz vermelha, por exemplo.
PhET Explorations: Efeito Fotoelétrico
Veja como a luz faz com que os elétrons saiam de um alvo metálico, e recrie a experiência que desovou o campo da mecânica quântica.

Clique para baixar a simulação. Execute usando Java.
Section Summary
- O efeito fotoelétrico é o processo no qual a radiação EM ejeta elétrons de um material.
- Einstein propôs que os fótons fossem quanta da radiação EM tendo energia E = hf, onde f é a freqüência da radiação.
- Toda radiação EM é composta de fótons. Como Einstein explicou, todas as características do efeito fotoelétrico são devidas à interação de fótons individuais com elétrons individuais.
- A energia cinética máxima KEe dos elétrons ejetados (fotoelétrons) é dada por KEe = hf – BE, onde hf é a energia do fóton e BE é a energia de ligação (ou função de trabalho) do elétron ao material em particular.
Perguntas conceptuais
- É a luz visível o único tipo de radiação EM que pode causar o efeito fotoeléctrico?
- Que aspectos do efeito fotoeléctrico não podem ser explicados sem os fotões? O que pode ser explicado sem os fótons? Estes últimos são inconsistentes com a existência de fotões?
- O efeito fotoeléctrico é uma consequência directa do carácter de onda da radiação EM ou do carácter de partícula da radiação EM? Explique brevemente.
- Os isoladores (não metálicos) têm um BE superior aos metais, e é mais difícil para os fótons ejetar os elétrons dos isoladores. Discuta como isso se relaciona com as cargas livres em metais que os tornam bons condutores.
- Se você pegar e agitar um pedaço de metal que tenha elétrons livres para se mover como uma corrente, nenhum elétron cairá fora. No entanto, se você aquecer o metal, os elétrons podem ser fervidos. Explique esses dois fatos, pois eles estão relacionados à quantidade e distribuição de energia envolvida no agitar do objeto em comparação com o aquecimento.
Problemas & Exercícios
- Qual é a radiação EM de maior comprimento de onda que pode ejetar um fotoelétron a partir da prata, dado que a energia de ligação é 4,73 eV? Isto está no alcance visível?
- Ponhamos o fotão de maior comprimento de onda que pode ejectar um electrão de potássio, dado que a energia de ligação é 2,24 eV. É esta radiação EM visível?
- Qual é a energia de ligação em eV dos electrões em magnésio, se o fotão de maior comprimento de onda que pode ejectar electrões for 337 nm?
- Calcular a energia de ligação em eV dos electrões em alumínio, se o fotão de maior comprimento de onda que pode ejectar electrões for 304 nm.
- Qual é a energia cinética máxima em eV de elétrons ejetados do metal de sódio pela radiação EM de 450 nm, dado que a energia de ligação é 2,28 eV?
- A radiação UV com comprimento de onda de 120 nm cai sobre o metal dourado, ao qual os elétrons são ligados por 4,82 eV. Qual é a energia cinética máxima dos fotoelétrons ejetados?
- Luz violeta de comprimento de onda 400 nm ejeta elétrons com uma energia cinética máxima de 0,860 eV do metal sódio. Qual é a energia de ligação dos electrões ao metal sódio?
- A radiação UV com um comprimento de onda de 300 nm cai sobre o metal urânio, ejectando 0,500-eV electrões. Qual é a energia de ligação dos elétrons ao metal urânio?
- (a) Qual é o comprimento de onda da radiação EM que ejeta 2,00-eV elétrons do metal cálcio, dado que a energia de ligação é 2,71 eV? (b) Que tipo de radiação EM é esta?
- Inconte o comprimento de onda dos fótons que ejetam 0,100-eV elétrons de potássio, dado que a energia de ligação é 2,24 eV. Estes fotões são visíveis?
- Qual é a velocidade máxima de projecção de electrões de um material por fotões de 80 nm, se forem ligados ao material por 4,73 eV?
- Fotoelectrões de um material com uma energia de ligação de 2,71 eV são ejectados por fotões de 420 nm. Uma vez ejectados, quanto tempo leva estes electrões a viajar 2,50 cm até um dispositivo de detecção?
- Um laser com uma potência de 2,00 mW a um comprimento de onda de 400 nm é projectado sobre metal de cálcio. (a) Quantos elétrons por segundo são ejetados? (b) Que potência é transportada pelos elétrons, dado que a energia de ligação é 2,71 eV?
- (a) Calcular o número de fotoelétrons por segundo ejetados de uma área de 1,00-mm 2 de metal de sódio por 500 nm de radiação EM com uma intensidade de 1,30 kW/m2 (a intensidade da luz solar acima da atmosfera da Terra). (b) Dado que a energia de ligação é 2,28 eV, que potência é transportada pelos elétrons? (c) Os electrões transportam menos energia do que a trazida pelos fotões. Para onde vai a outra energia? Como pode ser recuperada?
- Resultados pouco razoáveis. A luz vermelha com um comprimento de onda de 700 nm é projectada sobre metal magnésio ao qual os electrões estão ligados por 3,68 eV. (a) Use KEe = hf – BE para calcular a energia cinética dos elétrons ejetados. (b) O que há de irrazoável neste resultado? (c) Que suposições não são razoáveis ou inconsistentes?
- Resultados não razoáveis. (a) Qual é a energia de ligação dos elétrons a um material do qual 4,00-eV elétrons são ejetados pela radiação EM de 400 nm? (b) O que há de irrazoável neste resultado? (c) Que suposições são irrazoáveis ou inconsistentes?
Glossary
efeito fotoelétrico: o fenômeno pelo qual alguns materiais ejetam elétrons quando a luz é emitida sobre eles
fóton: um quantum, ou partícula, de radiação eletromagnética
energia de fóton: a quantidade de energia que um fotão tem; E = hf
energia de ligação: também chamada função de trabalho; a quantidade de energia necessária para ejetar um elétron de um material
Soluções selecionadas para problemas & Exercícios
1. 263 nm
3. 3.69 eV
5. 0.483 eV
7. 2.25 eV
9. (a) 264 nm; (b) Ultravioleta
11. 1,95 × 106 m/s
13. (a) 4,02 × 1015 s; (b) 0,256 mW
15. (a) -1,90 eV; (b) Energia cinética negativa; (c) Que os elétrons seriam batidos livres.
