O diagrama de fases da água
Figure 11.23 “Two Versions of the Phase Diagram of Water” mostra o diagrama de fases da água e ilustra que o ponto triplo de água ocorre a 0.01°C e 0.00604 atm (4.59 mmHg). Muito mais reproduzível que o ponto de fusão do gelo, que depende da quantidade de ar dissolvido e da pressão atmosférica, o ponto triplo (273,16 K) é usado para definir a escala de temperatura absoluta (Kelvin). O ponto triplo também representa a pressão mais baixa na qual uma fase líquida pode existir em equilíbrio com o sólido ou vapor. A pressões inferiores a 0,00604 atm, portanto, o gelo não derrete para um líquido à medida que a temperatura aumenta; o sólido sublima diretamente no vapor de água. A sublimação da água a baixa temperatura e pressão pode ser usada para “liofilizar” alimentos e bebidas. Os alimentos ou bebidas são primeiramente resfriados a temperaturas abaixo de zero e colocados em um recipiente no qual a pressão é mantida abaixo de 0,00604 atm. Depois, conforme a temperatura é aumentada, a água sublima, deixando o alimento desidratado (como o usado por mochileiros ou astronautas) ou a bebida em pó (como no café liofilizado).
O diagrama de fases da água ilustrado na parte (b) da Figura 11.23 “Duas Versões do Diagrama de Fases da Água” mostra a fronteira entre gelo e água em uma escala expandida. A curva de fusão do gelo inclina-se para cima e ligeiramente para a esquerda em vez de para cima e para a direita como na Figura 11.22 “Um Diagrama de Fase Típico para uma Substância que Apresenta Três Fases – Sólida, Líquida e Gás – e uma Região Supercrítica”; isto é, o ponto de fusão do gelo diminui com o aumento da pressão; a 100 MPa (987 atm), o gelo derrete a -9°C. A água comporta-se desta forma porque é uma das poucas substâncias conhecidas para a qual o sólido cristalino é menos denso que o líquido (outras incluem o antimónio e o bismuto). Aumentar a pressão do gelo que está em equilíbrio com a água a 0°C e 1 atm tende a aproximar algumas das moléculas, diminuindo assim o volume da amostra. A diminuição no volume (e correspondente aumento na densidade) é menor para um sólido ou líquido do que para um gás, mas é suficiente para derreter parte do gelo.
Figure 11.23 Duas Versões do Diagrama de Fase da Água
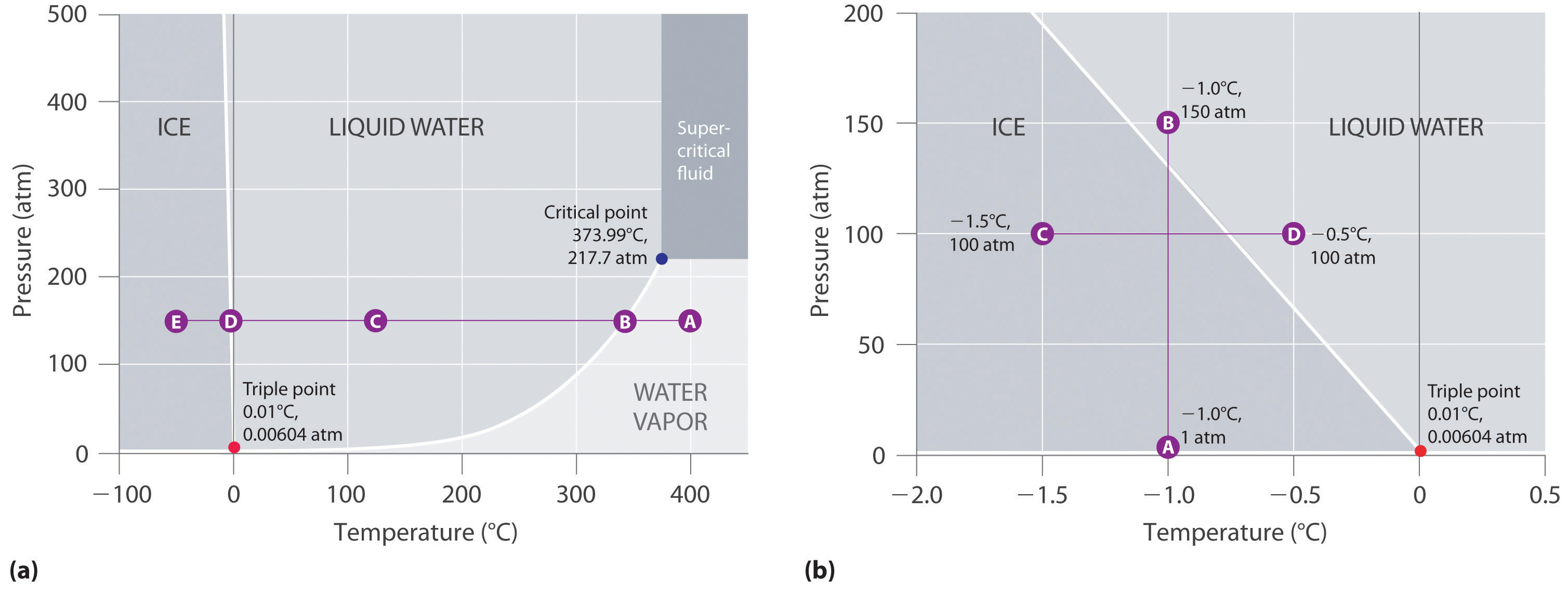
(a) Neste gráfico com eixos lineares de temperatura e pressão, a fronteira entre gelo e água líquida é quase vertical. (b) Este gráfico com uma escala expandida ilustra a diminuição do ponto de fusão com o aumento da pressão. (As letras referem-se aos pontos discutidos no Exemplo 10.)
Na parte (b) da Figura 11.23 “Duas Versões do Diagrama de Fase da Água”, o ponto A está localizado em P = 1 atm e T = -1.0°C, dentro da região sólida (gelo) do diagrama de fase. Como a pressão aumenta para 150 atm enquanto a temperatura permanece a mesma, a linha do ponto A atravessa o limite gelo/água até o ponto B, que fica na região de água líquida. Consequentemente, a aplicação de uma pressão de 150 atm derreterá o gelo a -1,0°C. Já indicamos que a dependência da pressão do ponto de fusão da água é de vital importância. Se o limite sólido/líquido no diagrama de fases da água fosse inclinado para cima e para a direita em vez de para a esquerda, o gelo seria mais denso que a água, os cubos de gelo afundariam, os tubos de água não estourariam quando congelassem e o anticongelante seria desnecessário nos motores de automóveis.
Até recentemente, muitos livros de texto descreviam a patinagem no gelo como sendo possível porque a pressão gerada pela lâmina da patinadora é suficientemente alta para derreter o gelo sob a lâmina, criando assim uma camada lubrificante de água líquida que permite que a lâmina deslize sobre o gelo. Embora esta explicação seja intuitivamente satisfatória, é incorrecta, como podemos demonstrar através de um simples cálculo. Recordando do Capítulo 10 “Gases” que a pressão (P) é a força (F) aplicada por unidade de área (A):
Equação 11.4
P = F A
Para calcular a pressão que um patinador de gelo exerce sobre o gelo, precisamos calcular apenas a força exercida e a área da lâmina de skate. Se assumirmos uma patinadora de 75,0 kg (165 lb), então a força exercida pela patinadora sobre o gelo devido à gravidade é
Equação 11,5
F = mg
onde m é a massa e g é a aceleração devido à gravidade da Terra (9,81 m/s2). Assim a força é
Equação 11,6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Se assumirmos que as lâminas do skate são 2.0 mm de largura e 25 cm de comprimento, então a área do fundo de cada lâmina é
Equação 11,7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Se o patinador desliza sobre um pé, a pressão exercida sobre o gelo é
Equação 11,8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
A pressão é muito inferior à pressão necessária para diminuir o ponto de fusão do gelo em até 1°C, e a experiência indica que é possível patinar mesmo quando a temperatura está bem abaixo de zero. Assim, o derretimento do gelo induzido pela pressão não pode explicar o baixo atrito que permite que patinadores (e pucks de hóquei) deslizem. Pesquisas recentes indicam que a superfície de gelo, onde a matriz ordenada de moléculas de água encontra o ar, consiste em uma ou mais camadas de água quase líquida. Estas camadas, juntamente com o derretimento induzido pelo atrito à medida que uma patinadora avança, parecem explicar tanto a facilidade com que uma patinadora desliza como o facto de a patinagem se tornar mais difícil abaixo dos -7°C, quando o número de camadas de água superficial lubrificante diminui.
