Constante Versnelling
Analyseren van een tweedimensionale projectielbeweging wordt gedaan door het op te splitsen in twee bewegingen: langs de horizontale en de verticale as.
Leerdoelen
Analyseer een tweedimensionale projectielbeweging langs horizontale en verticale assen
Key Takeaways
Key Points
- Constante versnelling in beweging in twee dimensies volgt over het algemeen een projectielpatroon.
- Projectielbeweging is de beweging van een voorwerp dat in de lucht wordt geworpen of geprojecteerd, onderhevig aan alleen de (verticale) versnelling ten gevolge van de zwaartekracht.
- We analyseren tweedimensionale projectielbeweging door deze op te splitsen in twee onafhankelijke eendimensionale bewegingen langs de verticale en de horizontale as.
Key Terms
- kinematisch: van of betrekking hebbend op beweging of kinematica
Projectielbeweging is de beweging van een voorwerp dat in de lucht wordt geworpen, of geprojecteerd, en dat alleen onderworpen is aan de zwaartekracht. Het voorwerp wordt een projectiel genoemd, en zijn baan wordt zijn baan genoemd. De beweging van vallende voorwerpen is een eenvoudige eendimensionale vorm van projectielbeweging waarbij geen horizontale beweging plaatsvindt. Bij een tweedimensionale projectielbeweging, zoals die van een voetbal of een ander gegooid voorwerp, is er zowel een verticale als een horizontale component in de beweging.
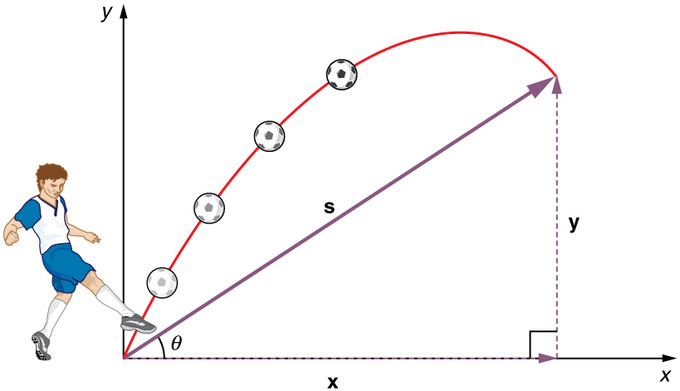
Projectielbeweging: Het gooien van een steen of het schoppen van een bal levert over het algemeen een projectiel bewegingspatroon op dat zowel een verticale als een horizontale component heeft.
Het belangrijkste feit om te onthouden is dat bewegingen langs loodrechte assen onafhankelijk zijn en dus afzonderlijk kunnen worden geanalyseerd. De sleutel tot het analyseren van een tweedimensionale projectielbeweging is deze op te splitsen in twee bewegingen, een langs de horizontale as en de andere langs de verticale. Om de beweging te beschrijven moeten we te maken hebben met snelheid en versnelling, en met verplaatsing.
We zullen aannemen dat alle krachten behalve de zwaartekracht (zoals luchtweerstand en wrijving, bijvoorbeeld) te verwaarlozen zijn. De componenten van de versnelling zijn dan heel eenvoudig: \text{a}_\text{y} = – -9,81 \frac{\text{m}}{text{s}^2} (we nemen aan dat de beweging op voldoende kleine hoogte bij het aardoppervlak plaatsvindt, zodat de versnelling door de zwaartekracht constant is). Omdat de versnelling door de zwaartekracht alleen in verticale richting optreedt, is \text{a}_\text{x} = 0. De kinematische vergelijkingen die de beweging in de richting van respectievelijk \text{x} en \text{y} beschrijven, kunnen dus worden gebruikt:
\text{x} = \text{x}_0 + \text{v}_\text{x} \text{t}
\text{v}_\text{y}=\text{v}_{0\text{y}}+\text{a}_\text{y} \text{t}
\text{y}=\text{y}_0+\text{v}_{0\text{y}} \text{t}+\frac{1}{2}\text{a}_\text{y} \text{t}^2
text{v}_\text{y}^2=\text{v}_{0\text{y}}^2+2\text{a}_\text{y}(\text{y}-\text{y}_0)
We analyseren de tweedimensionale projectielbeweging door deze op te splitsen in twee onafhankelijke eendimensionale bewegingen langs de verticale en de horizontale as. De horizontale beweging is eenvoudig, want \text{a}_\text{x} = 0 en \text{v}_\text{x} is dus constant. De snelheid in verticale richting begint af te nemen naarmate een voorwerp stijgt; op zijn hoogste punt is de verticale snelheid nul. Als een voorwerp weer naar de aarde daalt, neemt de verticale snelheid weer in grootte toe, maar wijst in de tegengestelde richting van de aanvankelijke verticale snelheid. De bewegingen van x en y kunnen worden gecombineerd om de totale snelheid op een bepaald punt van de baan te verkrijgen.7081
