Test di Wald: Definizione, esempi, esecuzione del test

Test di ipotesi > Test di Wald

Che cos’è il test di Wald?

Il test di Wald può dirti quali variabili del modello stanno contribuendo in modo significativo.

Il test di Wald (chiamato anche Wald Chi-Squared Test) è un modo per scoprire se le variabili esplicative in un modello sono significative. “Significativo” significa che aggiungono qualcosa al modello; le variabili che non aggiungono nulla possono essere eliminate senza influenzare il modello in alcun modo significativo. Il test può essere usato per una moltitudine di modelli diversi, compresi quelli con variabili binarie o continue.
L’ipotesi nulla per il test è: qualche parametro = qualche valore. Per esempio, potreste studiare se il peso è influenzato dal mangiare cibo spazzatura due volte a settimana. “Peso” sarebbe il vostro parametro. Il valore potrebbe essere zero (indicando che non pensate che il peso sia influenzato dal mangiare cibo spazzatura). Se l’ipotesi nulla è rifiutata, suggerisce che le variabili in questione possono essere rimosse senza troppi danni al modello.

• Se il test di Wald mostra che i parametri per certe variabili esplicative sono zero, si possono rimuovere le variabili dal modello.
• Se il test mostra che i parametri non sono zero, si dovrebbero includere le variabili nel modello.

Il test di Wald è solitamente parlato in termini di chi-quadrato, perché la distribuzione di campionamento (come n si avvicina all’infinito) è solitamente nota. Questa variante del test è a volte chiamata Wald Chi-Squared Test per differenziarlo dal Wald Log-Linear Chi-Square Test, che è una variante non parametrica basata sul log odds ratio.

Confronto con altri test

Il test di Wald è una approssimazione del Likelihood Ratio Test. Tuttavia, è possibile eseguirlo con un solo modello (il test LR ne richiede almeno due). È anche più ampiamente applicabile del LRT: spesso, è possibile eseguire un Wald in situazioni in cui non è possibile eseguire altri test.

Per grandi valori di n, il test di Wald è approssimativamente equivalente al t-test; entrambi i test rifiuteranno gli stessi valori per grandi dimensioni del campione. I test Wald, LRT e del moltiplicatore di Lagrange sono tutti equivalenti quando le dimensioni del campione si avvicinano all’infinito (chiamato “asintoticamente equivalente”). Tuttavia, i campioni di dimensioni finite, specialmente quelli più piccoli, è probabile che diano risultati molto diversi.

Agresti (1990) suggerisce di usare la LRT invece del test di Wald per campioni di piccole dimensioni o se i parametri sono grandi. Una dimensione “piccola” del campione è inferiore a circa 30.

Eseguire il test

Hai bisogno di aiuto per una domanda sui compiti? Controlla la nostra pagina di tutoring!

La formula della statistica del test di Wald è: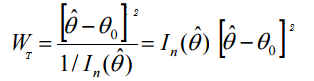

dove:

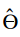• = Estimatore di massima verosimiglianza (MLE),
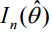• = informazione attesa di Fisher (valutata al MLE).

In pratica, il test cerca differenze: Θ0 – Θ. I passi generali sono:

1. Trova il MLE.
2. Trova l’informazione attesa di Fisher.
3. Valuta l’informazione di Fisher al MLE.

Con la combinazione del MLE e dell’informazione di Fisher, il test di Wald è molto complesso da lavorare e non è solitamente calcolato a mano. Molte applicazioni software possono eseguire il test.

• Stata: usare il comando test.
• R: vedere le istruzioni del test WALD per R (scarica un PDF) dall’Università di Toronto.
• SAS: usare la dichiarazione TEST. WALD è il default se non viene specificato alcun test.

Riferimento:
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.

——————————————————————————

Hai bisogno di aiuto per un compito a casa o per un test? Con Chegg Study, puoi ottenere soluzioni passo dopo passo alle tue domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!