
Pitagora di Samo (570-495 BCE)
Biografia – Chi era Pitagora
A volte si sostiene che dobbiamo la matematica pura a Pitagora, ed è spesso chiamato il primo “vero” matematico. Ma, sebbene il suo contributo sia stato chiaramente importante, egli rimane comunque una figura controversa.
Egli stesso non ha lasciato scritti matematici, e molto di ciò che sappiamo sul pensiero pitagorico ci viene dagli scritti di Filolao e di altri studiosi pitagorici successivi. Infatti, non è affatto chiaro se molti (o addirittura nessuno) dei teoremi a lui attribuiti siano stati effettivamente risolti da Pitagora personalmente o dai suoi seguaci.
La scuola da lui fondata a Crotone nell’Italia meridionale intorno al 530 a.C. fu il nucleo di una setta pitagorica piuttosto bizzarra. Sebbene il pensiero pitagorico fosse largamente dominato dalla matematica, era anche profondamente mistico, e Pitagora impose le sue filosofie quasi religiose, il rigido vegetarismo, la vita in comune, i riti segreti e le strane regole a tutti i membri della sua scuola (inclusi editti bizzarri e apparentemente casuali sul non urinare mai verso il sole, non sposare mai una donna che indossa gioielli d’oro, non passare mai un asino steso per strada, non mangiare o anche solo toccare le fave nere, ecc) .
I membri erano divisi in “mathematikoi” (o “apprendisti”), che estendevano e sviluppavano il lavoro più matematico e scientifico che Pitagora stesso aveva iniziato, e gli “akousmatikoi” (o “ascoltatori”), che si concentravano sugli aspetti più religiosi e ritualistici dei suoi insegnamenti. Ci fu sempre una certa quantità di attrito tra i due gruppi e alla fine la setta fu coinvolta in alcune feroci lotte locali e alla fine si disperse. Il risentimento si sviluppò contro la segretezza e l’esclusività dei pitagorici e, nel 460 a.C., tutti i loro luoghi di riunione furono bruciati e distrutti, con almeno 50 membri uccisi nella sola Crotone.
Il dettame dominante della scuola di Pitagora era “Tutto è numero” o “Dio è numero”, e i pitagorici praticavano effettivamente una sorta di numerologia o culto dei numeri, e consideravano ogni numero come avente un proprio carattere e significato. Per esempio, il numero uno era il generatore di tutti i numeri; due rappresentava l’opinione; tre, l’armonia; quattro, la giustizia; cinque, il matrimonio; sei, la creazione; sette, i sette pianeti o “stelle erranti”; ecc. I numeri dispari erano considerati come femminili e i numeri pari come maschili.
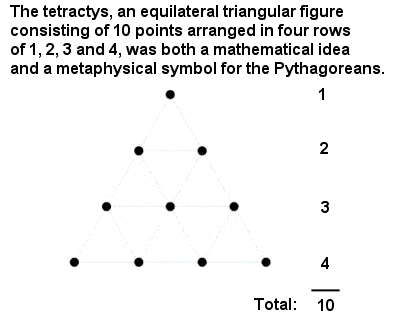
La Tetractys
Il numero più sacro di tutti era “Tetractys” o dieci, un numero triangolare composto dalla somma di uno, due, tre e quattro. È un grande tributo alle conquiste intellettuali dei pitagorici il fatto che essi dedussero il posto speciale del numero 10 da un argomento matematico astratto piuttosto che da qualcosa di banale come contare le dita di due mani.
Tuttavia, Pitagora e la sua scuola – così come una manciata di altri matematici dell’antica Grecia – furono in gran parte responsabili dell’introduzione di una matematica più rigorosa di quella precedente, costruita a partire dai primi principi utilizzando assiomi e logica. Prima di Pitagora, per esempio, la geometria era stata solo un insieme di regole derivate dalla misurazione empirica.
Pitagora scoprì che si poteva costruire un sistema matematico completo, dove gli elementi geometrici corrispondevano a numeri, e dove i numeri interi e i loro rapporti erano tutto ciò che era necessario per stabilire un intero sistema di logica e verità.
Il Teorema di Pitagora
E’ principalmente ricordato per quello che è diventato noto come il Teorema di Pitagora (o il Teorema di Pitagora): che, per qualsiasi triangolo rettangolo, il quadrato della lunghezza dell’ipotenusa (il lato più lungo, opposto all’angolo retto) è uguale alla somma dei quadrati degli altri due lati (o “gambe”).
Scritto come equazione: a2 + b2 = c2.
Quello che Pitagora e i suoi seguaci non hanno capito è che questo funziona anche per qualsiasi forma: così, l’area di un pentagono sull’ipotenusa è uguale alla somma dei pentagoni sugli altri due lati, come per un semicerchio o qualsiasi altra forma regolare (o anche irregolare).
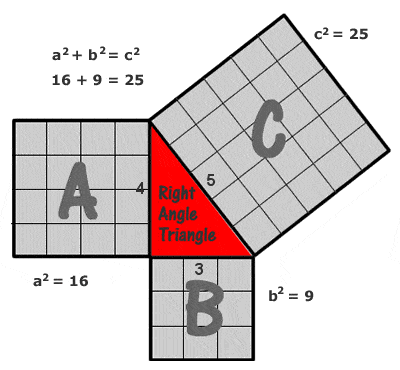
Teorema di Pitagora (Pitagora)
L’esempio più semplice e più comunemente citato di un triangolo pitagorico è quello con lati di 3, 4 e 5 unità (32 + 42 = 52, come si può vedere disegnando una griglia di quadrati unitari su ogni lato come nel diagramma a destra), ma ci sono un numero potenzialmente infinito di altri “triangoli pitagorici” interi, a partire da (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), ecc. Va notato, tuttavia, che (6, 8, 10) non è quello che è noto come un triplo pitagorico “primitivo”, perché è solo un multiplo di (3, 4, 5).
Il Teorema di Pitagora e le proprietà dei triangoli rettangoli sembrano essere lo sviluppo matematico più antico e diffuso dopo l’aritmetica e la geometria di base, ed è stato toccato in alcuni dei più antichi testi matematici di Babilonia ed Egitto, risalenti a oltre mille anni prima. Una delle prove più semplici proviene dall’antica Cina, e probabilmente risale a ben prima della nascita di Pitagora. Fu Pitagora, però, a dare al teorema la sua forma definitiva, anche se non è chiaro se Pitagora stesso l’abbia definitivamente dimostrato o semplicemente descritto. In ogni caso, è diventato uno dei teoremi matematici più conosciuti, e oggi esistono ben 400 prove diverse, alcune geometriche, altre algebriche, altre che coinvolgono equazioni differenziali avanzate, ecc.
Presto divenne evidente, però, che erano possibili anche soluzioni non intere, così che un triangolo isoscele con i lati 1, 1 e √2, per esempio, ha anche un angolo retto, come i Babilonesi avevano scoperto secoli prima. Tuttavia, quando l’allievo di Pitagora, Ippaso, cercò di calcolare il valore di √2, trovò che non era possibile esprimerlo come frazione, indicando così la potenziale esistenza di un intero nuovo mondo di numeri, i numeri irrazionali (numeri che non possono essere espressi come semplici frazioni di interi). Questa scoperta mandò in frantumi l’elegante mondo matematico costruito da Pitagora e dai suoi seguaci, e l’esistenza di un numero che non poteva essere espresso come il rapporto di due creazioni di Dio (che è il modo in cui pensavano ai numeri interi) mise in pericolo l’intero sistema di credenze del culto.
Il povero Ippaso fu apparentemente affogato dai Pitagorici in segreto per aver trasmesso questa importante scoperta al mondo esterno. Ma la sostituzione dell’idea della divinità dei numeri interi con il concetto più ricco del continuo, fu uno sviluppo essenziale nella matematica. Segnò la vera nascita della geometria greca, che si occupa di linee e piani e angoli, che sono tutti continui e non discreti.
Tra le altre sue conquiste in geometria, Pitagora (o almeno i suoi seguaci, i pitagorici) capì anche che la somma degli angoli di un triangolo è uguale a due angoli retti (180°), e probabilmente anche la generalizzazione che afferma che la somma degli angoli interni di un poligono con n lati è uguale a (2n – 4) angoli retti, e che la somma dei suoi angoli esterni è uguale a 4 angoli retti. Erano in grado di costruire figure di una data area, e di usare semplice algebra geometrica, per esempio per risolvere equazioni come a(a – x) = x2 con mezzi geometrici.
I Pitagorici stabilirono anche le basi della teoria dei numeri, con le loro indagini sui numeri triangolari, quadrati e anche perfetti (numeri che sono la somma dei loro divisori). Scoprirono diverse nuove proprietà dei numeri quadrati, come ad esempio che il quadrato di un numero n è uguale alla somma dei primi n numeri dispari (ad esempio 42 = 16 = 1 + 3 + 5 + 7). Hanno anche scoperto almeno la prima coppia di numeri amicabili, 220 e 284 (i numeri amicabili sono coppie di numeri per i quali la somma dei divisori di un numero è uguale all’altro numero, ad esempio i divisori propri di 220 sono 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, la cui somma è 284; e i divisori propri di 284 sono 1, 2, 4, 71 e 142, la cui somma è 220).
Teoria della musica
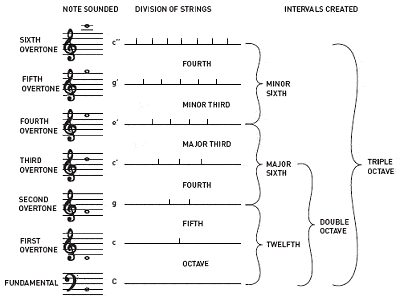
A Pitagora si attribuisce la scoperta dei rapporti tra toni musicali armoniosi
A Pitagora si attribuisce anche la scoperta che gli intervalli tra note musicali armoniose hanno sempre rapporti di numeri interi. Per esempio, suonando mezza lunghezza di una corda di chitarra si ottiene la stessa nota della corda aperta, ma un’ottava più alta; un terzo di lunghezza dà una nota diversa ma armoniosa; ecc.
I rapporti di numeri non interi, invece, tendono a dare suoni dissonanti. In questo modo, Pitagora ha descritto i primi quattro sovratoni che creano gli intervalli comuni che sono diventati i mattoni primari dell’armonia musicale: l’ottava (1:1), la quinta perfetta (3:2), la quarta perfetta (4:3) e la terza maggiore (5:4). Il modo più antico di accordare la scala cromatica di 12 note è noto come accordatura pitagorica, ed è basato su una pila di quinte perfette, ciascuna accordata nel rapporto 3:2.
Il mistico Pitagora fu così eccitato da questa scoperta che si convinse che l’intero universo era basato sui numeri, e che i pianeti e le stelle si muovevano secondo equazioni matematiche, che corrispondevano a note musicali, e così produsse una sorta di sinfonia, la “Musical Universalis” o “Musica delle sfere”.
| << Indietro alla matematica greca | Avanti a Platone >> |
