MATH 1314: College Algebra

Sappiamo come trovare la radice quadrata di qualsiasi numero reale positivo. In modo simile, possiamo trovare la radice quadrata di un numero negativo. La differenza è che la radice non è reale. Se il valore del radicando è negativo, si dice che la radice è un numero immaginario. Il numero immaginario i è definito come la radice quadrata di 1 negativo.

Quindi, usando le proprietà dei radicali,

Si può scrivere la radice quadrata di qualsiasi numero negativo come multiplo di i. Consideriamo la radice quadrata di -25.

Usiamo 5i e non -testo{5}i\ perché la radice principale di 25 è quella positiva.

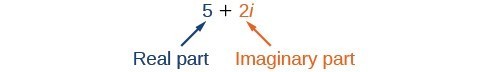
Figura 1

Un numero complesso è la somma di un numero reale e un numero immaginario. Un numero complesso è espresso in forma standard quando si scrive a + bi dove a è la parte reale e bi è la parte immaginaria. Per esempio, 5+2i\ è un numero complesso. Così, anche, è 3+4\sqrt{3}i\.

I numeri immaginari si distinguono dai numeri reali perché un numero immaginario al quadrato produce un numero reale negativo. Ricordiamo che quando un numero reale positivo viene elevato al quadrato, il risultato è un numero reale positivo e quando un numero reale negativo viene elevato al quadrato, di nuovo, il risultato è un numero reale positivo. I numeri complessi sono una combinazione di numeri reali e immaginari.