In questa sezione, familiarizzeremo con le operazioni e le notazioni degli insiemi, in modo da poter applicare questi concetti ai problemi di conteggio e di probabilità. Iniziamo definendo alcuni termini.
Un insieme è una collezione di oggetti, e i suoi membri sono chiamati elementi dell’insieme. Nominiamo l’insieme usando lettere maiuscole e racchiudiamo i suoi membri tra parentesi graffe. Supponiamo di dover elencare i membri del club degli scacchi. Usiamo la seguente notazione dell’insieme.
C ={Ken, Bob, Tran, Shanti, Eric}
Un insieme che non ha membri è chiamato insieme vuoto. L’insieme vuoto è indicato con il simbolo Ø.
Due insiemi sono uguali se hanno gli stessi elementi.
Un insieme A è un sottoinsieme di un insieme B se ogni membro di A è anche un membro di B.
Supponiamo C = {Al, Bob, Chris, David, Ed} e A = {Bob, David}. Allora A è un sottoinsieme di C, scritto come 
.
Ogni insieme è un sottoinsieme di se stesso, e l’insieme vuoto è un sottoinsieme di ogni insieme.
Unione di due insiemi
Sia A e B due insiemi, allora l’unione di A e B, scritta come 
, è l’insieme di tutti gli elementi che sono o in A o in B, o in entrambi A e B.
Intersezione di due insiemi
Siano A e B due insiemi, allora l’intersezione di A e B, scritta come 
, è l’insieme di tutti gli elementi che sono comuni ai due insiemi A e B.
Un insieme universale U è l’insieme costituito da tutti gli elementi considerati.
Complemento di un insieme
Sia A un qualsiasi insieme, allora il complemento dell’insieme A, scritto come 
, è l’insieme costituito dagli elementi dell’insieme universale U che non sono in A.
Insiemi disgiunti
Due insiemi A e B si dicono insiemi disgiunti se la loro intersezione è un insieme vuoto.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {arancio, verde, indaco, viola}Per capire meglio, supponiamo che l’insieme universale U rappresenti i colori dello spettro, e P i colori primari, allora rappresenta quei colori dello spettro che non sono colori primari.
.
= {rosso, giallo, blu, verde}
= {arancio, indaco, viola}
= {rosso, giallo, blu, viola} = {violetto}Diagrammi di Venn
Ora usiamo i diagrammi di Venn per illustrare le relazioni tra insiemi. Alla fine del 1800, un logico inglese chiamato John Venn sviluppò un metodo per rappresentare le relazioni tra gli insiemi. Egli rappresentò queste relazioni usando diagrammi, che ora sono conosciuti come diagrammi di Venn. Un diagramma di Venn rappresenta un insieme come l’interno di un cerchio. Spesso due o più cerchi sono racchiusi in un rettangolo dove il rettangolo rappresenta l’insieme universale. Visualizzare un’intersezione o un’unione di un insieme è facile. In questa sezione, useremo principalmente i diagrammi di Venn per ordinare varie popolazioni e contare oggetti.
|
(a) |
(b) |
(c) |
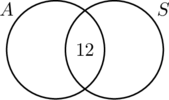
Perché 30 persone hanno guidato auto con cambio automatico, il cerchio A deve contenere 30 elementi. Questo significa che x + 12 = 30, o x = 18. Allo stesso modo, poiché 20 persone hanno guidato auto con trasmissioni standard, il cerchio B deve contenere 20 elementi, o y +12 = 20 che a sua volta fa y = 8.
Ora che tutte le informazioni sono ordinate, è facile leggere dal diagramma che 18 persone hanno guidato solo auto con cambio automatico, 12 persone hanno guidato entrambi i tipi di auto, e 8 hanno guidato solo auto con trasmissioni standard. Pertanto, 18 + 12 + 8 = 38 persone hanno partecipato al sondaggio.
|
(a) |
(b) |
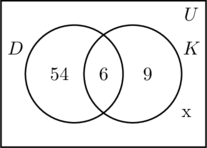
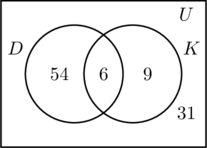
Compiliamo le tre regioni associate agli insiemi D e K nello stesso modo di prima. Poiché 100 persone hanno partecipato al sondaggio, il rettangolo che rappresenta l’insieme universale U deve contenere 100 oggetti. Lasciamo che x rappresenti le persone dell’insieme universale che non sono né nell’insieme D né in K. Ciò significa 54 + 6 + 9 + x = 100, o x = 31.
Ci sono quindi 31 persone nel sondaggio che non hanno visitato nessuno dei due luoghi.
- 50 fanno jogging, 30 nuotano e 35 vanno in bicicletta
- 14 fanno jogging e nuotano
- 7 nuotano e vanno in bicicletta
- 9 fanno jogging e vanno in bicicletta
- 3 persone praticano tutte e tre le attività
Soluzione
|
(a) |
(b) |
(c) |
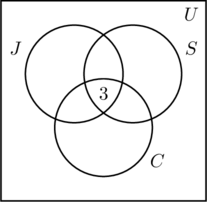
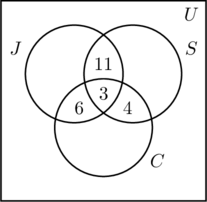
Mettiamo un 3 nella regione più interna della figura (a) perché rappresenta il numero di persone che partecipano a tutte e tre le attività. Poi calcoliamo x, y e z.
- Poiché 14 persone fanno jogging e nuotano, x +3 = 14, o x = 11.
- Il fatto che 9 persone fanno jogging e vanno in bicicletta risulta in y + 3 = 9, o y = 6.
- Siccome 7 persone nuotano e vanno in bicicletta, z + 3 = 7, o z = 4.
- Questa informazione è rappresentata nella figura (b).
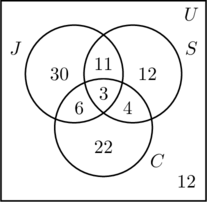
- Siccome 50 persone fanno jogging, m + 11 + 6 + 3 = 50, o m = 30.
- 30 persone nuotano, quindi, n + 11 + 4 + 3 = 30, o n = 12.
- 35 persone vanno in bicicletta, quindi, p + 6 + 4 + 3 = 35, o p = 22.
- Sommando tutte le voci di tutti e tre gli insiemi, otteniamo una somma di 88. Poiché sono state intervistate 100 persone, il numero all’interno dell’insieme universale ma al di fuori di tutti e tre gli insiemi è 100 – 88, o 12.
- Nella figura (c), le informazioni sono ordinate, e le domande possono essere facilmente risposte.
Domande pratiche
1. Sia l’insieme universale U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h}, e W = {a, c, e, g, i}. Elenca i membri dei seguenti insiemi:
a. 
b. 
2. Considerare i seguenti insiemi: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, Influenza, Norovirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella}, e C = {SARS, Listeria, Tubercolosi, H5N1, Salmonella, HIV, COVID-19}. Elenca i membri dei seguenti insiemi:
a. 
b. 
3. Un sondaggio tra gli atleti ha rivelato che per i loro piccoli dolori, 30 usavano l’aspirina, 50 l’ibuprofene e 15 entrambi. Tutti gli atleti intervistati hanno usato almeno uno dei due antidolorifici. Quanti atleti sono stati intervistati?
4. Uno studio su 150 studenti delle scuole superiori ha scoperto che 25 hanno riferito di avere una precedente commozione cerebrale o un trauma cranico, 52 hanno riferito di aver sperimentato una malattia mentale, e 15 hanno riferito entrambi i risultati. Quanti studenti non hanno riportato nessuno dei due risultati?
5. Un sondaggio su 100 studenti della Ryerson University rileva che 50 sono abbonati a Netflix, 40 ad Amazon Prime e 30 a Disney+. Di questi, 15 sono abbonati sia a Netflix che ad Amazon Prime, 10 sia ad Amazon Prime che a Disney+, 10 sia a Netflix che a Disney+, e 5 hanno tutti e tre i servizi di abbonamento. Disegna un diagramma di Venn e determina quanto segue:
a. Il numero di studenti abbonati ad Amazon Prime ma non agli altri due servizi di streaming.
b. Il numero di studenti abbonati a Netflix o Amazon Prime ma non a Disney+.
c. Il numero di studenti non abbonati a nessuno di questi servizi.
c.