Un gruppo 
è un insieme finito o infinito di elementi insieme a un’operazione binaria (chiamata operazione di gruppo) che insieme soddisfano le quattro proprietà fondamentali di chiusura, associatività, proprietà dell’identità e proprietà inversa. L’operazione rispetto alla quale un gruppo è definito è spesso chiamata “operazione di gruppo”, e un insieme si dice essere un gruppo “sotto” questa operazione. Gli elementi 
, 
, 
, … con operazione binaria tra 
e 
denotata 
formano un gruppo se
1. Chiusura: se 
e 
sono due elementi in 
, allora il prodotto 
è anche in 
.
2. Associatività: La moltiplicazione definita è associativa, cioè, per tutti i 
, 
.
3. Identità: C’è un elemento di identità 
(detto anche 1, 
o 
) tale che 
per ogni elemento 
.
4. Inverso: Ci deve essere un inverso (o reciproco) di ogni elemento. Quindi, per ogni elemento 
di 
, l’insieme contiene un elemento 
tale che 
.
Un gruppo è un monoide ognuno dei cui elementi è invertibile.
Un gruppo deve contenere almeno un elemento, con l’unico (fino all’isomorfismo) gruppo a elemento singolo noto come gruppo banale.
Lo studio dei gruppi è noto come teoria dei gruppi. Se ci sono un numero finito di elementi, il gruppo è chiamato gruppo finito e il numero di elementi è chiamato ordine del gruppo. Un sottoinsieme di un gruppo che è chiuso sotto l’operazione di gruppo e l’operazione inversa è chiamato sottogruppo. Anche i sottogruppi sono gruppi, e molti gruppi comunemente incontrati sono in effetti sottogruppi speciali di qualche gruppo più generale più grande.
Un esempio base di un gruppo finito è il gruppo simmetrico 
, che è il gruppo delle permutazioni (o “sotto permutazione”) di 
oggetti. Il gruppo infinito più semplice è l’insieme dei numeri interi sotto addizione abituale. Per i gruppi continui, si possono considerare i numeri reali o l’insieme delle matrici invertibili 
. Questi ultimi due sono esempi di gruppi di Lie.
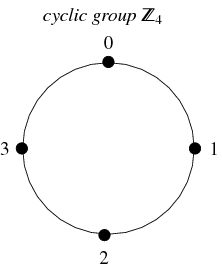
Un tipo di gruppo molto comune sono i gruppi ciclici. Questo gruppo è isomorfo al gruppo dei numeri interi (modulo 
), si chiama 
, 
, o 
, ed è definito per ogni intero 
. È chiuso sotto l’addizione, associativo e ha inversioni uniche. I numeri da 0 a 
rappresentano i suoi elementi, con l’elemento identità rappresentato da 0, e l’inverso di 
è rappresentato da 
.
Una mappa tra due gruppi che conserva l’identità e l’operazione di gruppo è chiamata omomorfismo. Se un omomorfismo ha un inverso che è anche un omomorfismo, allora si chiama isomorfismo e i due gruppi sono detti isomorfi. Due gruppi che sono isomorfi l’uno all’altro sono considerati “uguali” se visti come gruppi astratti. Per esempio, il gruppo delle rotazioni di un quadrato, illustrato sotto, è il gruppo ciclico 
.
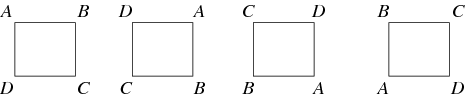
In generale, un’azione di gruppo è quando un gruppo agisce su un insieme, permutando i suoi elementi, in modo che la mappa dal gruppo al gruppo di permutazione dell’insieme sia un omomorfismo. Per esempio, le rotazioni di un quadrato sono un sottogruppo delle permutazioni dei suoi angoli. Un’importante azione di gruppo per qualsiasi gruppo 
è la sua azione su se stesso per coniugazione. Questi sono solo alcuni dei possibili automorfismi di gruppo. Un altro tipo importante di azione di gruppo è una rappresentazione di gruppo, dove il gruppo agisce su uno spazio vettoriale tramite mappe lineari invertibili. Quando il campo dello spazio vettoriale sono i numeri complessi, a volte una rappresentazione è chiamata modulo CG.
Le azioni di gruppo, e in particolare le rappresentazioni, sono molto importanti nelle applicazioni, non solo alla teoria dei gruppi, ma anche alla fisica e alla chimica. Poiché un gruppo può essere pensato come un oggetto matematico astratto, lo stesso gruppo può presentarsi in diversi contesti. È quindi utile pensare a una rappresentazione del gruppo come a una particolare incarnazione del gruppo, che può anche avere altre rappresentazioni. Una rappresentazione irriducibile di un gruppo è una rappresentazione per la quale non esiste una trasformazione unitaria che trasformi la matrice di rappresentazione in forma diagonale a blocchi. Le rappresentazioni irriducibili hanno una serie di proprietà notevoli, come formalizzato nel teorema di ortogonalità di gruppo.