Obiettivi di apprendimento
Alla fine di questa sezione, sarai in grado di:
- Descrivere un tipico esperimento di effetto fotoelettrico.
- Determinare la massima energia cinetica dei fotoelettroni espulsi da fotoni di un’energia o lunghezza d’onda, quando viene data la massima energia cinetica dei fotoelettroni per una diversa energia fotonica o lunghezza d’onda.
Quando la luce colpisce i materiali, può espellere elettroni da essi. Questo è chiamato effetto fotoelettrico, cioè la luce (foto) produce elettricità. Un uso comune dell’effetto fotoelettrico è nei misuratori di luce, come quelli che regolano il diaframma automatico su vari tipi di macchine fotografiche. In modo simile, un altro uso è nelle celle solari, come probabilmente hai nella tua calcolatrice o hai visto su un tetto o un cartello stradale. Queste fanno uso dell’effetto fotoelettrico per convertire la luce in elettricità per far funzionare diversi dispositivi.

Figura 1. L’effetto fotoelettrico può essere osservato facendo cadere la luce sulla piastra metallica in questo tubo sottovuoto. Gli elettroni espulsi dalla luce sono raccolti sul filo del collettore e misurati come corrente. Una tensione di ritardo tra il filo collettore e la piastra può essere regolata in modo da determinare l’energia degli elettroni espulsi. Per esempio, se è sufficientemente negativa, nessun elettrone raggiungerà il filo. (credit: P.P. Urone)
Questo effetto è noto da più di un secolo e può essere studiato utilizzando un dispositivo come quello mostrato nella figura 1. Questa figura mostra un tubo sottovuoto con una piastra metallica e un filo collettore che sono collegati da una fonte di tensione variabile, con il collettore più negativo della piastra. Quando la luce (o altre radiazioni EM) colpisce la piastra nel tubo sottovuoto, può espellere elettroni. Se gli elettroni hanno un’energia in elettronvolt (eV) maggiore della differenza di potenziale tra la piastra e il filo in volt, alcuni elettroni saranno raccolti sul filo. Poiché l’energia degli elettroni in eV è eV, dove q è la carica degli elettroni e V è la differenza di potenziale, l’energia degli elettroni può essere misurata regolando la tensione di ritardo tra il filo e la piastra. La tensione che impedisce agli elettroni di raggiungere il filo è uguale all’energia in eV. Per esempio, se -3,00 V ferma appena gli elettroni, la loro energia è 3,00 eV. Il numero di elettroni espulsi può essere determinato misurando la corrente tra il filo e la piastra. Più luce, più elettroni; un piccolo circuito permette di usare questo dispositivo come un misuratore di luce.
Quello che è veramente importante dell’effetto fotoelettrico è ciò che Albert Einstein ne ha dedotto. Einstein si rese conto che c’erano diverse caratteristiche dell’effetto fotoelettrico che potevano essere spiegate solo se la radiazione EM è essa stessa quantizzata: il flusso apparentemente continuo di energia in un’onda EM è in realtà composto da quanti di energia chiamati fotoni. Nella sua spiegazione dell’effetto fotoelettrico, Einstein definì un’unità quantizzata o quantum di energia EM, che ora chiamiamo fotone, con un’energia proporzionale alla frequenza della radiazione EM. In forma di equazione, l’energia del fotone è E = hf, dove E è l’energia di un fotone di frequenza f e h è la costante di Planck. Questa idea rivoluzionaria sembra simile alla quantizzazione di Planck degli stati energetici negli oscillatori a corpo nero, ma è molto diversa. È la quantizzazione della radiazione EM stessa. Le onde EM sono composte da fotoni e non sono onde continue e lisce come descritto nei precedenti capitoli sull’ottica. La loro energia viene assorbita ed emessa a blocchi, non in modo continuo. Questo è esattamente coerente con la quantizzazione di Planck dei livelli di energia negli oscillatori di corpo nero, poiché questi oscillatori aumentano e diminuiscono la loro energia in passi di hf assorbendo ed emettendo fotoni aventi E = hf. Noi non osserviamo questo con i nostri occhi, perché ci sono così tanti fotoni nelle comuni fonti di luce che i singoli fotoni passano inosservati. (Vedi Figura 2.) La prossima sezione del testo (Photon Energies and the Electromagnetic Spectrum) è dedicata ad una discussione sui fotoni e su alcune delle loro caratteristiche e implicazioni. Per ora, useremo il concetto di fotone per spiegare l’effetto fotoelettrico, proprio come fece Einstein.
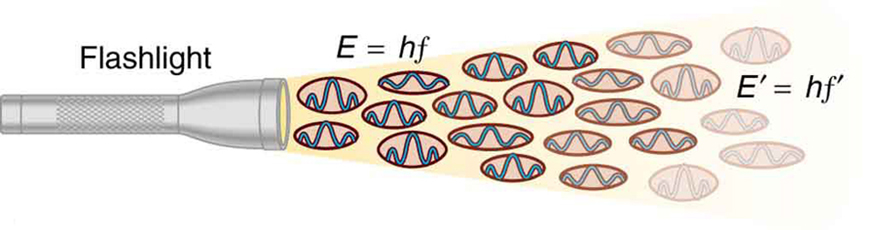
Figura 2. Un’onda EM di frequenza f è composta da fotoni, o singoli quanti di radiazione EM. L’energia di ogni fotone è E = hf, dove h è la costante di Planck e f è la frequenza della radiazione EM. Una maggiore intensità significa più fotoni per unità di superficie. La torcia emette un gran numero di fotoni di molte frequenze diverse, quindi altri hanno energia E′ = hf′, e così via.
L’effetto fotoelettrico ha le proprietà discusse sotto. Tutte queste proprietà sono coerenti con l’idea che i singoli fotoni della radiazione EM sono assorbiti da singoli elettroni in un materiale, con l’elettrone che guadagna l’energia del fotone. Alcune di queste proprietà non sono coerenti con l’idea che la radiazione EM sia una semplice onda. Per semplicità, consideriamo cosa succede con la radiazione EM monocromatica in cui tutti i fotoni hanno la stessa energia hf.
- Se variamo la frequenza della radiazione EM che cade su un materiale, troviamo quanto segue: Per un dato materiale, c’è una frequenza di soglia f0 per la radiazione EM sotto la quale non vengono espulsi elettroni, indipendentemente dall’intensità. I singoli fotoni interagiscono con i singoli elettroni. Così, se l’energia del fotone è troppo piccola per rompere un elettrone, nessun elettrone sarà espulso. Se la radiazione EM fosse una semplice onda, si potrebbe ottenere sufficiente energia aumentando l’intensità.
- Una volta che la radiazione EM cade su un materiale, gli elettroni vengono espulsi senza ritardo. Non appena un singolo fotone di una frequenza sufficientemente alta viene assorbito da un singolo elettrone, l’elettrone viene espulso. Se la radiazione EM fosse una semplice onda, sarebbero necessari diversi minuti per depositare sulla superficie metallica l’energia sufficiente ad espellere un elettrone.
- Il numero di elettroni espulsi per unità di tempo è proporzionale all’intensità della radiazione EM e a nessun’altra caratteristica. La radiazione EM ad alta intensità consiste in un gran numero di fotoni per unità di superficie, con tutti i fotoni che hanno la stessa energia caratteristica hf.
- Se si varia l’intensità della radiazione EM e si misura l’energia degli elettroni espulsi, si trova quanto segue: L’energia cinetica massima degli elettroni espulsi è indipendente dall’intensità della radiazione EM. Poiché ci sono così tanti elettroni in un materiale, è estremamente improbabile che due fotoni interagiscano con lo stesso elettrone allo stesso tempo, aumentando così l’energia data. Invece (come notato in 3 sopra), l’aumento dell’intensità ha come risultato l’espulsione di più elettroni della stessa energia. Se la radiazione EM fosse una semplice onda, una maggiore intensità potrebbe dare più energia, e gli elettroni di maggiore energia sarebbero espulsi.
- L’energia cinetica di un elettrone espulso è uguale all’energia del fotone meno l’energia di legame dell’elettrone nel materiale specifico. Un singolo fotone può dare tutta la sua energia ad un elettrone. L’energia del fotone viene in parte utilizzata per staccare l’elettrone dal materiale. Il resto va nell’energia cinetica dell’elettrone espulso. In forma di equazione, questo è dato da KEe = hf – BE, dove KEe è l’energia cinetica massima dell’elettrone espulso, hf è l’energia del fotone e BE è l’energia di legame dell’elettrone al particolare materiale. (Questa equazione, dovuta a Einstein nel 1905, spiega quantitativamente le proprietà dell’effetto fotoelettrico. Un singolo fotone di radiazione EM (non viene in nessun altro modo) interagisce con un singolo elettrone, fornendo abbastanza energia, BE, per spezzarlo, mentre il resto va in energia cinetica. L’energia di legame è BE = hf0, dove f0 è la frequenza di soglia per il particolare materiale. La figura 3 mostra un grafico di KEe massimo rispetto alla frequenza della radiazione EM incidente che cade su un particolare materiale.
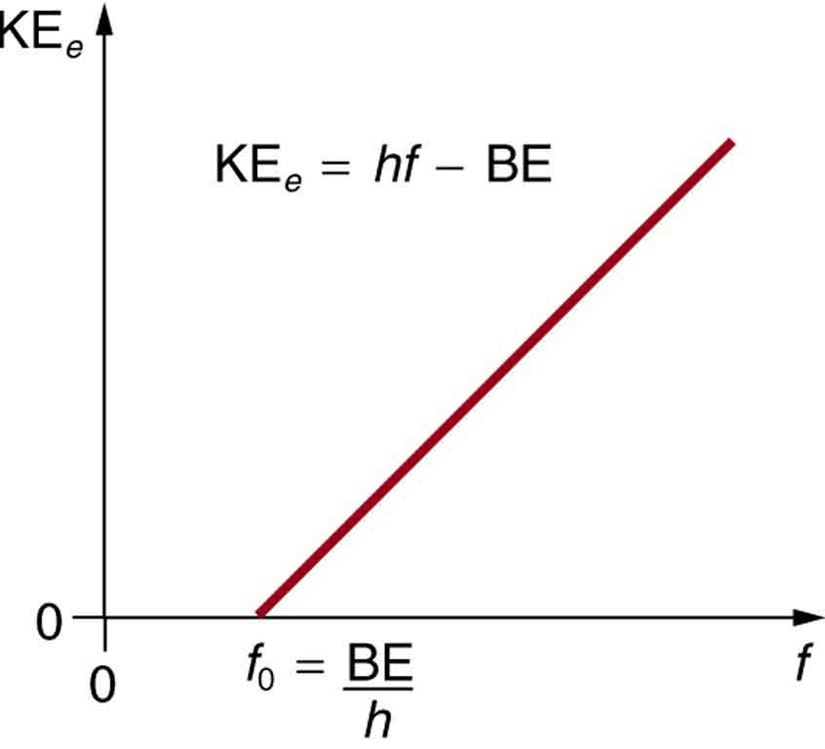
Figura 3. Effetto fotoelettrico. Un grafico dell’energia cinetica di un elettrone espulso, KEe, contro la frequenza della radiazione EM che colpisce un certo materiale. C’è una frequenza di soglia al di sotto della quale nessun elettrone viene espulso, perché il singolo fotone che interagisce con un singolo elettrone non ha energia sufficiente per staccarlo. Sopra l’energia di soglia, KEe aumenta linearmente con f, coerentemente con KEe = hf – BE. La pendenza di questa linea è h – i dati possono essere usati per determinare sperimentalmente la costante di Planck. Einstein diede la prima spiegazione di successo di tali dati proponendo l’idea dei fotoni-quanti di radiazione EM.
L’idea di Einstein che la radiazione EM sia quantizzata fu cruciale per gli inizi della meccanica quantistica. È un concetto molto più generale di quanto la sua spiegazione dell’effetto fotoelettrico possa implicare. Tutta la radiazione EM può anche essere modellata sotto forma di fotoni, e le caratteristiche della radiazione EM sono interamente coerenti con questo fatto. (Come vedremo nella prossima sezione, molti aspetti della radiazione EM, come i pericoli della radiazione ultravioletta (UV), possono essere spiegati solo dalle proprietà dei fotoni). Più famoso per la relatività moderna, Einstein piantò un seme importante per la meccanica quantistica nel 1905, lo stesso anno in cui pubblicò il suo primo articolo sulla relatività speciale. La sua spiegazione dell’effetto fotoelettrico fu la base del premio Nobel assegnatogli nel 1921. Sebbene i suoi altri contributi alla fisica teorica siano stati notati in quel premio, la relatività speciale e generale non sono state pienamente riconosciute, nonostante siano state parzialmente verificate dall’esperimento nel 1921. Sebbene venerato come un eroe, questo grande uomo non ricevette mai il riconoscimento del Nobel per la sua opera più famosa, la relatività. Calcolo dell’energia dei fotoni e dell’effetto fotoelettrico: Una luce viola
1. Qual è l’energia in joule ed elettronvolt di un fotone di luce viola da 420-nm?
2. Qual è l’energia cinetica massima degli elettroni espulsi dal calcio dalla luce viola da 420-nm, dato che l’energia di legame (o funzione di lavoro) degli elettroni per il calcio metallico è 2,71 eV?
Strategia
Per risolvere la parte 1, si noti che l’energia di un fotone è data da E = hf. Per la Parte 2, una volta calcolata l’energia del fotone, è una semplice applicazione di KEe = hf – BE per trovare l’energia cinetica massima dell’elettrone espulso, poiché BE è data.
Soluzione per la Parte 1
L’energia del fotone è data da E = hf.
Siccome ci viene data la lunghezza d’onda piuttosto che la frequenza, risolviamo la nota relazione c = fλ per la frequenza, ottenendo f=frac{c}{lambda}\frac.
Combinando queste due equazioni si ottiene l’utile relazione E=frac{hc}{lambda}.
Ora sostituendo i valori noti si ottiene
displaystyle{E}=frac(6.63 volte10^{-34} di J}cdot{text{ s}) a sinistra(3.00 ^times10^{8}{m/s}}destra)}{ 420 ^times10^{-9}{m}}=4,74 ^times10^{-19}{ J}{4478>
Convertendo in eV, l’energia del fotone è
{displaystyle{E}={4.47 volte10^{-19} J} a destra)\frac{ 1 eV}}{1.6 volte10^{-19}{ J}}=2.96{ eV}
Soluzione per la Parte 2
Trovare l’energia cinetica dell’elettrone espulso è ora una semplice applicazione dell’equazione KEe = hf – BE. Sostituendo l’energia del fotone e l’energia di legame si ottiene KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV.
Discussione
L’energia di questo fotone di 420-nm di luce viola è una piccola frazione di un joule, e quindi non c’è da meravigliarsi che un singolo fotone sia difficile da percepire direttamente – gli esseri umani sono più in sintonia con energie dell’ordine del joule. Ma guardando l’energia in elettronvolt, possiamo vedere che questo fotone ha abbastanza energia per influenzare atomi e molecole. Una molecola di DNA può essere rotta con circa 1 eV di energia, per esempio, e le energie atomiche e molecolari tipiche sono dell’ordine di eV, quindi il fotone UV in questo esempio potrebbe avere effetti biologici. L’elettrone espulso (chiamato fotoelettrone) ha un’energia piuttosto bassa, e non viaggerebbe lontano, se non nel vuoto. L’elettrone verrebbe fermato da un potenziale ritardante di soli 0,26 eV. Infatti, se la lunghezza d’onda del fotone fosse più lunga e la sua energia inferiore a 2,71 eV, allora la formula darebbe un’energia cinetica negativa, un’impossibilità. Questo significa semplicemente che i fotoni di 420-nm con la loro energia di 2,96 eV non sono molto al di sopra della soglia di frequenza. Potete dimostrare da soli che la lunghezza d’onda di soglia è 459 nm (luce blu). Questo significa che se il calcio metallico viene usato in un misuratore di luce, il misuratore sarà insensibile a lunghezze d’onda più lunghe di quelle della luce blu. Un tale misuratore di luce sarebbe completamente insensibile alla luce rossa, per esempio.
PhET Explorations: Effetto Fotoelettrico
Vedi come la luce fa cadere gli elettroni da un bersaglio metallico, e ricrea l’esperimento che ha dato origine al campo della meccanica quantistica.

Clicca per scaricare la simulazione. Esegui usando Java.
Sommario della sezione
- L’effetto fotoelettrico è il processo in cui la radiazione EM espelle gli elettroni da un materiale.
- Einstein propose i fotoni come quanti di radiazione EM aventi energia E = hf, dove f è la frequenza della radiazione.
- Tutta la radiazione EM è composta da fotoni. Come spiegò Einstein, tutte le caratteristiche dell’effetto fotoelettrico sono dovute all’interazione dei singoli fotoni con i singoli elettroni.
- L’energia cinetica massima KEe degli elettroni espulsi (fotoelettroni) è data da KEe = hf – BE, dove hf è l’energia del fotone e BE è l’energia di legame (o funzione lavoro) dell’elettrone al particolare materiale.
Domande concettuali
- La luce visibile è l’unico tipo di radiazione EM che può causare l’effetto fotoelettrico? Quali possono essere spiegati senza fotoni? Questi ultimi sono incompatibili con l’esistenza dei fotoni?
- L’effetto fotoelettrico è una conseguenza diretta del carattere ondulatorio della radiazione EM o del carattere particellare della radiazione EM? Spiega brevemente.
- Gli isolanti (non metalli) hanno un BE più alto dei metalli, ed è più difficile per i fotoni espellere elettroni dagli isolanti. Discutete come questo sia collegato alle cariche libere nei metalli che li rendono buoni conduttori.
- Se prendete e scuotete un pezzo di metallo che ha elettroni al suo interno liberi di muoversi come una corrente, nessun elettrone cade fuori. Eppure, se si riscalda il metallo, gli elettroni possono essere bolliti via. Spiega entrambi questi fatti come si riferiscono alla quantità e alla distribuzione di energia coinvolta nell’agitare l’oggetto rispetto al riscaldarlo.
Problemi & Esercizi
- Qual è la radiazione EM di lunghezza d’onda più lunga che può espellere un fotoelettrone dall’argento, dato che l’energia di legame è 4,73 eV? È nella gamma visibile?
- Trova il fotone di lunghezza d’onda più lunga che può espellere un elettrone dal potassio, dato che l’energia di legame è 2,24 eV. Si tratta di radiazione EM visibile?
- Qual è l’energia di legame in eV degli elettroni nel magnesio, se il fotone di lunghezza d’onda più lunga che può espellere gli elettroni è 337 nm?
- Calcolate l’energia di legame in eV degli elettroni nell’alluminio, se il fotone di lunghezza d’onda più lunga che può espellerli è 304 nm.
- Qual è la massima energia cinetica in eV degli elettroni espulsi dal sodio metallico dalla radiazione EM di 450 nm, dato che l’energia di legame è 2,28 eV?
- La radiazione UV con lunghezza d’onda di 120 nm cade sul metallo oro, al quale gli elettroni sono legati da 4,82 eV. Qual è l’energia cinetica massima dei fotoelettroni espulsi?
- La luce viola di lunghezza d’onda 400 nm espelle elettroni con un’energia cinetica massima di 0,860 eV dal metallo sodio. Qual è l’energia di legame degli elettroni al sodio metallico?
- La radiazione UV di lunghezza d’onda 300 nm cade sul metallo uranio, espellendo elettroni di 0,500 eV. Qual è l’energia di legame degli elettroni al metallo uranio?
- (a) Qual è la lunghezza d’onda della radiazione EM che espelle elettroni da 2,00 eV dal metallo calcio, dato che l’energia di legame è 2,71 eV? (b) Che tipo di radiazione EM è questa?
- Trova la lunghezza d’onda dei fotoni che espellono elettroni da 0,100 eV dal potassio, dato che l’energia di legame è 2,24 eV. Questi fotoni sono visibili?
- Qual è la velocità massima degli elettroni espulsi da un materiale da fotoni di 80-nm, se sono legati al materiale da 4,73 eV?
- Fotoelettroni da un materiale con un’energia di legame di 2,71 eV sono espulsi da fotoni di 420-nm. Una volta espulsi, quanto tempo impiegano questi elettroni a viaggiare per 2,50 cm fino a un dispositivo di rilevamento?
- Un laser con una potenza di 2,00 mW a una lunghezza d’onda di 400 nm viene proiettato sul calcio metallico. (a) Quanti elettroni al secondo vengono espulsi? (b) Quale potenza viene portata via dagli elettroni, dato che l’energia di legame è 2.71 eV?
- (a) Calcolare il numero di fotoelettroni al secondo espulsi da un’area di 1.00-mm 2 di sodio metallico dalla radiazione EM di 500-nm con un’intensità di 1.30 kW/m2 (l’intensità della luce solare sopra l’atmosfera terrestre). (b) Dato che l’energia di legame è 2,28 eV, quale potenza viene portata via dagli elettroni? (c) Gli elettroni portano via meno potenza di quella portata dai fotoni. Dove va a finire l’altra potenza? Come può essere recuperata?
- Risultati irragionevoli. Una luce rossa con una lunghezza d’onda di 700 nm viene proiettata sul metallo magnesio a cui sono legati elettroni per 3,68 eV. (a) Usate KEe = hf – BE per calcolare l’energia cinetica degli elettroni espulsi. (b) Cosa c’è di irragionevole in questo risultato? (c) Quali ipotesi sono irragionevoli o incoerenti?
- Risultati irragionevoli. (a) Qual è l’energia di legame degli elettroni a un materiale da cui vengono espulsi elettroni da 4.00-eV da una radiazione EM di 400-nm? (b) Cosa c’è di irragionevole in questo risultato? (c) Quali ipotesi sono irragionevoli o incoerenti?
Glossario
effetto fotoelettrico: il fenomeno per cui alcuni materiali espellono elettroni quando la luce viene fatta brillare su di loro
fotone: un quantum, o particella, di radiazione elettromagnetica
energia del fotone: la quantità di energia che ha un fotone; E = hf
energia di legame: chiamata anche funzione di lavoro; la quantità di energia necessaria per espellere un elettrone da un materiale
Soluzioni selezionate ai problemi & Esercizi
1. 263 nm
3. 3.69 eV
5. 0.483 eV
7. 2.25 eV
9. (a) 264 nm; (b) Ultravioletto
11. 1,95 × 106 m/s
13. (a) 4,02 × 1015 s; (b) 0,256 mW
15. (a) -1,90 eV; (b) energia cinetica negativa; (c) che gli elettroni sarebbero stati liberati.
