Il diagramma di fase dell’acqua
La figura 11.23 “Due versioni del diagramma di fase dell’acqua” mostra il diagramma di fase dell’acqua e illustra che il punto triplo dell’acqua avviene a 0,01°C e 0,00604 atm (4,59 mmHg). Molto più riproducibile del punto di fusione del ghiaccio, che dipende dalla quantità di aria dissolta e dalla pressione atmosferica, il punto triplo (273,16 K) è usato per definire la scala di temperatura assoluta (Kelvin). Il punto triplo rappresenta anche la pressione più bassa alla quale una fase liquida può esistere in equilibrio con il solido o il vapore. A pressioni inferiori a 0,00604 atm, quindi, il ghiaccio non si scioglie in un liquido all’aumentare della temperatura; il solido sublima direttamente in vapore acqueo. La sublimazione dell’acqua a bassa temperatura e pressione può essere usata per “liofilizzare” cibi e bevande. Il cibo o la bevanda viene prima raffreddato a temperature sotto lo zero e posto in un contenitore in cui la pressione viene mantenuta sotto 0,00604 atm. Poi, quando la temperatura viene aumentata, l’acqua sublima, lasciando il cibo disidratato (come quello usato dai backpackers o dagli astronauti) o la bevanda in polvere (come nel caffè liofilizzato).
Il diagramma di fase dell’acqua illustrato nella parte (b) della Figura 11.23 “Due versioni del diagramma di fase dell’acqua” mostra il confine tra ghiaccio e acqua su una scala allargata. La curva di fusione del ghiaccio degrada verso l’alto e leggermente a sinistra piuttosto che verso l’alto e a destra come nella figura 11.22 “Un tipico diagramma di fase per una sostanza che presenta tre fasi – solido, liquido e gas – e una regione supercritica”; cioè, il punto di fusione del ghiaccio diminuisce all’aumentare della pressione; a 100 MPa (987 atm), il ghiaccio fonde a -9°C. L’acqua si comporta in questo modo perché è una delle poche sostanze conosciute per le quali il solido cristallino è meno denso del liquido (altre includono antimonio e bismuto). Aumentando la pressione del ghiaccio che è in equilibrio con l’acqua a 0°C e 1 atm, si tende a spingere alcune delle molecole più vicine tra loro, diminuendo così il volume del campione. La diminuzione di volume (e il corrispondente aumento di densità) è minore per un solido o un liquido che per un gas, ma è sufficiente a sciogliere parte del ghiaccio.
Figura 11.23 Due versioni del diagramma di fase dell’acqua
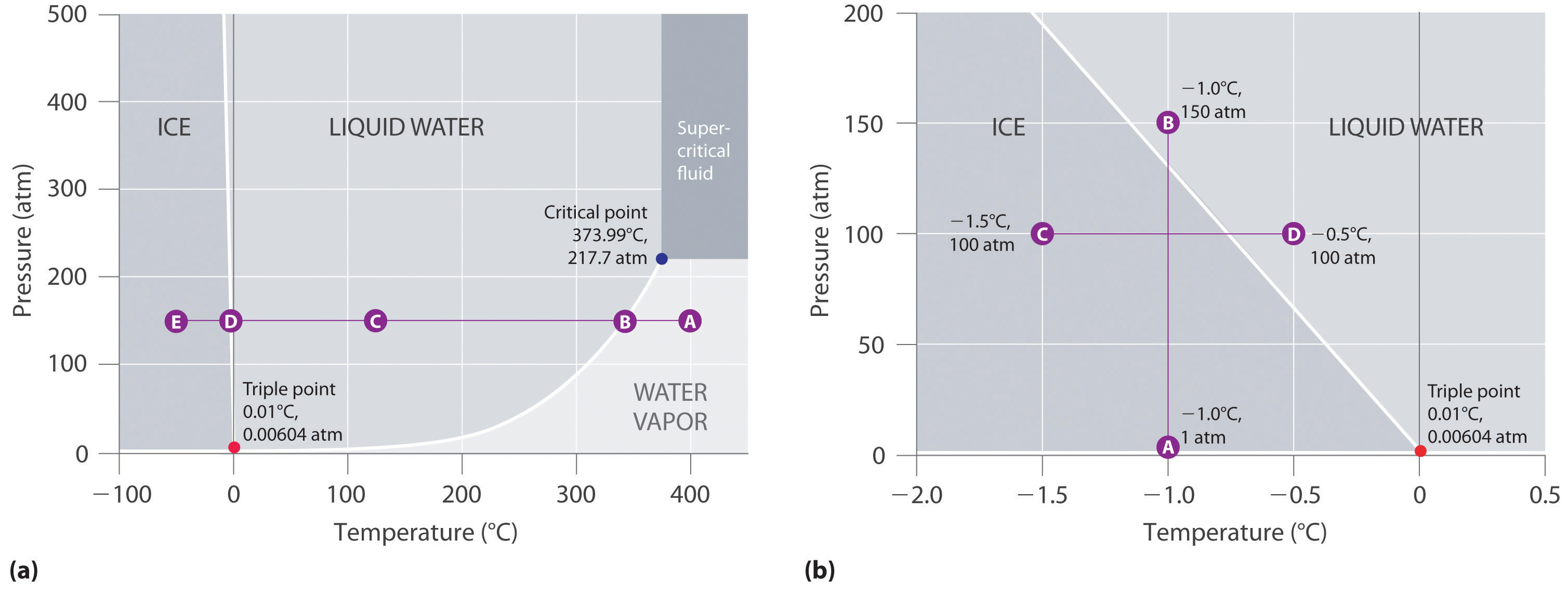
(a) In questo grafico con gli assi di temperatura e pressione lineari, il confine tra ghiaccio e acqua liquida è quasi verticale. (b) Questo grafico con una scala espansa illustra la diminuzione del punto di fusione con l’aumentare della pressione. (Le lettere si riferiscono ai punti discussi nell’esempio 10.)
Nella parte (b) della figura 11.23 “Due versioni del diagramma di fase dell’acqua”, il punto A si trova a P = 1 atm e T = -1,0°C, nella regione solida (ghiaccio) del diagramma di fase. Quando la pressione aumenta a 150 atm mentre la temperatura rimane la stessa, la linea dal punto A attraversa il confine ghiaccio/acqua fino al punto B, che si trova nella regione dell’acqua liquida. Di conseguenza, applicando una pressione di 150 atm il ghiaccio si scioglierà a -1,0°C. Abbiamo già indicato che la dipendenza dalla pressione del punto di fusione dell’acqua è di vitale importanza. Se il confine solido/liquido nel diagramma di fase dell’acqua fosse inclinato verso l’alto e verso destra piuttosto che verso sinistra, il ghiaccio sarebbe più denso dell’acqua, i cubetti di ghiaccio affonderebbero, i tubi dell’acqua non scoppierebbero quando si congelano e l’antigelo non sarebbe necessario nei motori delle automobili.
Fino a poco tempo fa, molti libri di testo descrivevano il pattinaggio su ghiaccio come possibile perché la pressione generata dalla lama del pattinatore è abbastanza alta da sciogliere il ghiaccio sotto la lama, creando così uno strato lubrificante di acqua liquida che permette alla lama di scivolare sul ghiaccio. Anche se questa spiegazione è intuitivamente soddisfacente, non è corretta, come possiamo mostrare con un semplice calcolo. Ricordiamo dal capitolo 10 “Gas” che la pressione (P) è la forza (F) applicata per unità di area (A):
Equazione 11.4
P = F A
Per calcolare la pressione che un pattinatore esercita sul ghiaccio, dobbiamo calcolare solo la forza esercitata e l’area della lama del pattino. Se assumiamo un pattinatore di 75,0 kg (165 lb), allora la forza esercitata dal pattinatore sul ghiaccio a causa della gravità è
Equazione 11.5
F = mg
dove m è la massa e g è l’accelerazione dovuta alla gravità della Terra (9,81 m/s2). Quindi la forza è
Equazione 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Se assumiamo che le lame del pattino sono 2.0 mm di larghezza e 25 cm di lunghezza, allora l’area del fondo di ogni lama è
Equazione 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Se il pattinatore sta scivolando su un piede, la pressione esercitata sul ghiaccio è
Equazione 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
La pressione è molto più bassa di quella necessaria per diminuire il punto di fusione del ghiaccio anche di 1°C, e l’esperienza indica che è possibile pattinare anche quando la temperatura è ben al di sotto dello zero. Quindi la fusione del ghiaccio indotta dalla pressione non può spiegare il basso attrito che permette ai pattinatori (e ai dischi da hockey) di scivolare. Recenti ricerche indicano che la superficie del ghiaccio, dove la schiera ordinata di molecole d’acqua incontra l’aria, consiste in uno o più strati di acqua quasi liquida. Questi strati, insieme alla fusione indotta dall’attrito quando un pattinatore spinge in avanti, sembrano spiegare sia la facilità con cui un pattinatore scivola sia il fatto che pattinare diventa più difficile al di sotto di circa -7°C, quando il numero di strati d’acqua lubrificanti della superficie diminuisce.
