Il criterio di informazione bayesiano (BIC) è un criterio di selezione del modello tra un insieme finito di modelli. Si basa, in parte, sulla funzione di verosimiglianza, ed è strettamente legato al criterio di informazione di Akaike (AIC).
Quando si adattano i modelli, è possibile aumentare la verosimiglianza aggiungendo parametri, ma così facendo si può avere un overfitting. Il BIC risolve questo problema introducendo un termine di penalità per il numero di parametri nel modello. Il termine di penalità è più grande nel BIC che nell’AIC.
BIC è stato ampiamente utilizzato per l’identificazione del modello nelle serie temporali e nella regressione lineare. Tuttavia, può essere applicato abbastanza ampiamente a qualsiasi serie di modelli basati sulla massima verosimiglianza.
Matematicamente il BIC può essere definito come-
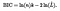

Applicazione & Interpretazione:
I modelli possono essere testati usando i corrispondenti valori BIC. Un valore BIC più basso indica termini di penalità più bassi e quindi un modello migliore.
Leggi anche le statistiche AIC.
Anche se queste due misure sono derivate da una prospettiva diversa, sono strettamente correlate. Apparentemente, l’unica differenza è che BIC considera il numero di osservazioni nella formula, cosa che AIC non fa.
Anche se BIC è sempre superiore a AIC, più basso è il valore di queste due misure, migliore è il modello.
Pratica Dataset:
Visita la nostra piattaforma di analisi e scienza dei dati, Analyttica TreasureHunt per fare pratica su set di dati reali.
Inoltre, leggi quanto segue:
Controllo di concordanza.
Filtro Kernel.
Clustering k-Means.
