Wald-teszt:

Hipotézisvizsgálat > Wald-teszt

Mi a Wald-teszt?

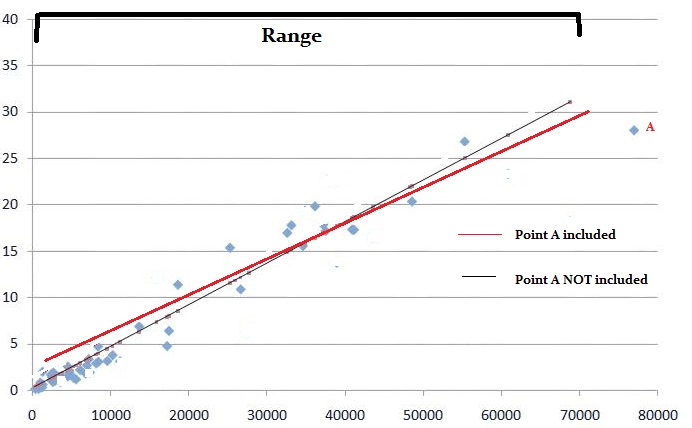
A Wald-teszt segítségével megtudhatjuk, hogy mely modellváltozók járulnak hozzá valami szignifikáns dologhoz.

A Wald-teszt (más néven Wald Chi-Squared teszt) segítségével megtudhatjuk, hogy egy modellben a magyarázó változók szignifikánsak. A “szignifikáns” azt jelenti, hogy hozzáadnak valamit a modellhez; azok a változók, amelyek nem adnak hozzá semmit, törölhetők anélkül, hogy érdemben befolyásolnák a modellt. A teszt számos különböző modellre alkalmazható, beleértve a bináris változókat vagy folytonos változókat tartalmazó modelleket is.
A teszt nullhipotézise: valamilyen paraméter = valamilyen érték. Például vizsgálhatjuk, hogy befolyásolja-e a testsúlyt a heti kétszeri egészségtelen ételek fogyasztása. A “súly” lenne a paramétered. Az érték lehet nulla (jelezve, hogy Ön szerint a súlyt nem befolyásolja az egészségtelen ételek fogyasztása). Ha a nullhipotézis elutasításra kerül, az arra utal, hogy a kérdéses változók eltávolíthatók anélkül, hogy a modell illeszkedése nagymértékben sérülne.

• Ha a Wald-teszt azt mutatja, hogy bizonyos magyarázó változók paraméterei nulla, akkor eltávolíthatja a változókat a modellből.
• Ha a teszt azt mutatja, hogy a paraméterek nem nulla, akkor a változókat be kell venni a modellbe.

A Wald-tesztről általában chi-négyzetben beszélünk, mert a mintavételi eloszlás (ahogy n a végtelenhez közelít) általában ismert. A tesztnek ezt a változatát néha Wald Chi-négyzet tesztnek nevezik, hogy megkülönböztessék a Wald Log-Lineáris Chi-négyzet teszttől, amely egy nem parametrikus változat, amely a log esélyhányadosokon alapul.

Egyeztetés más tesztekkel

A Wald-teszt a Likelihood Ratio teszt durva közelítése. Azonban egyetlen modellel is lefuttatható (az LR-teszthez legalább kettőre van szükség). Emellett szélesebb körben alkalmazható, mint az LRT: gyakran olyan helyzetekben is lefuttatható a Wald teszt, amikor más tesztet nem lehet lefuttatni.

Nagy n értékek esetén a Wald-teszt nagyjából egyenértékű a t-teszttel; mindkét teszt nagy mintanagyság esetén ugyanazokat az értékeket utasítja el. A Wald-, az LRT- és a Lagrange-szorzó-tesztek mind egyenértékűek, ahogy a mintanagyságok a végtelenhez közelednek (ezt nevezzük “aszimptotikusan egyenértékűnek”). Véges méretű minták, különösen a kisebb minták azonban valószínűleg nagyon eltérő eredményeket adnak.

Agresti (1990) azt javasolja, hogy kis mintaméretek esetén vagy ha a paraméterek nagyok, akkor a Wald-teszt helyett az LRT-t használjuk. A “kis” mintaméret körülbelül 30 alatt van.

A teszt futtatása

Segítségre van szüksége egy házi feladathoz? Nézze meg korrepetálási oldalunkat!

A Wald-teszt statisztika képlete: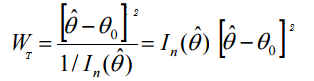

Ahol:

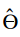• = Maximum Likelihood Estimator (MLE),
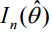• = várható Fisher információ (az MLE-nél értékelve).

A teszt alapvetően a különbségeket keresi: Θ0 – Θ. Az általános lépések a következők:

1. Keresd meg az MLE-t.
2. Keresd meg a várható Fisher-információt.
3. Értelmezd a Fisher-információt az MLE-nél.

Az MLE és a Fisher-információ kombinációjával a Wald-teszt nagyon bonyolultan működik, és nem szokták kézzel kiszámítani. Számos szoftver képes a teszt futtatására.

• Stata: használja a test parancsot.
• R: lásd a Torontói Egyetemtől származó WALD-teszt utasításokat az R számára (letölthető PDF).
• SAS: használja a TEST utasítást. A WALD az alapértelmezett, ha nincs megadva teszt.

Hivatkozás:
Agresti A. (1990) Kategorikus adatok elemzése. John Wiley and Sons, New York.

——————————————————————————

Segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez? A Chegg Study segítségével lépésről lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!